Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.
Zapisy podstawy programowej 2024 realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- objaśnia sposoby wykonywania przez komputer działań arytmetycznych i operacji logicznych;
Spis treści
- Wykonywanie operacji logicznych
- Podstawowe działania arytmetyczne na liczbach w systemie dwójkowym
- Dodawanie liczb dwójkowych
- Odejmowanie liczb dwójkowych
- Mnożenie liczb dwójkowych
- Dzielenie liczb dwójkowych
1. Wykonywanie operacji logicznych
W tradycyjnej logice dwuwartościowej posługujemy się wartościami logicznymi FAŁSZ i PRAWDA. Podstawowe operacje logiczne to: zaprzeczenie („nie”, ~), koniunkcja („i”, ∧, iloczyn logiczny) oraz alternatywa („lub”, ∨, suma logiczna). Istnieje również, rzadziej spotykana, alternatywa rozłączna („albo”, ⩒, różnica symetryczna).
Komputer, wykonując operacje logiczne na bitach, zamiast wartości FAŁSZ i PRAWDA wykorzystuje odpowiadające im odpowiednio wartości 0 i 1. Operacje logiczne w informatyce noszą nazwy angielskojęzyczne:
~ NOT
∧ AND
∨ OR
⩒ XOR lub rzadziej EOR (z ang. EXclusive OR).
W językach programowania operacje te posiadają następujące oznaczenia:
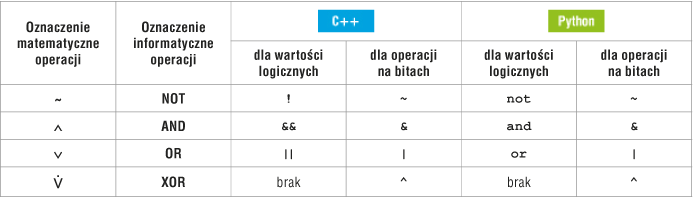
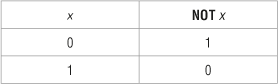
Operacja NOT jest operacją jednoargumentową. Zamienia wartość logiczną 0 na 1, a wartość logiczną 1 na 0:
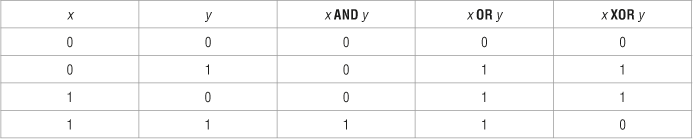
Pozostałe operacje wykonywane są na parach argumentów. Opis ich działania przedstawia tabela 3.:
Aby łatwiej zapamiętać działanie operacji, można posłużyć się następującymi regułami:
- AND daje w wyniku wartość 1 tylko wtedy, gdy obydwa argumenty mają wartość 1,
- OR daje w wyniku wartość 1, jeżeli choć jeden z argumentów ma wartość 1,
- XOR daje w wyniku wartość 1 tylko wtedy, gdy argumenty są różne.
Komputer może wykonywać operacje logiczne na wielu bitach jednocześnie (liczba bitów zależy od architektury komputera, zwykle to 8, 16, 32 bitów lub 64 bity), dokonując stosownych działań na cyfrach wielkości tego samego rzędu.
![]() Przykład 1. Obliczamy koniunkcję (iloczyn logiczny) dwóch liczb
Przykład 1. Obliczamy koniunkcję (iloczyn logiczny) dwóch liczb
Obliczymy 123 AND 37, liczba bitów = 8
123 = 011110112 (dopełniamy do 8 bitów jedną cyfrą „0” z lewej strony)
37 = 001001012 (dopełniamy do 8 bitów dwoma cyframi „0” z lewej strony)

![]() Ćwiczenie 1. Wykonujemy operacje logiczne
Ćwiczenie 1. Wykonujemy operacje logiczne
Oblicz: NOT 128, 195 AND 31, 195 OR 31, (195 XOR 31) XOR 31 dla liczby bitów = 8. Co zauważasz w ostatnim przypadku?
2. Podstawowe działania arytmetyczne na liczbach w systemie dwójkowym
W temacie A1 w książce „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III” opisaliśmy działanie procesora i podaliśmy przykład dodawania liczb przez procesor.
2.1. Dodawanie liczb dwójkowych
Aby dodać do siebie dwie liczby w systemie dziesiętnym, działamy według schematu poznanego na lekcjach matematyki w szkole podstawowej (dodawanie pisemne „w słupkach”).
![]() Ćwiczenie 2. Dodajemy liczby pisemnie „w słupkach”
Ćwiczenie 2. Dodajemy liczby pisemnie „w słupkach”
Przypomnij i omów schemat dodawania pisemnego liczb „w słupkach”.
![]() Przykład 2. Algorytm dodawania liczb
Przykład 2. Algorytm dodawania liczb
Schemat dodawania pisemnego „w słupkach” możemy zapisać w postaci sformalizowanej jako algorytm.
Zadanie: Dodaj dwie liczby naturalne n-cyfrowea i b.
Dane: Dwie liczby naturalne n-cyfrowe a i b zapisane w postaci:
an–1 an–2 … a1 a0 oraz bn–1 bn–2 … b1 b0
gdzie:
an-1, bn-1 – cyfry najbardziej znaczące,
a0, b0 – cyfry najmniej znaczące.
Wynik: Liczba c,będąca sumą liczb a i b, zapisana w postaci:
[cn] cn–1 cn–2 … c1 c0, gdzie cn lub cn-1 – cyfra najbardziej znacząca, c0 – cyfra najmniej znacząca.
Uwaga: Suma dwóch liczb może mieć o jedną cyfrę więcej od liczby cyfr większej z sumowanych liczb
Lista kroków:
- Zacznij algorytm
- Zmiennej p¸ w której będziemy pamiętać wartość przeniesienia, przypisz wartość 0: p = 0.
- Zmiennej i przypisz wartość 0: i = 0.
- Oblicz sumę pomocniczą d liczb ai, bi, p : d = ai + bi + p.
- Wyznacz wartość ci jako resztę z dzielenia d przez 10: ci = d mod 10.
- Wyznacz wartość przeniesienia p jako wynik dzielenia całkowitego d przez 10:
 p = d / 10
p = d / 10
lub
 p = d // 10.
p = d // 10. - Zwiększ i o 1: i = i + 1.
- Jeżeli i jest mniejsze od n, idź do kroku 4.
- Jeżeli p jest różne od 0, przypisz jego wartość cn: cn = p.
- Zakończ algorytm.
![]() Ćwiczenie 3. Wykonujemy algorytm dodawania liczb
Ćwiczenie 3. Wykonujemy algorytm dodawania liczb
- Zapoznaj się z algorytmem dodawania liczb przedstawionym w przykładzie 2.
- Wykonaj algorytm dla dwóch wybranych liczb czterocyfrowych.
Dla dodawania liczb w systemie dwójkowym algorytm będzie bardzo podobny – z tym, że w krokach 5. i 6. będziemy dzielić przez 2. Algorytm można zaadaptować do dodawania liczb w dowolnym systemie pozycyjnym, w krokach 5. i 6. używając do dzielenia wartości będącej podstawą danego systemu.
![]() Ćwiczenie 4. Zapisujemy algorytm dodawania dwóch liczb w systemie dwójkowym w postaci listy kroków
Ćwiczenie 4. Zapisujemy algorytm dodawania dwóch liczb w systemie dwójkowym w postaci listy kroków
Zapisz w postaci listy kroków algorytm dodawania dwóch liczb w systemie dwójkowym. Skorzystaj z przykładu 2.
![]() Ćwiczenie 5. Dodajemy liczby dwójkowe
Ćwiczenie 5. Dodajemy liczby dwójkowe
- Zamień liczby 151 i 104 na system dwójkowy.
- Dodaj otrzymane wartości dwójkowe.
- Wynik dodawania zamień na system dziesiętny. Czy otrzymana liczba to: 255?
2.2. Odejmowanie liczb dwójkowych
Odejmowanie liczb dwójkowych można wykonać na podobnej zasadzie jak dodawanie opisane wyżej. Wymagałoby to jednak istnienia w komputerze (procesorze) osobnego układu, przeznaczonego wyłącznie do wykonywania operacji odejmowania. Prościej jest wykorzystać znaną własność matematyczną:
a – b = a + (-b)
i zamiast odejmowania wykonać dodawanie liczby ujemnej. Stosowany w komputerach sposób zapisu liczb ze znakiem w kodzie uzupełnieniowym do dwóch (zobacz punkt 2.1., temat A1 w części III materiału edukacyjnego) sprawia, że zmiana znaku liczby to prosta operacja.
![]() Przykład 3. Odejmowanie liczb dwójkowych
Przykład 3. Odejmowanie liczb dwójkowych
Obliczamy wartość wyrażenia 120 – 1
120 = 011110002
-1 = 255 = 111111112
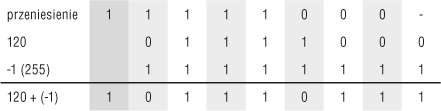
W wyniku dodawania otrzymaliśmy liczbę dwójkową 1011101112, czyli 375. Łatwo zauważyć, że 375 = 120 + 255. Jeżeli jednak pominiemy skrajny lewy bit, otrzymamy liczbę dwójkową 011101112, czyli 119. Łatwo zauważyć, że 120 – 1 = 119.
![]() Ćwiczenie 6. Odejmujemy liczby dwójkowe
Ćwiczenie 6. Odejmujemy liczby dwójkowe
Oblicz w systemie dwójkowym:
- 100 – 9
- 64 – 32
- 127 – 128
2.3. Mnożenie liczb dwójkowych
Mnożenie możemy zdefiniować jako wielokrotne dodawanie:
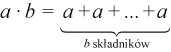
Taki sposób mnożenia byłby jednak wyjątkowo powolny w przypadku mnożenia dużych liczb, ponieważ wymagałoby wykonania nawet kilku miliardów operacji dodawania.
Komputer umożliwia szybsze wykonanie operacji mnożenia liczb całkowitych, z wykorzystaniem specjalnej operacji na bitach.
W matematyce mnożenie liczby całkowitej przez 10 (lub potęgę 10) możemy wykonać, dopisując z prawej strony tej liczby jedno 0 na każdą potęgę 10, np.:
1476 * 10 = 14760
W komputerze, operującym na liczbach w systemie dwójkowym, dodanie cyfry 0 z prawej strony odpowiada pomnożeniu liczby dwójkowej przez 2, np.:
1476 = 101110001002
1011100010002 = 2952 = 1476*2
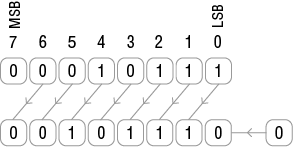
x SHL y = x * 2y,
gdzie:x – liczba,
y – liczba bitów, o które przesuwamy x.
Pokazaną na rysunku 1. operację nazywamy w informatyce przesunięciem bitowym w lewo (ang. bitshift left), MSB – najbardziej znaczący bit, LSB – najmniej znaczący bit.
![]() Ćwiczenie 7. Stosujemy przesunięcie bitowe w lewo
Ćwiczenie 7. Stosujemy przesunięcie bitowe w lewo
Oblicz w systemie dwójkowym: 512 SHL 1, 255 SHL 8.
2.4. Dzielenie liczb dwójkowych
Dzielenie możemy zdefiniować jako wielokrotne odejmowanie:
a : b = a – b – b – … – b
przy czym odejmowanie powtarzamy do osiągnięcia wartości 0 (dla dzielenia bez reszty) lub liczby mniejszej od b (dla dzielenia z resztą).
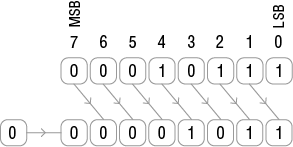
x SHR y = x : 2y,
gdzie:x – liczba,
y – liczba bitów, o które przesuwamy x.
Istnieje również operacja przesunięcia bitowego w prawo (ang. bitshift right), będąca odpowiednikiem dzielenia przez potęgę dwójki.
![]() Ćwiczenie 8. Stosujemy przesunięcie bitowe w prawo
Ćwiczenie 8. Stosujemy przesunięcie bitowe w prawo
Oblicz w systemie dwójkowym: 256 SHR 1, 255 SHR 8.

