Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.
Uwaga: Zapoznaj się wcześniej z tematem A1 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III”. Wykonaj zawarte w nim ćwiczenia i zadania.
Zapisy podstawy programowej realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
5) przedstawia sposoby reprezentowania w komputerze znaków, liczb, wartości logicznych, obrazów, dźwięków, animacji;
Spis treści
- Reprezentacja wartości logicznych
- Reprezentacja danych numerycznych w komputerze
- Reprezentacja binarna liczb ujemnych
- Reprezentacja stałopozycyjna liczb
- Reprezentacja zmiennopozycyjna liczb
- Reprezentacja znaków w komputerze
1. Reprezentacja wartości logicznych
Wartości logiczne FAŁSZ i PRAWDA w komputerze są reprezentowane przez zero i jeden. Na poziomie sprzętowym wartości 0 i 1 odpowiadają różnym poziomom fizycznym, zwykle napięcia elektrycznego, np. 0 – napięcie niskie, 1 – napięcie wysokie.
2. Reprezentacja danych numerycznych w komputerze
2.1. Reprezentacja binarna liczb ujemnych
W temacie A1 („Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III”) wyjaśniliśmy, w jaki sposób zapisać dowolną liczbę naturalną w postaci dwójkowej. Zapisanie w postaci dwójkowej liczby całkowitej ujemnej jest znacznie trudniejsze. Najbardziej oczywisty z matematycznego punktu widzenia sposób:
–147610 = –101110001002
jest, niestety, nieprzydatny, ponieważ w zapisie binarnym, stosowanym w komputerach, możemy posługiwać się tylko wartościami bitowymi: 0 i 1.
Jednym z możliwych rozwiązań tego problemu jest przeznaczenie jednego bitu liczby, np. najstarszego, na zapis znaku. Przyjmując, że na zapisanie liczby przeznaczamy 8 bitów, otrzymujemy np.:
30 = 000111102 (bit nr 7 ustawiony na 0 oznacza liczbę dodatnią),
–30 = 100111102 (bit nr 7 ustawiony na 1 oznacza liczbę ujemną).
Ten sposób reprezentacji liczb ujemnych nie jest jednak najlepszy, choćby dlatego, że stwarza dwie możliwości zapisania liczby 0:
000000002 = 0
100000002 = „–0”.
Sposób zapisu liczb ujemnych stosowany obecnie w komputerach wykorzystuje kod uzupełnieniowy do dwóch. Wartość a’ liczby a w kodzie uzupełnieniowym do dwóch wyraża się wzorem:
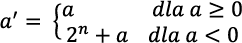 [1]
[1]gdzie:
n – liczba bitów przeznaczonych do zapisania liczby,
a – liczba do zapisania w kodzie uzupełnieniowym (–2n – 1 ≤ a < 2n – 1),
a’ – wartość liczby a w kodzie uzupełnieniowym do dwóch.
Liczbę a’, uzyskaną za pomocą wzoru [1], rozwijamy do postaci dwójkowej.
![]() Przykład 1. Wyznaczanie rozwinięcia dwójkowego liczby ujemnej w kodzie uzupełnieniowym do dwóch
Przykład 1. Wyznaczanie rozwinięcia dwójkowego liczby ujemnej w kodzie uzupełnieniowym do dwóch
a = –30, n = 8 (1 bajt)
a’ = 28 + (–30) = 256 – 30 = 226 = 111000102
Jak wynika z przykładu, liczbę dwójkową 111000102 można interpretować jako 226 lub też jako –30. Wydaje się to sprzeczne z logiką, ale logiczna struktura procesora sprawia, że taki zapis jest prawidłowy. Aby się o tym przekonać, wykonajmy działania w systemie binarnym, na przykład:
226 + 26 = 111000102 + 110102 = 111111002 = 252.
Pamiętając, że zapis liczby 226 jest taki sam, jak liczby –30, obliczamy:
–30 + 26 = –4.
Korzystając ze wzoru [1] i przyjmując n = 8, otrzymujemy:
28 + (–4) = 256 – 4 = 252 = 111111002.
Dzięki takiemu sposobowi zapisu liczb całkowitych procesor nie musi mieć dwóch osobnych układów do operacji na liczbach nieujemnych i ujemnych, co upraszcza jego budowę. Warto przy tym zauważyć, że w kodzie uzupełnieniowym do dwóch znakowi liczby odpowiada najstarszy bit. Jeżeli jest on równy 1, to liczba jest ujemna, a jeżeli jest równy 0, to liczba jest nieujemna.
![]() Ćwiczenie 1. Wyznaczamy rozwinięcia dwójkowe liczby w kodzie uzupełnieniowym do dwóch
Ćwiczenie 1. Wyznaczamy rozwinięcia dwójkowe liczby w kodzie uzupełnieniowym do dwóch
Wyznacz rozwinięcia dwójkowe liczb: –100 (n = 8), –256 (n = 16), –1000 (n = 16) w kodzie uzupełnieniowym do dwóch.
2.2. Reprezentacja stałopozycyjna liczb
Wzór podany w temacie A1 („Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III”, str. 12):
(an–1an–2…a1a0)p = an–1 · p n–1 + an–2 · p n–2 + … + a1 · p1 + a0 · p0,
gdzie:
an–1, an–2, …, a1, a0 – kolejne cyfry danej liczby,
p – podstawa systemu liczbowego,
pokazuje, w jaki sposób dokonać rozwinięcia liczby całkowitej zapisanej w systemie pozycyjnym o dowolnej podstawie. Wzór możemy zmodyfikować, tak aby można było w systemie pozycyjnym o dowolnej podstawie dokonać również rozwinięcia zapisanej w tym systemie liczby wymiernej.
Liczba a, mająca n cyfr przed przecinkiem i m cyfr po przecinku:
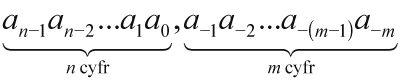
w systemie pozycyjnym o podstawie p ma rozwinięcie:
(an-1an-2…a1a0,a-1a-2…a-(m-1)a-m)p = an-1 · pn-1 + an-2 · pn-2 + … + a1 · p1 + a0 · p0 + a-1 · p-1+ a-2 · p-2 + …+ a-(m-1) · p-(m-1)+ a-m · p-m [2]
gdzie:
an–1, an–2, …, a1, a0 – kolejne cyfry liczby przed przecinkiem,
a–1, a–2, …, a–(m–1), a–m – kolejne cyfry liczby po przecinku,
p – podstawa systemu liczbowego.
![]() Przykład 2. Zapis liczby 6,6875 w systemie dwójkowym
Przykład 2. Zapis liczby 6,6875 w systemie dwójkowym
Zamiany na system dwójkowy dokonuje się, porównując liczbę z kolejnymi malejącymi potęgami dwójki. Zaczynamy od najwyższej potęgi dwójki, nie większej od danej liczby. Jeżeli liczba jest większa lub równa danej potędze, to potęga jest odejmowana od liczby i jako cyfra dwójkowa zapisywana jest jedynka. W przeciwnym razie nie wykonuje się odejmowania, a jako cyfrę dwójkową zapisuje się zero.
Porównywanie wykonujemy tak długo, aż w wyniku odejmowania otrzymamy zero lub osiągniemy żądany poziom dokładności zapisu. Przecinek w zapisie dwójkowym należy umieścić po cyfrze dwójkowej uzyskanej przy porównaniu z liczbą 1 (20).
Wynik porównania Wynik odejmowania Cyfra binarna
6,6875 > 4 (22) 2,6875 1
2,6875 > 2 (21) 0,6875 1
0,6875 < 1(20) 0,6875 0
0,6875 > 0,5 (2-1) 0,1875 1
0,1875 < 0,25 (2-2) 0,1875 0
0,1875 > 0,125 (2-3) 0,0625 1
0,0625 = 0,0625 (2-4) 0 1
Otrzymujemy:
6,6875 = 4 + 2 + 0,5 + 0,125 + 0,0625 = 22 + 21 + 2–1 + 2–3 + 2–4 = = 1 · 22 + 1 · 21 + 0 · 20 + 1 · 2– 1 + 0 · 2–2 + 1 · 2–3 + 1 · 2–4 = 110,10112
![]() Przykład 3. Nieskończone rozwinięcie dwójkowe
Przykład 3. Nieskończone rozwinięcie dwójkowe
Liczba 0,4 ma nieskończone rozwinięcie dwójkowe 0,(0110)2 = 0,011001100110…2
![]() Ćwiczenie 2. Obliczamy rozwinięcie dwójkowe liczby dziesiętnej
Ćwiczenie 2. Obliczamy rozwinięcie dwójkowe liczby dziesiętnej
Oblicz rozwinięcia dwójkowe liczb: 0,25; 4,33; 8,0001.
W praktyce zapis stałopozycyjny jest wykorzystywany stosunkowo rzadko. Pozwala on wprawdzie na zapisanie w systemie dwójkowym dowolnej liczby rzeczywistej, ale w przypadku liczb bardzo dużych lub ułamków bliskich zeru taki zapis wymaga wielu bitów. Dlatego większość komputerów korzysta ze zmiennopozycyjnej reprezentacji liczb.
2.3. Reprezentacja zmiennopozycyjna liczb
W wielu obliczeniach naukowych występują bardzo duże liczby, np.:
30! = 265252859812191058636308480000000
W zapisie naukowym podaną liczbę można zapisać w następujący sposób:
30! = 2,65253E32, tzn. 2,65253 · 1032
W podobny sposób zapisujemy liczby bliskie zeru, np.: stałą grawitacyjną
Gc = 0,0000000000667259 = 6,67259E−11, czyli 6,67259 · 10−11
Dowolną liczbę rzeczywistą a można zapisać jako:
a = m · 10c [3]
gdzie:
m – mantysa liczby,
c – cecha liczby, c jest liczbą całkowitą.
Uwaga:
Cecha i mantysa liczby występujące we wzorze [3] nie są odpowiednikami cechy i mantysy znanych z lekcji matematyki. W omawianym przypadku mantysa m jest liczbą z przedziału (–10; 10), a cecha c jest liczbą całkowitą (jak w postaci wykładniczej).
czyli 10–1 ≤ │m│ < 100, to mówimy o zapisie znormalizowanym.
![]() Ćwiczenie 3. Zapisujemy liczby w sposób znormalizowany
Ćwiczenie 3. Zapisujemy liczby w sposób znormalizowany
Zapisz w sposób znormalizowany następujące liczby:
π, 10242, 1 000 000 000.
Im więcej cyfr w mantysie, tym dokładniej zapisana jest wartość liczby. Cyfry mantysy nazywamy cyframi znaczącymi.
W zapisie dwójkowym tę samą liczbę a można zapisać jako:
a = m’ · 2c’ [4]
gdzie:
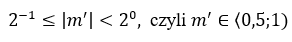
c’ jest natomiast liczbą całkowitą.
Aby liczbę a zapisać w postaci bitowej, wystarczy przekształcić m i c do postaci binarnej i zapisać przy użyciu odpowiedniej liczby bitów. Dokładny sposób zapisu określa standard IEEE 754.
Standard IEEE 754 definiuje dwa formaty:
- pojedynczej precyzji: 1 bit na znak liczby, 8 bitów na cechę liczby powiększoną o 127, 23 bity na mantysę liczby, co pozwala na zapisanie liczb z przedziału ok. ⟨-1038; 1038⟩ z dokładnością do 8 znaczących cyfr dziesiętnych:
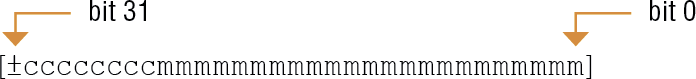
- podwójnej precyzji: 1 bit na znak liczby, 11 bitów na cechę liczby powiększoną o 1023, 52 bity na mantysę liczby, co pozwala na zapisanie liczb z przedziału ok. ⟨-1038; 1038⟩ z dokładnością do 16 znaczących cyfr dziesiętnych:
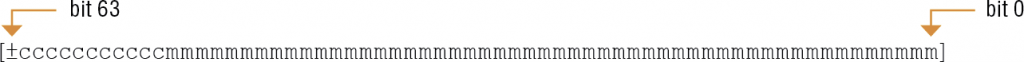
Taki sposób zapisu liczb rzeczywistych nazywamy reprezentacją zmiennopozycyjną lub zapisem zmiennoprzecinkowym.
3. Reprezentacja znaków w komputerze
W postaci dwójkowej przedstawiamy nie tylko liczby, ale również inne znaki, np. litery, znaki interpunkcyjne, znaki kontrolne (nową linię, spację). Najbardziej rozpowszechnionym sposobem kodowania liter i innych znaków alfanumerycznych jest kod ASCII (z ang. American Standard Code for Information Interchange). Każda litera czy symbol posiada w tym kodzie swój odpowiednik liczbowy z zakresu <0, 255>, (czyli zajmuje jeden bajt pamięci), np. spacja ma kod 32, znak „=” ma kod 61, znak „@” – kod 64, litera „a” – kod 97.
W programie Tablica znaków systemu Windows lub w oknie wstawiania symboli (opcja Symbol na karcie Wstawianie) edytora Microsoft Word można odnaleźć kod konkretnego znaku. W edytorze tekstu niektórym znakom przypisano klawisze skrótu. Każdy znak można też wpisać, trzymając wciśnięty lewy klawisz Alt i wpisując na klawiaturze numerycznej kod ASCII (dziesiętny) tego znaku, poprzedzony zerem.
![]() Ćwiczenie 4. Stosujemy kod ASCII do wstawiania znaków z klawiatury
Ćwiczenie 4. Stosujemy kod ASCII do wstawiania znaków z klawiatury
Korzystając z tabeli kodów ASCII dostępnej w Internecie, programu Tablica znaków lub okna wstawiania symboli edytora tekstu, odszukaj kod znaku „§”. Wprowadź go, korzystając wyłącznie z klawiatury komputera.
Opracowany w Stanach Zjednoczonych kod ASCII nie uwzględniał w chwili swojego powstania znaków charakterystycznych dla języków innych niż angielski, np. polskich liter: ą, ę, ć, ó, ł, ń, ś, ż, ź. Z chwilą pojawienia się w Polsce popularnych komputerów próbowano kilkukrotnie rozwiązać ten problem, kodując polskie znaki diakrytyczne rzadziej wykorzystywanymi kodami. Przez pewien czas w Polsce używano sześciu różnych sposobów kodowania. Ostatecznie do dzisiaj przetrwały dwa z nich: międzynarodowy ISO-8859-2 oraz wykorzystywana w systemie Windows tzw. strona kodowa 1250 (możemy więc mówić o standardzie Windows-1250).
![]() Ćwiczenie 5. Sprawdzamy kody ASCII polskich znaków
Ćwiczenie 5. Sprawdzamy kody ASCII polskich znaków
Korzystając z Internetu, sprawdź kody ASCII polskich znaków w standardach Windows-1250 i ISO-8859-2.
Następcą kodu ASCII jest standard Unicode. W standardzie tym jeden znak zajmuje dwa bajty, co pozwala na zapisanie 65536 różnych znaków. Pierwszych 256 znaków jest takich samych, jak w standardzie ASCII, pozostałe przeznaczono dla alfabetów narodowych, w tym m.in. języka arabskiego, hebrajskiego, chińskiego i japońskiego, a także różnego rodzaju znaków specjalnych (w tym emotikonów zwanych też emoji).
![]() Ćwiczenie 6. Sprawdzamy kody Unicode polskich znaków
Ćwiczenie 6. Sprawdzamy kody Unicode polskich znaków
Korzystając z Internetu, sprawdź kody Unicode polskich znaków.
![]() Ćwiczenie 7. Sprawdzamy kody Unicode emoji
Ćwiczenie 7. Sprawdzamy kody Unicode emoji
Korzystając z Internetu, sprawdź kody Unicode znaków:  ,
,  ,
,  .
.
![]() Zadania
Zadania
- Zapisz w standardzie IEEE 754 liczbę 12,75.
- Przedstaw algorytm zamiany ułamka dziesiętnego na liczbę dwójkową. Według tego algorytmu rozwiń dwójkowo liczbę 0,65.
- Napisz programy wypisujące szesnastkowo kody ASCII znaków tekstu wprowadzonego przez użytkownika. Dla zainteresowanych
- Napisz program wyznaczający postać binarną podanej liczby ze znakiem, przy wykorzystaniu podanej liczby bitów.
