Temat A5. Reprezentacja danych numerycznych w komputerze

Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.

Uwaga: Zapoznaj się wcześniej z tematem A1 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III” lub z tematem 50 z podręcznika z podręcznika „Informatyka 1-3. Podręcznik dla szkoły ponadpodstawowej. Zakres podstawowy”. Wykonaj zawarte w nim ćwiczenia i zadania.

Zapisy podstawy programowej realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

5. przedstawia sposoby reprezentowania w komputerze znaków, liczb, wartości logicznych, obrazów, dźwięków, animacji;

Spis treści

1. Reprezentacja binarna liczb ujemnych
2. Reprezentacja liczb niecałkowitych
   1. Reprezentacja stałopozycyjna liczb
   2. Reprezentacja zmiennopozycyjna liczb

1. Reprezentacja binarna liczb ujemnych

W temacie 50. z podręcznika „Informatyka 1-3. Podręcznik dla szkoły ponadpodstawowej. Zakres podstawowy” i temacie A1 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III”  wyjaśniliśmy, w jaki sposób zapisać dowolną liczbę naturalną w postaci dwójkowej (binarnej), zwanej naturalnym kodem binarnym (NKB).

Największą wartość liczby dziesiętnej (W₁₀), jaką można zapisać na n bitach, można wyznaczyć ze wzoru:

W₁₀ = 2ⁿ – 1,

np. na ośmiu bitach (n = 8) można zapisać maksymalną wartość w systemie dziesiętnym równą:

W₁₀ = 2⁸ – 1 = 256 – 1 = 255.

Aby wyznaczyć liczbę bitów n potrzebnych do zapisania wartości W w systemie dziesiętnym, należy przekształcić wzór W₁₀ = 2ⁿ – 1.

2ⁿ = W₁₀ – 1

n = log₂ (W₁₀ – 1)

Otrzymaną wartość n należy zaokrąglić w górę do najbliższej liczby naturalnej n (tzw. sufit).

Zapisanie w postaci dwójkowej liczby całkowitej ujemnej jest znacznie trudniejsze. Najbardziej oczywisty z matematycznego punktu widzenia sposób:

–1476₁₀ = –10111000100₂

jest, niestety, nieprzydatny, ponieważ w zapisie binarnym, stosowanym w komputerach, możemy posługiwać się tylko wartościami bitowymi: 0 i 1.

Aby rozwiązać ten problem, można przeznaczyć jeden bit liczby, np. najstarszy (najbardziej znaczący), na zapis znaku. Przyjmując, że na zapisanie liczby przeznaczamy 8 bitów, otrzymujemy np.:

Taka reprezentacja liczb ujemnych nie jest jednak najlepsza, choćby dlatego, że istnieją w niej dwie możliwości zapisania liczby 0:

00000000₂ = 0
10000000₂ = „–0”.

oraz suma liczb przeciwnych, w tym przypadku 30 + (-30),  na 8 bitach nie daje wszędzie wartości 0.

Sposób zapisu liczb ujemnych stosowany we wszystkich nowoczesnych komputerach wykorzystuje kod uzupełnieniowy do dwóch (U2). Wartość liczby a w kodzie uzupełnieniowym do dwóch (U2) wyraża się wzorem:

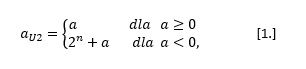
gdzie:

n – liczba bitów przeznaczonych do zapisania liczby,

a – liczba do zapisania w kodzie uzupełnieniowym (-2^n-1 ≤ a < 2^n-1),

a_U2 – wartość liczby a w kodzie uzupełnieniowym do dwóch.

Liczbę a_U2, uzyskaną za pomocą wzoru (1), rozwijamy do postaci dwójkowej.

Przykład 1. Wyznaczanie rozwinięcia dwójkowego liczby ujemnej w kodzie uzupełnieniowym do dwóch

a = –30, n = 8 (1 bajt)
a_U2 = 2⁸ + (–30) = 256 – 30 = 226 = 11100010 ₂

Jak wynika z przykładu, liczbę dwójkową 11100010₂ można interpretować jako 226 lub jako –30. Na pierwszy rzut oka wydaje się to sprzeczne ze zdrowym rozsądkiem.

Logiczna struktura procesora sprawia jednak, że taki zapis jest prawidłowy.

Na ośmiu bitach suma liczb przeciwnych, w tym przypadku -30 oraz 30, na każdej pozycji daje wartość 0.

– 30₁₀  + 30₁₀ = 11100010 _U2 + 00011110 _U2 = 1 00000000 _U2

Dzięki takiemu sposobowi zapisu liczb całkowitych procesor nie musi mieć dwóch osobnych układów do operacji na liczbach nieujemnych i ujemnych, co upraszcza jego budowę. Warto przy tym zauważyć, że w kodzie uzupełnieniowym do dwóch znakowi liczby odpowiada najbardziej znaczący bit. Jeżeli jest on równy 1, to liczba jest ujemna, a jeżeli jest równy 0, to liczba jest nieujemna.

Ćwiczenie 1. Wyznaczamy rozwinięcie dwójkowe liczb ujemnych

Wyznacz rozwinięcia dwójkowe liczb: –100 (n = 8), –256 (n = 16), –1000 (n = 16) w kodzie uzupełnieniowym do dwóch (U2).

Przykład 2. Inny sposób wyznaczania reprezentacji ujemnej całkowitej w kodzie U2

Istnieje prostszy sposób wyznaczenia reprezentacji ujemnej całkowitej w kodzie U2 na podstawie binarnej reprezentacji liczby do niej przeciwnej.

Zadanie: Wyznacz w kodzie U2 rozwinięcie liczby a = – 68 na 8 bitach wraz z bitem znaku.
Dane: binarne rozwinięcie liczby naturalnej a wraz z bitem znaku równym 0.
Wynik: binarne rozwinięcie liczby przeciwnej -a wraz z bitem znaku w kodzie U2.

Przesuwając się od strony prawej do lewej, pozostawiamy wszystkie bity równe 0 i pierwszy bit równy 1, a każdy następny bit zamieniamy na przeciwny.

2. Reprezentacja liczb niecałkowitych

2.1. Reprezentacja stałopozycyjna liczb

Reprezentacja stałopozycyjna to reprezentacja, w której na część całkowitą liczby i na jej część ułamkową przeznacza się określoną liczbę bitów. Część całkowitą oraz część ułamkową traktuje się niezależnie. Znak liczby określa bit znaku (b_z). Położenie przecinka oddzielającego część całkowitą od ułamkowej jest stałe.

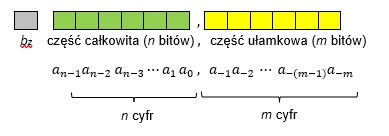
W systemie pozycyjnym o podstawie p niecałkowita liczba dodatnia:

 (a_n-1 a_n-2 … a₂ a₁ a₀ , a_-1 a_-2 … a_-(m-1) a_-m )_p

ma wartość dziesiętną równą

a_n-1 ∙ p^n-1 + a_n-2 ∙ p^n-2 + … + a₁ ∙ p¹ + a₀ ∙ p⁰ + a_-1 ∙ p^-1 + a_-2 ∙ p^-2 + … + a_-(m-1) ∙ p^-(m-1) + a_-m ∙ p^-m,

gdzie:

a_n-1 , a_n-2 , … , a₁ , a₀                          –             kolejne cyfry liczby przed przecinkiem,
a_-1 , a_-2 , … , a_-(m-1) , a_-m                     –             kolejne cyfry liczby po przecinku,
p                                                              –             podstawa systemu

Na przykład reprezentacją binarną stałopozycyjną liczby 13,625, na którą przeznaczymy po 6 bitów na część całkowitą oraz ułamkową (m = n = 6), będzie liczba:

0 001101 101000 _U2.

Aby otrzymać binarne rozwinięcie wymiernej liczby ujemnej, można posłużyć się tym samym algorytmem co w przypadku liczb całkowitych (przykład 2.).

Aby obliczyć wartość binarnej liczby wymiernej w systemie dziesiętnym, możemy posłużyć się wzorem:

gdzie:
W₁₀ – wartość liczby w systemie dziesiętnym,
b_z – bit znaku (b_z Î {0, 1}),
n – liczba bitów części całkowitej,
m – liczba bitów części ułamkowej,
a_n-1 , a_n-2 , … , a₁ , a₀ – kolejne bity liczby przed przecinkiem,
a_-1 , a_-2 , … , a_-(m-1) , a_-m – kolejne bity liczby po przecinku.

Binarną reprezentacją stałopozycyjną liczby -13,625 będzie liczba:

1 110010 011000 _U2.                              (bit znaku został pogrubiony)

Sprawdzimy poprawność wyznaczonej liczby, wykorzystując wzór [2.].

(-1) ∙ 1 ∙ 2⁶ + 1 ∙ 2¹ + 1 ∙ 2⁴ + 1 ∙ 2⁵ + 1 ∙ 2^-2 + 1 ∙ 2^-3 = -64 + 50,375 = -13,625

Przykład 3. Zapis liczby 6,6875 w systemie dwójkowym – przykład liczby mającej skończone rozwinięcie binarne

Część ułamkowa liczby ma skończone rozwinięcie binarne, jeśli mianownik ułamka jest potęgą liczby 2. Będą to więc ułamki o mianownikach: 2, 4, 8, 16, 32, 64 … etc. Część całkowitą liczby dodatniej przedstawiamy w NKB (naturalnym kodzie binarnym). Ułamek przedstawiamy jako sumę ułamków o mianownikach będących potęgami liczby 2. Na początku musimy ustalić, na ilu bitach będziemy przechowywać liczbę, zarówno jej część całkowitą, jak i ułamkową. I tak liczba 6₁₀ = 110₂, więc na jej reprezentację wystarczą 4 bity (łącznie z bitem znaku, w tym przypadku – 0, gdyż liczba jest dodatnia). Wartość 0, 6875₁₀ = 0,5₁₀ + 0,125₁₀ + 0, 0625₁₀ = 1/2 ₁₀ + 0/4₁₀ + 1/8 ₁₀ + 1/16₁₀. Zatem w części ułamkowej po przecinku będziemy mieć wartość 0, 1011. Ostatecznie otrzymamy:

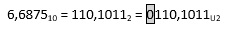
Aby znaleźć reprezentację liczby – 6, 6875, możemy postępować zgodnie z przykładem 2. Otrzymamy wówczas:

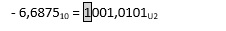
Przykład 4. Nieskończone rozwinięcie binarne

W tabeli pokazujemy znajdowanie reprezentacji binarnej ułamka 0,4.

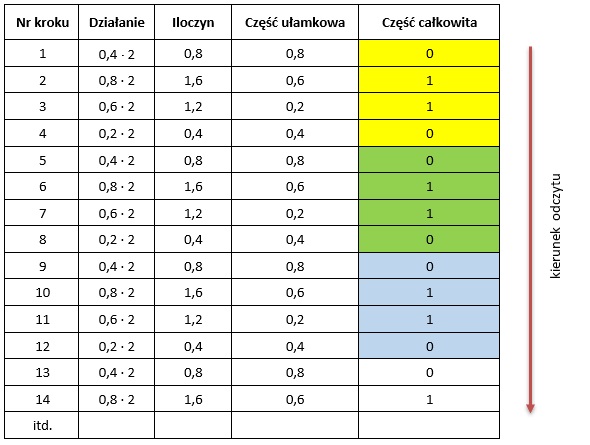
0,4₁₀ = 0,(0110)₂ = 0,011001100110 … ₂      

Ostateczna wartość reprezentacji ułamka mającego nieskończone rozwinięcie binarne zależy od liczby bitów przeznaczonych na reprezentację części ułamkowej oraz wartości dziesiętnego zaokrąglenia. Dla naszego przykładu przedstawia się to następująco:

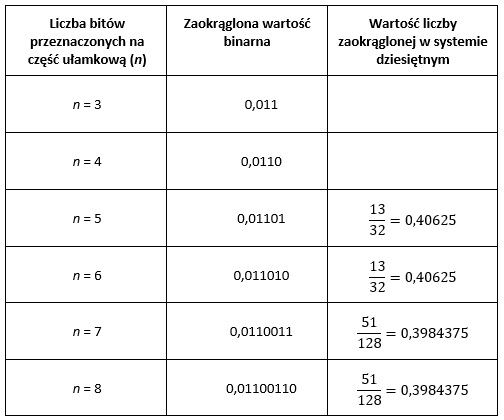
Zaokrąglenie części ułamkowej odbywa się zgodnie z następującą zasadą: jeśli pierwszą niemieszczącą się cyfrą jest zero, to odrzucamy wszystkie niemieszczące się cyfry; w przeciwnym przypadku do ostatniej pozycji zaokrąglenia dodaje się 1.

Ćwiczenie 2. Obliczamy rozwinięcia dwójkowe liczb dziesiętnych

Oblicz rozwinięcia dwójkowe liczb: 0,25; 4,33; 8,0001.

2.2. Reprezentacja zmiennopozycyjna liczb

W wielu obliczeniach naukowych występują bardzo duże liczby, np.:

30! = 265252859812191000000000000000000.

W zapisie naukowym liczbę tę można zapisać w następujący sposób:

30! = 2,65253E32, tzn. 2,65253 · 10³².

W podobny sposób zapisujemy liczby bliskie zeru, np.:
stała grawitacyjna G_c = 0,0000000000667259 = 6,67259E-11, czyli 6,67259 · 10^-11.
Dowolną liczbę rzeczywistą a można zapisać jako:

a = m · 10^c,                                                                                     [3.]

gdzie:
m – mantysa liczby,
c – cecha liczby, c jest liczbą całkowitą.

Jeżeli mantysa m liczby a należy do przedziału lewostronnie domkniętego ❬0,1; 1), czyli

1 ≤ │m│ < 10                     (ogólnie  1 ≤ │m│ < p, gdzie p – podstawa systemu),

to mówimy o zapisie znormalizowanym.            

Ćwiczenie 3.

Zapisz w sposób znormalizowany następujące liczby: π, 10242, 1 000 000 000.

W zapisie dwójkowym tę samą liczbę a można zapisać jako:

a = m · 2^c,                           [4.]

gdzie:

2^–1 ≤ │m│ < 2⁰, czyli m ∈ ❬ 0,5; 1); c jest natomiast liczbą całkowitą.
1≤ │m│ < 2 m ∈ ❬ 1; 2)

Aby liczbę a zapisać w postaci bitowej, wystarczy przekształcić m i c do postaci binarnej i zapisać przy użyciu odpowiedniej liczby bitów. Dokładny sposób zapisu określa standard IEEE 754, definiujący dwa formaty:

• pojedynczej precyzji – 1 bit na znak liczby, 8 bitów na cechę liczby powiększoną o 127 (tzw. bias), 23 bity na mantysę liczby, co pozwala na zapisanie liczb z przedziału ok. ❬-10³⁸; 10³⁸❭  z dokładnością do 8 znaczących cyfr dziesiętnych.

• podwójnej precyzji – 1 bit na znak liczby, 11 bitów na cechę liczby powiększoną o 1023 (tzw. bias), 52 bity na mantysę liczby, co pozwala na zapisanie liczb z przedziału ok. ❬-10³⁰⁸, 10³⁰⁸❭ z dokładnością do 16 znaczących cyfr dziesiętnych.

Taki sposób zapisu liczb rzeczywistych nazywamy reprezentacją zmiennopozycyjną lub zapisem zmiennoprzecinkowym.

Liczbę w tym zapisie można więc wyrazić wzorem:

x = (-1)^znak ∙ mantysa ∙ 2^cecha-bias ,

gdzie:

znak – liczba 0 dla liczby dodatniej i 1 dla liczby ujemnej,

bias – wartość przesunięcia (ang. bias)  (127 dla liczb pojedynczej precyzji; 1023 dla liczb podwójnej precyzji).

Przykład 5. Obliczanie wartości dziesiętnej liczby zmiennoprzecinkowej  pojedynczej precyzji

Dana jest następująca liczba zmiennoprzecinkowa pojedynczej precyzji:

01000011101010000000000000000000 _{(IEEE 754)}. Obliczymy jej wartość dziesiętną.

a) Kod binarny dzielimy na poszczególne pola zawierające: znak liczby, cechę oraz bity mantysy.

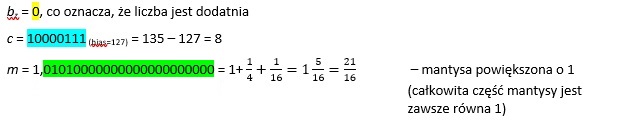
b) Obliczamy wartość:

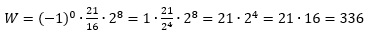
Ćwiczenie 4. Oblicz wartość dziesiętną liczby zmiennoprzecinkowej  pojedynczej precyzji 10111101010100000000000000000000.

Przykład 6. Zapisywanie liczby dziesiętnej jako liczby zmiennoprzecinkowej pojedynczej precyzji

Dana jest liczba 10,25₁₀. Zapiszemy ją jako liczbę zmiennoprzecinkową pojedynczej precyzji

a) określamy bit znaku b_z – będzie nim 0, gdyż liczba jest dodatnia,

b) przekształcamy liczbę do postaci iloczynu:

10,25 = 5,125 · 2¹ = 2,5625 · 2² = 1,28125 · 2³

Część całkowita mantysy jest równa 1, a część ułamkowa jest równa  0,28125. Wartość cechy to 3.

c) Zamieniamy część ułamkową na liczbę binarną, czyli wyznaczamy mantysę w postaci binarnej:

0,28125 * 2 = 0,5625
0,5625 * 2 = 1, 125
0,125 * 2 = 0,25
0,25 * 2 = 0,50
0,50 * 2 = 1, 00                                                      Wynik zamiany mantysy:   0,28125₁₀ = 01001₂

d) Łączymy elementy, pamiętając o tym, że wartość cechy należy powiększyć o tzw. bias (127):

e) Sprawdzamy:

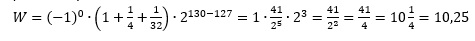
Ćwiczenie 5.

Zapisz w standardzie IEEE 754 liczbę 12,75.

Zadania

1. Na przykładzie liczby -23 przedstaw, w jaki sposób zapisuje się liczby ujemne w postaci binarnej.
2. Na przykładzie liczby 4,35 przedstaw, w jaki sposób w systemie pozycyjnym o podstawie p zapisuje się liczbę a, mającą n cyfr przed przecinkiem i m cyfr po przecinku. Przyjmij, że p = 5.
3. Wyjaśnij na wybranym przykładzie, na czym polega reprezentacja zmiennopozycyjna liczb rzeczywistych.
4. Zapisz w standardzie IEEE 754 liczbę -13,625.