Iteracyjna realizacja schematu Hornera i algorytmu Euklidesa

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

2. porównuje działanie różnych algorytmów dla wybranego problemu, analizuje algorytmy na podstawie ich gotowych implementacji;
3. w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
4. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych

II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. projektuje i tworzy programy w procesie rozwiązywania problemów, wykorzystuje w programach dobrane do algorytmów struktury danych, […]
2. sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. zapisuje za pomocą listy kroków lub pseudokodu, i implementuje w wybranym języku programowania, algorytmy poznane na wcześniejszych etapach oraz algorytmy:
   a)   algorytm Euklidesa w wersji iteracyjnej i rekurencyjnej wraz z zastosowaniami,
   h)   obliczania wartości wielomianu za pomocą schematu Hornera,

Spis treści

1. Schemat Hornera
2. Algorytm Euklidesa
   1. Wersja algorytmu Euklidesa z odejmowaniem
   2. Wersja algorytmu Euklidesa z resztą z dzielenia

1. Schemat Hornera

Schemat Hornera to algorytm do szybkiego obliczania wartości wielomianu oraz podnoszenia do potęgi, a także przeliczania na postać dziesiętną liczb zapisanych w innym systemie liczbowym.

William George Horner – brytyjski matematyk; żył w latach 1786-1837.

Przykład 1. Zastosowanie schematu Hornera do obliczania wartości wielomianu

Funkcja kwadratowa y = a₀x² + a₁x + a₂ jest wielomianem drugiego stopnia o współczynnikach a₀, a₁, a₂ (a₀, a₁, a₂, ∈ R i a₀ ≠ 0). Aby obliczyć wartość tego wielomianu, wykonujemy zwykle trzy działania mnożenia i dwa dodawania. Jeśli jednak uporządkujemy wielomian, grupując dwa pierwsze wyrazy i wyciągając wspólny czynnik x przed nawias, to otrzymamy wielomian o postaci:

y = (a₀x + a₁)x + a₂.

Aby obliczyć wartość tak zapisanego wielomianu, wystarczy wykonać dwa działania mnożenia i dwa dodawania.

Wielomian trzeciego stopnia W(x) = a₀x³ + a₁x² + a₂x + a₃ po rozpisaniu według powyższej zasady przyjmie postać: W(x) = ((a₀x + a₁)x + a₂)x + a₃.

Aby obliczyć jego wartość, wystarczy wykonać trzy działania mnożenia i trzy dodawania. Natomiast w postaci klasycznej [1] należało wykonać sześć działań mnożenia i trzy dodawania.

Uogólniając, wielomian n-tego stopnia, który ma postać:

W(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 +…+ a_n-1x + a_n         dla n ≥ 0      [1]

można uporządkować następująco:

W(x) = (…(((a₀x + a1)x + a₂)x + a₂)x +…+ a_n-1)x + a_n.

Obliczając jego wartość, będziemy wykonywać obliczenia zgodnie z zasadą kolejności wykonywania działań, poczynając od najbardziej „zagnieżdżonych” nawiasów. Za początkową wartość wielomianu należy przyjąć wartość współczynnika a₀ przy najwyższej potędze zmiennej. Za każdym razem należy aktualną wartość wielomianu pomnożyć przez x i dodać kolejny współczynnik.

Algorytm ten nazywamy schematem Hornera.

Algorytm obliczania wartości wielomianu, zwany schematem Hornera, można rozpisać następująco:
W(x) = a₀ (początkowa wartość wielomianu)
W(x) = W(x)x + a_i dla i = 1, 2, 3,…, n (iteracja)

Ćwiczenie 1. Obliczamy liczbę działań mnożenia i dzielenia w schemacie Hornera

1. Oblicz, ile razy należy wykonać działania mnożenia i dodawania, aby obliczyć wartość wielomianu W(x) z wykorzystaniem wzoru [1].
2. Zapisz rozwiązanie w pliku pod nazwą TC9_c1.

Aby obliczyć wartość wielomianu stopnia n za pomocą schematu Hornera, należy wykonać n działańmnożenia i n działań dodawania. Porównując liczbę operacji arytmetycznych wykonywanych przy wykorzystaniu wzoru [1] i schematu Hornera, widzimy, że drugi sposób jest mniej pracochłonny.

Ćwiczenie 2. Stosujemy schemat Hornera

1. Rozpisz wielomian czwartego stopnia, aby można było obliczyć jego wartość z zastosowaniem schematu Hornera.
2. Zapisz rozwiązanie w pliku pod nazwą TC9_c2.

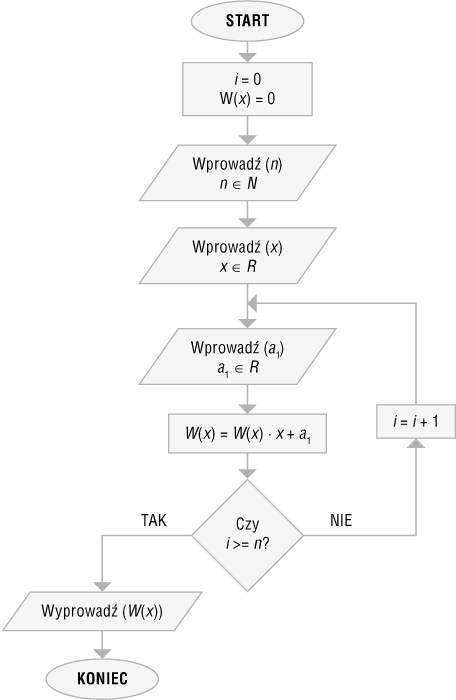
Rys. 1. Schemat blokowy algorytmu obliczania wartości wielomianu za pomocą schematu Hornera

Ćwiczenie 3. Testujemy działanie algorytmu obliczania wartości wielomianu za pomocą schematu Hornera

Przetestuj działanie algorytmu przedstawionego w postaci schematu blokowego na rysunku 1. dla wybranych danych: n = 7, a₀ = -2, a₁ = 4, a₂ = -5, a₃ = 3, a₄ = 9, a₅ = 3, a₆ = -1, a₇ = 6.

Ćwiczenie 4. Piszemy program realizujący algorytm obliczania wartości wielomianu za pomocą schematu Hornera

1. Napisz program obliczający wartości wielomianu za pomocą schematu Hornera:
   • a. dobierz odpowiednią strukturę danych do pamiętania współczynników wielomianu,
   • b. zdefiniuj trzy funkcje: wczytującą współczynniki, wypisującą na ekranie wielomian i wyprowadzającą wartość wielomianu dla danej podanej z klawiatury.
2. Zapisz program w pliku pod nazwą TC8_c4_Horner.

2. Algorytm Euklidesa

Algorytm Euklidesa służy do znajdowania największego wspólnego dzielnika (NWD) dwóch liczb naturalnych.
Największy wspólny dzielnik (NWD) dwóch lub więcej liczb naturalnych (różnych od zera) to największa liczba naturalna, przez którą dzieli się bez reszty każda z tych liczb.

2.1. Wersja algorytmu Euklidesa z odejmowaniem

Algorytm Euklidesa w wersji z odejmowaniem polega na odejmowaniu mniejszej liczby od większej i zastępowaniu większej liczby otrzymaną różnicą, dopóki większa liczba i otrzymana różnica nie będą równe.

Przykład 2. Iteracyjna realizacja algorytmu Euklidesa – wersja z odejmowaniem

Zadanie: Znajdź największy wspólny dzielnik (NWD) dla dwóch niezerowych liczb naturalnych.

Dane: Dwie niezerowe liczby naturalne: a, b.

Wynik: Wartość największego wspólnego dzielnika liczb a i b: NWD.

Lista kroków:

1. Zacznij algorytm.
2. Wprowadź wartość liczby a.
3. Wprowadź wartość liczby b.
4. Sprawdź, czy a = b: jeżeli tak, idź do kroku 7.
5. Jeżeli a > b, to
              zmiennej a przypisz wartość wyrażenia a – b;
   w przeciwnym przypadku zmiennej b przypisz wartość wyrażenia b – a.
6. Idź do kroku 4.
7. Wyprowadź wynik: NWD jest równe a.
8. Zakończ algorytm.

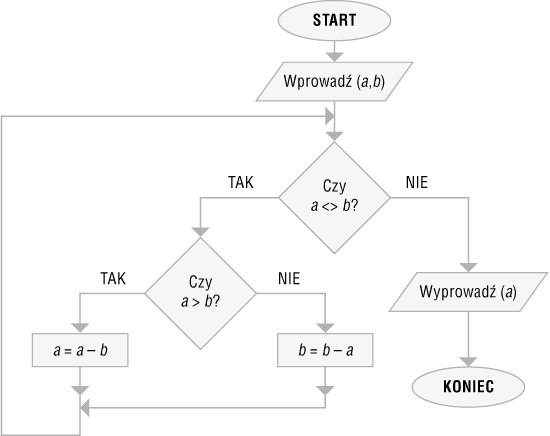
Rys. 2. Schemat blokowy algorytmu Euklidesa – wersja z odejmowaniem

Ćwiczenie 5. Piszemy program realizujący algorytm Euklidesa w wersji z odejmowaniem

1. Napisz program realizujący algorytm Euklidesa w wersji z odejmowaniem.
2. Zapisz program w pliku pod nazwą TC8_c5_Euklides1.

2.2. Wersja algorytmu Euklidesa z resztą z dzielenia

W wersji algorytmu Euklidesa z odejmowaniem odejmowanie posłużyło znalezieniu reszty z dzielenia dwóch liczb. Zamiast odejmowania możemy więc od razu zastosować dzielenie z resztą.

Przykład 3. Iteracyjna realizacja algorytmu Euklidesa – wersja z resztą z dzielenia

Wersja algorytmu z dzieleniem polega na wykonywaniu kolejnych dzieleń dwóch liczb, zastępowaniu dzielnika resztą z dzielenia i wykonywaniu obliczeń dopóki dzielnik nie osiągnie wartości 0. Wówczas dzielna jest równa NWD i algorytm się kończy. W pętli dzielną zastępujemy dzielnikiem, a dzielnik resztą z dzielenia dzielnej przez dzielnik. Zmienna k przechowuje dzielnik.

Zadanie: Znajdź największy wspólny dzielnik (NWD) dla dwóch niezerowych liczb naturalnych.

Dane: Dwie niezerowe liczby naturalne: a, b.

Wynik: Wartość największego wspólnego dzielnika liczb a i b: NWD.

Lista kroków:

1. Zacznij algorytm.
2. Wprowadź wartość liczby a.
3. Wprowadź wartość liczby b.
4. Sprawdź, czy b = 0: jeżeli tak, idź do kroku 9.
5. Zmiennej k przypisz wartość zmiennej b.
6. Zmiennej b przypisz wartość reszty z dzielenia a przez b.
7. Zmiennej a przypisz wartość zmiennej k.
8. Idź do kroku 4.
9. Wyprowadź wynik: NWD jest równe a.
10. Zakończ algorytm.

Ćwiczenie 6. Sprawdzamy liczbę operacji odejmowania (w wersji z odejmowaniem) i dzielenia (w wersji z resztą z dzielenia) w algorytmie Euklidesa

Sprawdź liczbę wykonywanych operacji odejmowania w wersji algorytmu Euklidesa z odejmowaniem i liczbę operacji dzielenia w wersji z dzieleniem dla następujących par liczb: (48, 9), (133, 49), (64, 16), (549, 145), (621, 126).

Ćwiczenie 7. Piszemy program realizujący algorytm Euklidesa w wersji z resztą z dzielenia

1. Na podstawie listy kroków podanej w przykładzie 3. napisz program realizujący algorytm Euklidesa w wersji z resztą z dzielenia.
2. Zapisz program w pliku pod nazwą TC8_c5_Euklides2.
Wskazówka: Pisząc program w językach C++ i Python, należy wykorzystać operator % w celu obliczania reszty z dzielenia, np. reszta = a % b

Zadania

1. Napisz listę kroków schematu Hornera dla wielomianu stopnia n o zadanych współczynnikach a₀, a₁, a₂, a₃, …, a_n.
2. Pokaż na przykładzie zastosowanie schematu Hornera w obliczaniu wartości wielomianu trzeciego stopnia.
3. Na podstawie listy kroków podanej w przykładzie 3. narysuj schemat blokowy algorytmu Euklidesa w wersji z resztą z dzielenia.
4. Wyjaśnij na przykładzie różnicę między wersją algorytmu Euklidesa z odejmowaniem a wersją z resztą z dzielenia.