Wyszukiwanie elementów – liniowe i przez połowienie

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. wyróżnia w problemie podproblemy i charakteryzuje: metodę połowienia, stosuje podejście zachłanne i rekurencję;
2. porównuje działanie różnych algorytmów dla wybranego problemu, analizuje algorytmy na podstawie ich gotowych implementacji;
3. w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
4. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych
   

II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. projektuje i tworzy programy w procesie rozwiązywania problemów, wykorzystuje w programach dobrane do algorytmów struktury danych, […]
2. sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. zapisuje za pomocą listy kroków lub pseudokodu, i implementuje w wybranym języku programowania, algorytmy poznane na wcześniejszych etapach oraz algorytmy:
   d)  jednoczesnego wyszukiwania elementu najmniejszego i największego,
3. objaśnia, a także porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przy tym przykłady problemów i algorytmów, w szczególności:
   c)   metodę dziel i zwyciężaj (jednoczesne znajdowanie minimum i maksimum, sortowanie przez scalanie i szybkie),

Spis treści

1. Wyszukiwanie liniowe i przez połowienie
2. Zastosowanie wyszukiwania liniowego do znajdowania najmniejszego elementu
3. Algorytm jednoczesnego znajdowania minimum i maksimum
   1. Algorytm naiwny
   2. Algorytm optymalny – metoda dziel i zwyciężaj

1. Wyszukiwanie liniowe i przez połowienie

W algorytmie wyszukiwania liniowego sprawdzamy wartość elementów zbioru po kolei, według ustalonego wcześniej porządku.

Algorytm wyszukiwania liniowego zastosujemy do znajdowania najmniejszego elementu w zbiorze.

Algorytm wyszukiwania przez połowienie jest przykładem metody dziel i zwyciężaj. Polega ona na dzieleniu przeszukiwanego zbioru (w przypadku zbioru liczb) na dwie części i zawężeniu przeszukiwania do jednej z nich. Metoda podziału pomaga w szybkim znalezieniu poszukiwanego elementu, czyli w zwycięstwie.

Nazwa „dziel i zwyciężaj” pochodzi od angielskiego sformułowania divide and conquer (parafraza słynnej łacińskiej formuły politycznej divide et impera – dziel i rządź). „Dziel” oznacza podział zadania na mniejsze części, a „zwyciężaj” – znalezienie rozwiązania (osiągnięcie sukcesu) w każdej z nich oddzielnie.

Zastosowanie metody dziel i zwyciężaj pokażemy na przykładzie algorytmu jednoczesnego znajdowania najmniejszego i największego elementu zbioru.

2. Zastosowanie wyszukiwania liniowego do znajdowania najmniejszego elementu

Algorytm znajdowania minimum (lub maksimum) ma zastosowanie w rozwiązywaniu różnych zadań, nie tylko matematycznych – np. przy wyborze najniższej ceny wśród cen tych samych produktów, przy wyborze zawodnika, który zdobył najwyższą liczbę punktów, lub ucznia, który uzyskał najwyższą średnią ocen.

Z algorytmu wyboru minimum (lub maksimum) korzysta się również w innych algorytmach, np. w algorytmach sortowania. Jeśli wiemy, jak znaleźć najmniejszy element, to łatwo uporządkujemy elementy od najmniejszego do największego.

Omówimy przykładowy algorytm znajdowania najmniejszego elementu w zbiorze (szukanie największego elementu przebiega bardzo podobnie).

Opis algorytmu: Wskazujemy dowolny element, np. pierwszy, jako najmniejszy i porównujemy go z drugim elementem. Jeśli drugi element okaże się mniejszy, to on zaczyna być traktowany jako minimum. Następnie porównujemy aktualnie najmniejszy element z trzecim elementem itd. – aż do końca ciągu elementów.

Szukanie najmniejszego elementu to typowy algorytm iteracyjny – powtarzają się w nim operacje porównywania i podstawiania.

Przykład 1. Algorytm znajdowania najmniejszego elementu z n liczb

Zadanie: Znajdź najmniejszą liczbę wśród n liczb.

Dane: Liczba naturalna n oznaczająca liczbę elementów zbioru, n liczb całkowitych wprowadzanych kolejno i zapamiętywanych w zmiennej x.

Wynik: Wartość najmniejszego elementu: najmniejszy.

Lista kroków:

1. Zacznij algorytm.
2. Wprowadź liczbę danych n: n.
3. Wprowadź pierwszą liczbę x: x.
4. Zmiennej min przypisz wartość liczby x: najmniejszy = x.
5. Wprowadź kolejną liczbę x.
6. Porównaj kolejną liczbę z najmniejszy: x < najmniejszy.
7. Jeśli kolejna liczba x jest mniejsza od minimum, przypisz jej wartość zmiennej najmniejszy: najmniejszy = x.
8. Jeśli nie jest to ostatnia liczba, wróć do kroku 5.
9. Wyprowadź wynik: najmniejszy.
10. Zakończ algorytm.

Ćwiczenie 1. Rysujemy schemat blokowy algorytmu znajdowania najmniejszego elementu

1. Narysuj schemat blokowy algorytmu znajdowania najmniejszego elementu na podstawie listy kroków przedstawionej w przykładzie 1.
2. Prześledź działanie algorytmu dla kilku różnych wartości zmiennych n i x.

Przykład 2. Definicja funkcji znajdowania minimum

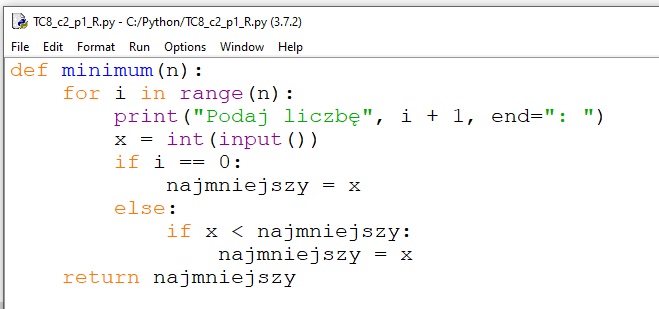
Zapisując algorytm znajdowania minimum w postaci programu, zdefiniujemy funkcję minimum z jednym parametrem n (n – liczba elementów). Funkcja będzie zwracać wartość najmniejszego elementu.

Funkcję minimum należy wywołać w programie głównym w instrukcji przypisania:

minimalna_wartosc = minimum(liczba_elementow);

Funkcję minimum należy wywołać w programie głównym w instrukcji przypisania:

minimalna_wartosc = minimum(liczba_elementow)

Ćwiczenie 2. Zapisujemy algorytm znajdowania najmniejszego elementu w postaci programu

1. Otwórz plik TC8_c2_p2.cpp lub TC8_c2_p2.py. Uzupełnij program, dodając wywołanie funkcji minimum.
2. Zapisz program w pliku pod nazwą TC8_c2_min.
3. Wykonaj zapisany w pliku program dla kilku różnych wartości zmiennych n i x.

Ćwiczenie 3. Zapisujemy algorytm znajdowania liczby największej w postaci listy kroków

1. Korzystając z przykładu 1., przedstaw (w edytorze tekstu) w postaci listy kroków algorytm znajdowania największej liczby wśród n liczb całkowitych.
2. Zapisz dokument w pliku pod nazwą TC8_c3.

Ćwiczenie 4. Zapisujemy algorytm znajdowania największego elementu w postaci programu

1. Zmodyfikuj program utworzony w ćwiczeniu 2. tak, aby znajdował maksimum z n liczb.
2. Zapisz program w pliku pod nazwą TC8_c4_max.

W programie znajdowania minimum zapisanym w ćwiczeniu 2. wszystkie wprowadzane liczby pamiętane były kolejno w zmiennej o tej samej nazwie x. Nie było konieczne zapamiętywanie wszystkich liczb w różnych zmiennych, bo zależało nam tylko na wyświetleniu najmniejszej liczby, która została zapamiętana w zmiennej najmniejszy. Podobna sytuacja występuje w programie znajdowania największego elementu (ćwiczenie 4.).

Jak pisaliśmy w temacie C6, niektóre algorytmy wymagają pamiętania wszystkich elementów zbioru zarówno w trakcie działania programu, jak również po jego zakończeniu. Aby pamiętać wszystkie elementy zbioru w oddzielnych zmiennych, zdefiniujemy funkcje, w których zapamiętamy je jako elementy tablicy (listy).

Ćwiczenie 5. Wprowadzamy elementy zbioru do tablicy (listy)

1. Zmodyfikuj programy utworzone w ćwiczeniach 2. i 4. tak, aby wprowadzane z klawiatury elementy zbioru były zapamiętywane jako elementy tablicy (C++) lub listy (Python). Liczbę elementów tablicy (listy) podaj za pomocą wcześniej zdefiniowanej stałej (LICZBA_ELEMENTOW = 10).
2. Zapisz programy w plikach pod nazwami TC8_c5_min i TC8_c5_max.

3. Algorytm jednoczesnego znajdowania minimum i maksimum

Znalezienie największego i najmniejszego elementu w zbiorze pozwala na określenie tzw. rozpiętości zbioru, czyli różnicy pomiędzy największą a najmniejszą wartością elementów występujących w danym zbiorze.

3.1. Algorytm naiwny

Algorytm naiwny szukania najmniejszego i największego elementu w zbiorze składającym się z n elementów polega na zastosowaniu algorytmu szukania minimum dla n elementów, usunięciu elementu najmniejszego ze zbioru, a następnie zastosowaniu algorytmu szukania maksimum dla zbioru składającego się z n-1 elementów (czyli pomniejszonego o element najmniejszy).

Ćwiczenie 6. Zapisujemy algorytm naiwny jednoczesnego znajdowania minimum i maksimum w postaci programu

1. Korzystając z funkcji zdefiniowanych w ćwiczeniu 5., napisz program realizujący algorytm naiwny jednoczesnego znajdowania najmniejszego i największego elementu w zbiorze.
2. Zapisz program w pliku pod nazwą TC8_c6_minmax_naiwny.
Wskazówka: Aby szukać maksimum dla zbioru pomniejszonego o element minimalny, możesz po znalezieniu minimum zamienić miejscami element minimalny z ostatnim elementem zbioru i funkcję maksimum wywołać dla liczby elementów mniejszej o 1.

3.2. Algorytm optymalny – metoda dziel i zwyciężaj

Optymalnym algorytmem jednoczesnego znajdowania najmniejszego i największego elementu jest zastosowanie metody dziel i zwyciężaj.

Opis algorytmu

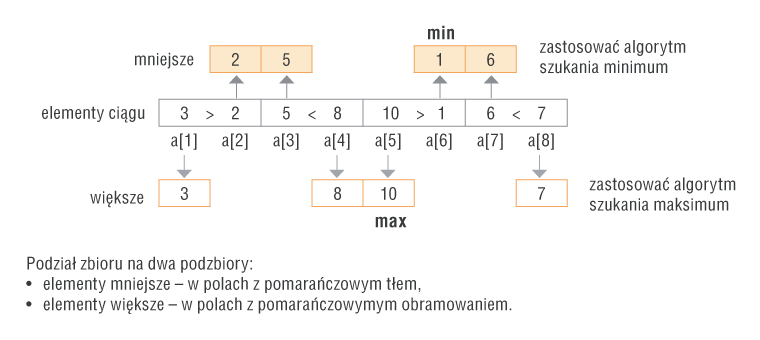
Zbiór dzielimy na dwa podzbiory w następujący sposób: porównujemy parami liczby – pierwszą z drugą, trzecią z czwartą itd. (rys. 3.). Liczby mniejsze zapisujemy w jednym podzbiorze, a większe w drugim. W pierwszym podzbiorze, korzystając z algorytmu na znalezienie minimum, znajdujemy element najmniejszy. W drugim podzbiorze, korzystając z algorytmu na znalezienie maksimum, znajdujemy element największy.

Na rysunku 1. przedstawiono przypadek, gdy liczba elementów zbioru jest parzysta (dzieli się przez 2). W przypadku nieparzystej liczby elementów ostatni element pozostanie wolny. Zapamiętuje się go w zmiennej pomocniczej i na koniec porównuje z najmniejszym i największym znalezionym elementem. W szczególnym przypadku to właśnie ten element może być minimalny bądź maksymalny.

Obliczmy liczbę porównań elementów w zbiorze n-elementowym w omówionych metodach.

W algorytmie naiwnym wykonujemy n – 1 porównań podczas znajdowania minimum i n – 2 porównań przy znajdowaniu maksimum, czyli łącznie:

porównania.

W metodzie dziel i zwyciężaj (w przypadku parzystej liczby elementów) wykonujemy najpierw porównań, aby podzielić zbiór na dwie części. W każdej części składającej się z  elementów wykonujemy porównań, czyli łącznie:

porównań.

W metodzie dziel i zwyciężaj wykonujemy mniejszą liczbę porównań niż w algorytmie naiwnym. Na przykład dla zbioru składającego się ze 100 elementów, stosując metodę dziel i zwyciężaj, wykonamy 148 porównań, a w algorytmie naiwnym – 197.

Ćwiczenie 7. Przedstawiamy algorytm jednoczesnego znajdowania minimum i maksimum na schematycznym rysunku

1. Korzystając z wybranego edytora grafiki, przedstaw na rysunku algorytm jednoczesnego znajdowania minimum i maksimum dla zbioru liczb innego niż podany na rysunku 3. Przyjmij nieparzystą liczbę elementów.
2. Ile porównań elementów wykonuje się w przypadku nieparzystej liczby elementów?
3. Zapisz rysunek w pliku pod nazwą TC8_c7.

Ćwiczenie 8. Piszemy listę kroków algorytmu jednoczesnego znajdowania minimum i maksimum z wykorzystaniem metody dziel i zwyciężaj

1. Napisz specyfikację zadania i listę kroków algorytmu jednoczesnego znajdowania minimum i maksimum z wykorzystaniem metody dziel i zwyciężaj.
2. Zapisz dokument w pliku pod nazwą TC8_c8.

Aby zapisać algorytm w językach C++ i Python, można wykorzystać w programie dwie zdefiniowane wcześniej funkcje: minimum i maksimum. Elementy zbioru trzeba wczytać do tablicy (C++) lub listy (Python). Podzbiory mniejszych i większych elementów można zapamiętywać w dwóch dodatkowo zadeklarowanych tablicach (C++) lub listach (Python). Ten sposób nie jest optymalny (duża liczba deklarowanych zmiennych), ale łatwy w wykonaniu. Można też nie deklarować dodatkowych tablic (list).

Ćwiczenie 9. Stosujemy metodę dziel i zwyciężaj do zapisania algorytmu jednoczesnego znajdowania minimum i maksimum w postaci programu

1. Napisz program realizujący algorytm jednoczesnego znajdowania najmniejszego i największego elementu, wykorzystując metodę dziel i zwyciężaj. Dobierz odpowiednie struktury danych.
2. Zapisz program w pliku pod nazwą TC8_c8_minmax_dziel_i_zwyciezaj.

Zadania

1. Na podstawie listy kroków utworzonej w ćwiczeniu 8. narysuj schemat blokowy algorytmu znajdowania największego elementu.
2. Napisz listę kroków naiwnego algorytmu jednoczesnego znajdowania elementu najmniejszego i największego.
3. Otwórz plik TC8_z3.cpp lub TC8_z3.py. W programach zdefiniowano dwie funkcje szukające minimum. Wyjaśnij, czym się od siebie różnią.
TC8_z3.cppPobierz
TC8_z3.pyPobierz
4. Napisz program, który wczytuje n-elementowy zbiór liczb całkowitych i wyprowadza różnicę między minimalnym i maksymalnym elementem, czyli tzw. rozpiętość zbioru.

Dla zainteresowanych

5. Napisz program, który wczytuje n-elementowy zbiór liczb całkowitych i wyprowadza element najbliższy wartości średniej tego zbioru.
6. Napisz program, który wczytuje tablicę (listę) dwuwymiarową N x N elementową, składającą się z liczb całkowitych i wyprowadza najmniejszy element leżący na głównej przekątnej.