Elementy analizy algorytmów

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

4. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
5. objaśnia dobrany algorytm, uzasadnia poprawność rozwiązania na wybranych przykładach danych i ocenia jego efektywność;

II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.

Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

2. sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;

Spis treści

1. Najważniejsze własności algorytmów
2. Poprawność algorytmów na przykładzie algorytmu obliczania silni
3. Skończoność algorytmów na przykładzie wybranych algorytmów

1. Najważniejsze własności algorytmów

Analiza algorytmów to złożone zagadnienie, dlatego w podręczniku omówimy tylko jej podstawowe zasady. Dociekliwych odsyłamy do dodatkowej literatury i zachęcamy do kontynuowania zdobywania wiedzy na ten temat w przyszłości na studiach informatycznych.

Aby ułatwić zrozumienie własności algorytmów, niektóre z nich omówimy, analizując przykładowe programy napisane w językach programowania C++ i Python

Tworząc algorytmy, bierzemy zazwyczaj pod uwagę ich przyszłe zastosowanie w programach. Jak pamiętamy, program komputerowy jest realizacją wybranego algorytmu (wybranych algorytmów). Algorytm powinien być zatem zapisany na tyle precyzyjnie i szczegółowo, by łatwe było zrozumienie jego działania oraz zapisanie w postaci programu, przy zastosowaniu konkretnego języka programowania.

W tym temacie omówimy poprawność i skończoność, a pozostałe własności ‒ w dalszych tematach.

2. Poprawność algorytmów na przykładzie algorytmu obliczania silni

Algorytm jest poprawny, jeżeli dla poprawnych danych daje poprawne wyniki. Dokładniej – dla dowolnej kombinacji danych wejściowych spełniających warunki początkowe algorytm wyprowadzi wyniki spełniające warunki końcowe.

Algorytm jest poprawny, jeżeli rozwiązuje problem zgodnie ze specyfikacją problemu (zadania).
Specyfikacja problemu (zadania) zawiera nie tylko opis danych i wyników, ale również opis związków, które między nimi zachodzą.

Algorytm jest całkowicie poprawny, jeśli dla wszystkich danych wejściowych spełniających warunki początkowe wyprowadzi wyniki spełniające warunki końcowe i obliczenia zostaną zakończone. Algorytm jest częściowo poprawny, jeśli wyniki obliczeń, które się skończą, są poprawne względem warunków początkowych i końcowych. W tym przypadku nie jest konieczne wykazanie, że obliczenia kończą się dla wszystkich poprawnych danych (może ich być nieskończenie wiele).

Ponadto poprawny algorytm powinien być dobrze określony i uniwersalny. Dobrze określony algorytm jest opisany w taki sposób, że występujące w nim polecenia i operacje są zrozumiałe dla użytkownika, a kolejność ich wykonania jest jednoznacznie określona.

Algorytm uniwersalny to algorytm, który umożliwia rozwiązanie dowolnego zadania z pewnej klasy zadań. Przykładem może być algorytm sortowania, który umożliwia uporządkowanie dowolnego ciągu danych.

Uniwersalność (ogólność) algorytmu wiąże się ściśle z problemem, jaki ten algorytm rozwiązuje. Chodzi o to, by algorytm umożliwiał rozwiązywanie wszystkich zadań zgodnych ze specyfikacją problemu, a różniących się jedynie danymi początkowymi.

Formalne przeprowadzenie dowodu poprawności algorytmu wymaga wiedzy matematycznej wykraczającej poza wymagania programowe dla szkół ponadpodstawowych. Trzeba bowiem dowieść, że pewne stwierdzenia zachodzą np. dla nieskończonej liczby poprawnych danych i że ciąg działań jest skończony.

Mimo że nie przeprowadzamy formalnego dowodu poprawności algorytmów, powinniśmy zawsze starać się dokładnie uzasadniać wszystkie ich kroki.

Algorytm obliczania silni liczby naturalnej n – definicja iteracyjna:

Przykład 1. Algorytm obliczania silni (realizacja iteracyjna)

Zadanie: Oblicz silnię liczby naturalnej n, stosując algorytm iteracyjny.

Dane: Dowolna liczba naturalna n.

Wynik: Wartość silni liczby naturalnej n (silnia).

Lista kroków:

1. Zacznij algorytm.
2. Wprowadź wartość liczby n.
3. Zmiennej silnia przypisz wartość 1: silnia = 1.
4. Zmiennej i przypisz wartość 1: i = 1.
5. Zmiennej silnia przypisz jej wartość pomnożoną przez i: silnia = silnia • i.
6. Powiększ wartość zmiennej i o 1: i = i + 1.
7. Jeśli i > n, to
                przejdź do kroku 8.,
   w przeciwnym wypadku przejdź do kroku 5.
8. Wyprowadź wynik: silnia.
9. Zakończ algorytm.

Ocena poprawności tego algorytmu powinna polegać na wykazaniu, że:

• jeśli dla każdej danej spełniającej warunek początkowy (n jest liczbą naturalną) w każdorazowym wykonaniu algorytmu obliczenia dochodzą do końca, to wynik (silnia) spełnia warunek końcowy (silnia = n!);
• dla wszystkich danych spełniających warunek początkowy obliczenia w algorytmie kończą się.

Formalny dowód poprawności algorytmu obliczania silni pominiemy. Można jednak dokonać kilku obserwacji:

1. Algorytm daje poprawny wynik dla n = 0, n = 1 i n = 2. Stosując rozumowanie indukcyjne, można wywnioskować, że będzie dawał poprawne wyniki także dla n > 2.
2. Warunkiem zakończenia obliczeń jest i > n. Dla n = 0 i n = 1 warunek ten jest spełniony już przy pierwszym wykonaniu kroku 7. Dla n >= 2 będzie on również spełniony, ponieważ jeśli w kroku 7. i <= n, to następuje przejście do kroku 5. Ostatecznie więc po pewnej liczbie kroków algorytmu i przyjmie wartość większą od n, a wtedy nastąpi przejście do kroku 8. i zakończenie algorytmu.

Biorąc pod uwagę te obserwacje, można wywnioskować, że algorytm jest poprawny. Zaznaczamy jednak, że z formalnego punktu widzenia nie jest to dowód na poprawność algorytmu.

Często bardziej od poprawności algorytmu interesuje nas poprawność programu realizującego ten algorytm. Zwracamy jednak uwagę, że ten sam algorytm można zapisać w języku programowania na kilka sposobów, niekoniecznie poprawnych.

Istotne są dwa rodzaje błędów, jakie mogą wystąpić w programie: błędy kompilacji (składniowe) i logiczne. Przyczyną powstania błędów logicznych może być błędne użycie instrukcji programu. Błąd logiczny powoduje, że nie dla wszystkich poprawnych danych program generuje poprawne wyniki. Wykrycie błędów logicznych nie jest łatwe. W tym celu programy poddaje się testowaniu, polegającemu na przykład na sprawdzeniu, czy dla określonych danych program generuje określone wyniki.

Przykład 2. Program obliczający wartość silni liczby naturalnej n

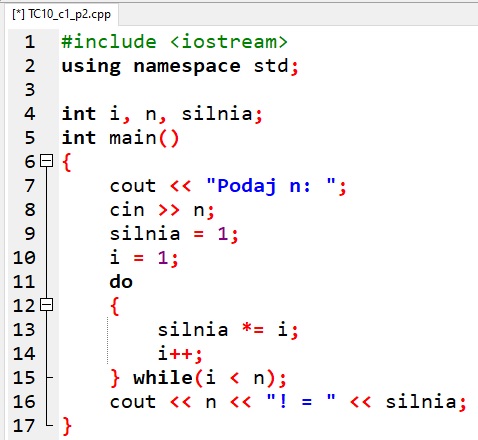
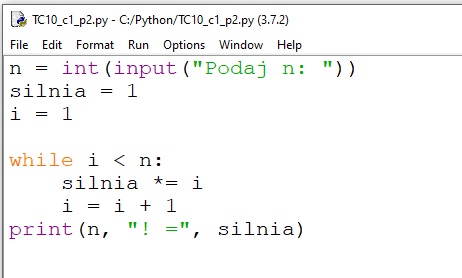
Programy zapisane w językach C++ i Python i pokazane na rysunkach są poprawnymi realizacjami algorytmu podanego w przykładzie 1, choć nie jedynymi.

Wystarczy jednak zmienić warunek i <= n na i < n w instrukcji do ... while (C++) i w instrukcji while (Python), aby dany program przestał działać poprawnie. Błędne działanie programu jest tutaj wynikiem błędu logicznego.

Uwaga: O ograniczeniach wynikających z właściwości arytmetyki komputera napiszemy w dalszych tematach.

Ćwiczenie 1. Sprawdzamy poprawność programu

1. Otwórz plik TC10_c1_p2.cpp lubTC10_c1_p2.py.
2. Przeanalizuj poprawność programu – uruchom go i sprawdź, czy wyniki jego działania jest zgodny z oczekiwaniami.
3. Popraw program i zapisz plik pod tą samą nazwą. Uruchom ponownie.

W programach z przykładu 2. algorytm obliczania silni zapisaliśmy, stosując instrukcję do … while (C++) i odpowiednio while (Python). Jednak inicjalizacja zmiennej i oraz dodawanie do niej jedynki na koniec iteracji są okazją do popełnienia dodatkowego błędu Aby tego uniknąć lepiej zastosować pętlę for, zwłaszcza że również liczba danych (n) jest z góry określona, bo wprowadzamy ją z klawiatury po uruchomieniu programu. Zatem w tym przypadku czytelniejsze i zwięźlejsze jest zastosowanie pętli for.

Ćwiczenie 2. Zapisujemy algorytm obliczania silni z użyciem pętli for

1. Otwórz plik TC10_c1_p2.cpp lubTC10_c1_p2.py zapisany w ćwiczeniu1. Zastosuj w programie pętlę for zamiast do … while (C++) i odpowiednio while (Python). Zapisz program w pliku pod nazwą TC10_c2_for.
2. Uruchom program i sprawdź, czy jest poprawny (czy wyniki jego działania są zgodne z oczekiwaniami).

3. Skończoność algorytmów na przykładzie wybranych algorytmów

Jednym z warunków poprawności algorytmu jest jego skończoność.

Algorytm jest skończony, jeżeli gwarantuje wyznaczenie wyniku w skończonej liczbie kroków.

Algorytm, który nie jest skończony, nie może zostać uznany za poprawny, bowiem nigdy nie spowoduje wyznaczenia poprawnego wyniku. Powodem nieskończonego działania algorytmu może być np. błędnie określony warunek zakończenia iteracji.

Algorytm powinien być skończony dla wszystkich danych wejściowych, to znaczy, że żadna ich kombinacja, dopuszczona przez specyfikację problemu, nie powinna powodować sytuacji, w której algorytm się nie kończy.

Przykład 3. Błędny algorytm wypisywania kolejnych liczb nieparzystych

Zadanie: Wypisz kolejne dodatnie liczby nieparzyste mniejsze od n.

Dane: Dowolna liczba naturalna n.

Wynik: Wszystkie dodatnie liczby nieparzyste mniejsze od n.

Lista kroków:

1. Zacznij algorytm.
2. Wprowadź wartość liczby n.
3. Zmiennej i przypisz wartość 1: i = 1.
4. Jeżeli i = n, przejdź do kroku 8.
5. Wyprowadź liczbę nieparzystą: i.
6. Zwiększ wartość zmiennej i o 2: i = i + 2.
7. Przejdź do kroku 4.
8. Zakończ algorytm.

Uwagi: Algorytm ten jest skończony dla każdego n nieparzystego. Jeżeli jednak podane zostanie n parzyste, to algorytm się nie zakończy. Dzieje się tak, ponieważ wartością początkową i jest 1, a za każdym razem i jest zwiększane o 2, a zatem i nigdy nie będzie parzyste. W konsekwencji warunek i = n nigdy nie będzie spełniony. Rozwiązaniem problemu jest zmiana warunku w kroku 4. na i ≥ n.

Ćwiczenie 3. Sprawdzamy skończoność programu

1. Utwórz program na podstawie listy kroków algorytmu wypisywania kolejnych liczb nieparzystych (przykład 3.). Zapisz program w pliku pod nazwą TC10_c3_p3_ns. Co zauważasz?
2. Popraw listę kroków algorytmu zgodnie z uwagami podanymi w przykładzie 3. Na podstawie poprawionej listy zmodyfikuj odpowiednio program i zapisz w pliku pod nazwą TC10_c3_p3_s. Jak teraz działa program? Uzasadnij odpowiedź.

Może się również zdarzyć, że program realizujący algorytm skończony nie zakończy się. Wynika to z właściwości arytmetyki komputerowej, gdy w algorytmie sprawdzany jest warunek dokładnej równości obliczanych wielkości.

Problem zgodności otrzymanych wyników z dokładnymi wartościami pochodzącymi z obliczeń matematycznych wynika z faktu, że komputer niektóre obliczenia są wykonywane na liczbach przybliżonych. Różnice mogą wynikać z błędów zaokrągleń.

Przykład 4. Program wypisujący wartości funkcji cosinus dla całkowitych wielokrotności kąta 10° z przedziału <0°; 90°>

Zadaniem programu jest wypisywanie cosinusów kątów od 0° do 90°. Pętla kończy się, kiedy wartość cosinusa kąta wyniesie 0.

Z matematycznego punktu widzenia jest to warunek poprawny, ponieważ cosinus kąta o mierze 90° jest równy 0. W programie wartości kąta zmieniają się co 10°, poczynając od 0°. Wartość kąta osiągnie 90° w dziesiątym wykonaniu pętli lub do ... while (C++) lub while (Python). W praktyce jednak program ten nie zakończy się, ponieważ w arytmetyce komputerowej cosinus 90° jest liczbą bardzo bliską 0, ale nie równą 0.

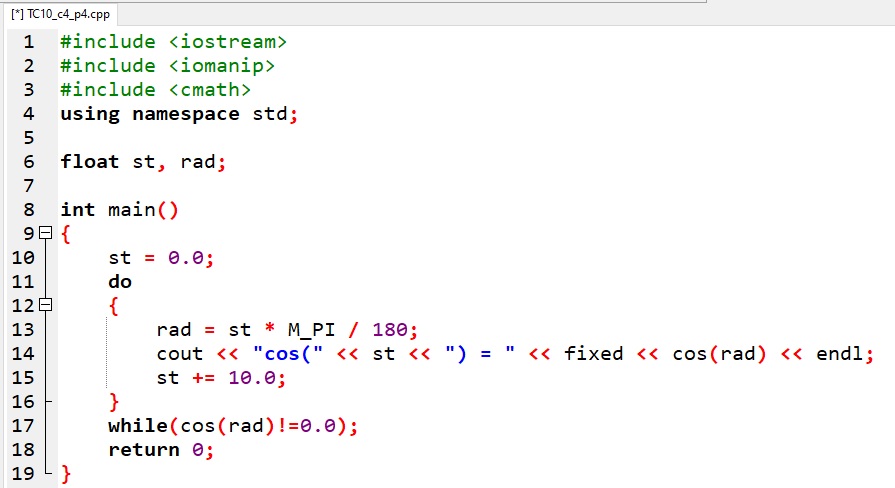
Uwaga: Wartości cosinusów są liczbami zmiennoprzecinkowymi. Użyty w programie (w wierszu 14.) manipulator fixed powoduje wyświetlanie wyników (wartości cosinusów) w notacji stałoprzecinkowej (bez części wykładniczej), a manipulator setprecision(5) – wyświetlanie liczb z pięcioma miejscami po przecinku (tu: w języku C++ po kropce dziesiętnej).

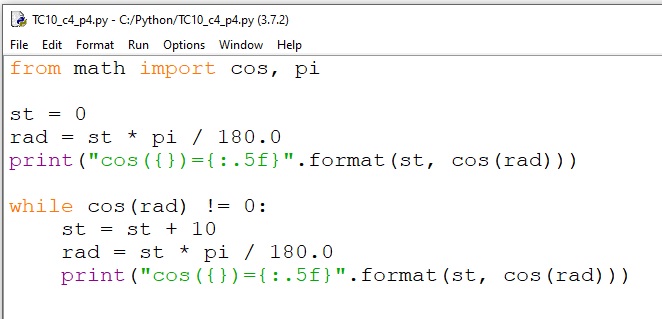
Uwaga: W programie używamy metody format. Zmienna st jest zawsze całkowita i jest wstawiana z domyślnym formatowaniem w miejscu pierwszych nawiasów klamrowych. Wartości cosinusów są liczbami zmiennoprzecinkowymi.

Domyślnie liczby zmiennoprzecinkowe wyświetlane są w sposób mało czytelny, dlatego zastosowaliśmy zapis :.5f, który powoduje wyświetlanie wyników (wartości cosinusów) zawsze z pięcioma miejscami po przecinku (tu: po kropce dziesiętnej).

Ćwiczenie 4. Modyfikujemy program, aby działał poprawnie

1. Otwórz plik TC10_c4_p4.cpp lub TC10_c4_p4.py. Uruchom program.
2. Zmodyfikuj wybrany program tak, aby działał poprawnie. Zastanów się, jak najlepiej sformułować warunek w pętli do … while (C++) lub w pętli while (Python).

Wskazówki: Aby zatrzymać zapętlony program, można nacisnąć klawisze Ctrl + C.

W dalszych tematach omówimy algorytm znajdowania miejsca zerowego funkcji metodą połowienia przedziału. W przypadku gdy założona przez użytkownika dokładność otrzymanego wyniku przekroczy możliwości arytmetyki komputerowej, algorytm ten nie zakończy się. Podobny problem występuje w algorytmie wyznaczania pierwiastka kwadratowego.

Zadania

1. Narysuj schemat blokowy algorytmu obliczania silni.
2. Zdefiniuj iteracyjną wersję funkcji silnia z jednym parametrem n zwracającą wartość silni dla n. W funkcji zastosuj pętle for. Wywołaj funkcję w programie głównym.
3. Uzasadnij skończoność algorytmu znajdowania największego wspólnego dzielnika (NWD) dwóch liczb naturalnych.
4. Oblicz liczbę operacji porównania w algorytmie wyboru minimum z tablicy zawierającej n losowo uporządkowanych liczb.

Dla zainteresowanych

5. Wymyśl zadanie (problem), napisz specyfikację zadania, listę kroków i program realizujący to zadanie. Prześlij program koledze lub koleżance, aby sprawdzili jego poprawność.
6. Wymyśl zadanie (problem), napisz specyfikację zadania, listę kroków i program realizujący to zadanie. Prześlij program koledze lub koleżance, aby sprawdzili jego skończoność.
7. W języku Python do obliczenia silni liczby naturalnej n można użyć funkcji factorial() z biblioteki math. Napisz program wyświetlający na ekranie wartość silni liczby n wprowadzanej z klawiatury, wykorzystując tę funkcję.