Rekurencyjne tworzenie fraktali

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1) wyróżnia w problemie podproblemy i charakteryzuje: metodę połowienia, podejście zachłanne i rekurencję,
4) do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1) zapisuje za pomocą listy kroków lub pseudokodu i implementuje w wybranym języku programowania algorytmy poznane na wcześniejszych etapach oraz algorytmy:
    j) rekurencyjnego tworzenia fraktali;
I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
3) objaśnia oraz porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przykłady problemów i algorytmów, w szczególności:
    b) rekurencję (do generowania ciągów liczb, potęgowania, sortowania liczb, generowania fraktali),

Spis treści

1. Krzywa Kocha i płatek Kocha
2. Trójkąt Sierpińskiego i dywan Sierpińskiego
   1. Trójkąt Sierpińskiego
   2. Implementacja rekurencyjnego tworzenia trójkąta Sierpińskiego w językach C++ i Python
   3. Dywan Sierpińskiego
   4. „Gra w chaos”
3. Fraktal Mandelbrota

1. Krzywa Kocha i płatek Kocha

Ćwiczenie 1. Przypominamy informacje o płatku Kocha

Przypomnij definicję fraktala z punktu 4. tematu „Stosowanie wybranych funkcji w realizacji algorytmów i fraktali w arkuszu kalkulacyjnym”oraz podane tam informacje o płatku Kocha.

Krzywa Kocha to obiekt geometryczny powstający w następujący sposób:

1. Narysuj odcinek o długości d.
2. Podziel odcinek na trzy równe części o długości d/3 każda.
3. Środkową część odcinka zastąp dwoma odcinkami o długości d/3 ułożonymi tak, by tworzyły trójkąt równoboczny z usuniętym odcinkiem.
4. Powtórz kroki 2-3 dla każdego otrzymanego odcinka.

Rys. 1. Trzy pierwsze iteracje krzywej Kocha

Aby narysować krzywą Kocha, można skorzystać z programu Inkscape (patrz temat „Więcej o tworzeniu i edytowaniu obrazów w programie Inkscape”).

Program Inkscape posiada generator fraktali, tzw. L-systemów, dostępny w menu Efekty po wybraniu opcji Renderowanie/L-system. Krzywą Kocha można narysować, ustalając parametry takie jak na rys. 2.

Parametry L-systemów to:

• aksjomat to krok początkowy;
• reguła określa, w jaki sposób należy dokonać rekurencyjnej zamiany elementów rysunku. W opisie reguły stosować można symbole odpowiadające do pewnego stopnia grafice żółwia w języku Python (grafikę żółwia w języku Python omawiamy w podręczniku „Teraz bajty (3D). Informatyka dla szkoły podstawowej. Klasa 7”i nawiązujemy do niejw podręczniku do klasy 8 „Teraz bajty (3D). Informatyka dla szkoły podstawowej. Klasa 8”):
  • litery A-F – rysowanie odcinka do przodu od aktualnej pozycji wirtualnego „żółwia”,
  • litery G-L – przesunięcie wirtualnego „żółwia” do przodu bez rysowania,
  • minus (–) – obrót w lewo o zadany kąt,
  • plus (+) – obrót w prawo o zadany kąt;
• kolejność to liczba iteracji procesu.

Długość odcinka i wielkość kąta obrotu „żółwia” ustala się w okienku generatora L-systemów.

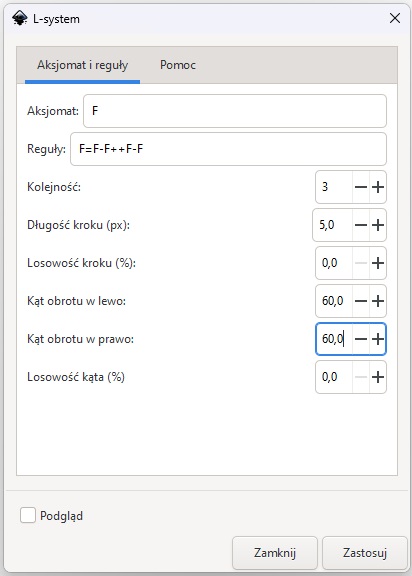
Rys. 2a. Parametry generatora L-systemów programu Inkscape do wygenerowania krzywej Kocha

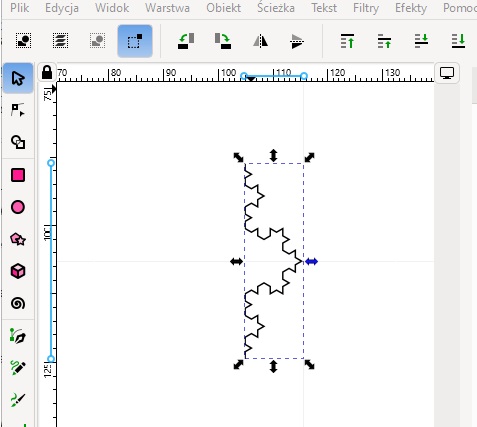
Rys. 2b. Krzywa Kocha wygenerowana w programie Inkscape według parametrów z rysunku 2a

Aby narysować płatek Kocha, należy zachować regułę rysowania krzywej Kocha i zmienić aksjomat na F++F++F (co oznacza narysowanie trzech krzywych Kocha obróconych względem siebie o 120° każda).

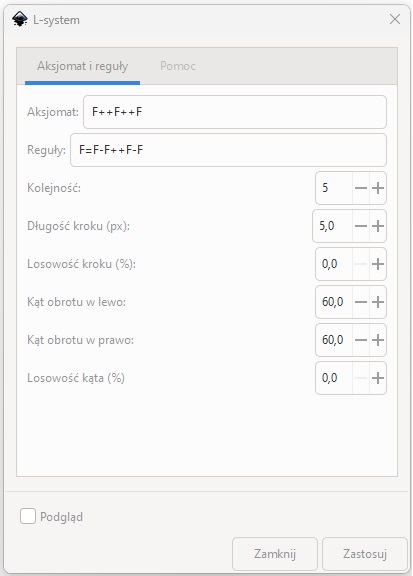
Rys. 3. Parametry generatora L-systemów programu Inkscape do wygenerowania płatka Kocha.

Rys. 4. Cztery iteracje płatka Kocha

Ćwiczenie 2. Generujemy fraktale w programie Inkscape

1. Uruchom program Inkscape.
2. Narysuj krzywą Kocha, korzystając z opisu i rysunków 2a i 2b.
3. W programie Inkscape utwórz obrazy przedstawiające cztery iteracje płatka Kocha (rys. 4.). Objaśnij regułę: F-F++F-F. Jakie parametry w oknie L-system (rys. 3.) należy zmieniać, aby narysować kolejny fraktal??

2. Trójkąt Sierpińskiego i dywan Sierpińskiego

2.1.  Trójkąt Sierpińskiego

Aby narysować trójkąt Sierpińskiego, należy postępować następująco:

1. Narysuj trójkąt równoboczny o boku długości a.
2. Podziel trójkąt na cztery trójkąty równoboczne o boku długości a/2 każdy.
3. Usuń środkowy trójkąt.
4. Powtórz kroki 2-3.

Cztery pierwsze iteracje trójkąta Sierpińskiego pokazano na rysunku 5. Po kolejnych iteracjach, zależnie od ich liczby, uzyskujemy figurę podobną do przedstawionej na rys. 6.

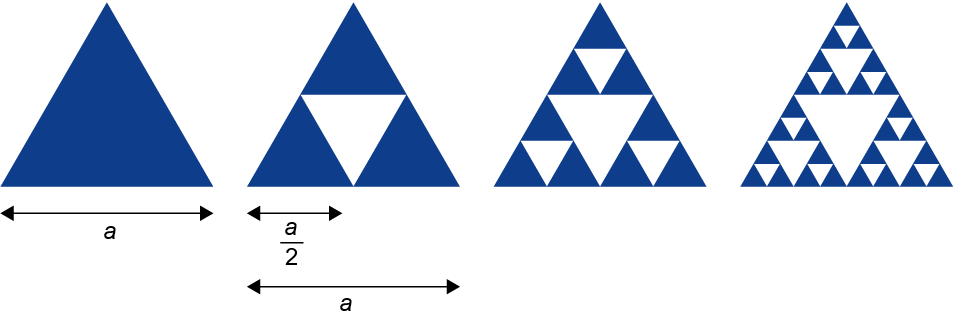
Rys. 5. Trzy pierwsze iteracje trójkąta Sierpińskiego

Rys. 6. Trójkąt Sierpińskiego

Aby narysować trójkąt Sierpińskiego w programie Inkscape, należy:

1. Narysować trójkąt równoboczny za pomocą narzędzia Gwiazda i ustawić go podstawą równolegle do osi X.
2. Zmniejszyć trójkąt o połowę, a następnie skopiować i wkleić dwa razy, kopie układając tak, by stykały się wierzchołkami ze sobą i zmniejszonym trójkątem.
3. Zaznaczyć uzyskany obiekt i zgrupować (opcja Obiekt/Grupuj).
4. Powtórzyć kroki 2-3.

Figurę przypominającą trójkąt Sierpińskiego można uzyskać również za pomocą wspomnianego już generatora L-systemów, korzystając z następujących parametrów

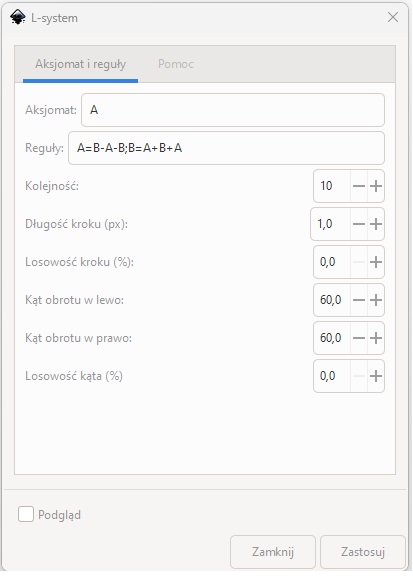
Rys. 7. Parametry generatora L-systemów programu Inkscape do wygenerowania figury przypominającej trójkąt Sierpińskiego

Ćwiczenie 3. Tworzymy trójkąt Sierpińskiego w programie Inkscape

Narysuj w programie Inkscape trójkąt Sierpińskiego.

2.2. Implementacja rekurencyjnego tworzenia trójkąta Sierpińskiego w językach C++ i Python

Standardowe biblioteki języka C++ nie zawierają komponentów do obsługi grafiki ekranowej, dlatego nie jest możliwe napisanie programu rysującego fraktal bez użycia dodatkowej, niestandardowej biblioteki. Możemy jednak napisać w języku C++ program realizujący algorytm rekurencyjnego tworzenia fraktala bez użycia tych bibliotek. W przykładzie 1. pokazujemy realizację algorytmu rekurencyjnego tworzenia trójkąta Sierpińskiego, w której fraktal zostanie „narysowany” za pomocą znaków ASCII – gwiazdek „*”.

Przykład 1. Realizacja algorytmu rekurencyjnego tworzenia trójkąta Sierpińskiego w języku C++

W programie w języku C++ „ekranem” będzie tablica dwuwymiarowa o nazwie kanwa[], której elementami będą znaki. Pierwszy indeks tej tablicy odpowiada współrzędnej Y „ekranu”, a drugi indeks – współrzędnej X. Każda komórka tablicy to jeden „piksel” naszego „ekranu”. „Rysowanie” trójkąta Sierpińskiego realizujemy w funkcji trojkatSierpinskiego(), której parametrami są współrzędne prawego dolnego rogu trójkąta (parametry x i y) oraz długość boku (parametr rozmiar). Jeżeli długość boku jest równa 1, to jest koniec rekurencji (nie da się narysować mniejszego trójkąta) i na zadanej pozycji tablicy wstawiamy znak „*” („rysujemy piksel”). W przeciwnym razie, funkcja wywołuje trzy razy samą siebie, z odpowiednimi współrzędnymi i połową długości, w ten sposób rekurencyjnie tworząc kolejne, mniejsze trójkąty.

Z podręcznika „Teraz bajty (3D). Informatyka dla szkoły podstawowej. Klasa 7” (temat 14.) i podręcznika „Teraz bajty (3D). Informatyka dla szkoły podstawowej. Klasa 8” (tematy 5. i 9.) dowiedzieliśmy się, że w bibliotece standardowej języka Python jest umieszczony moduł turtle. Funkcje tego modułu możemy wykorzystać także do narysowania trójkąta Sierpińskiego w języku Python.

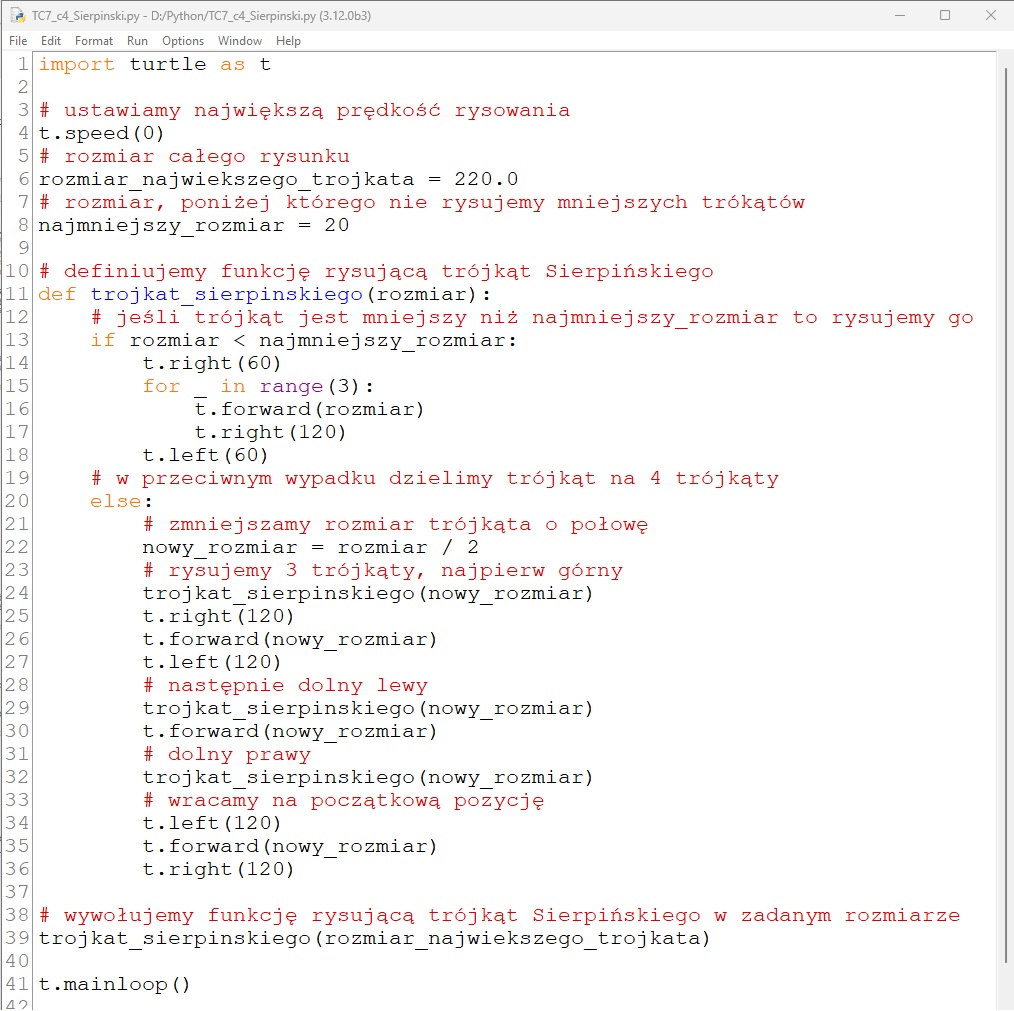
Przykład 2. Realizacja algorytmu rekurencyjnego tworzenia trójkąta Sierpińskiego w języku Python

Funkcja trojkat_sierpinskiego() rysuje trójkąt, gdy zadany rozmiar jest mniejszy niż rozmiar graniczny. W przeciwnym wypadku funkcja wywołuje samą siebie, aby narysować trzy mniejsze trójkąty. Należy zwrócić uwagę na to, że w każdym wypadku po rysowaniu „żółw” wraca na początkową pozycję.

Ćwiczenie 4. Analizujemy program rekurencyjnego tworzenia trójkąta Sierpińskiego

1. Otwórz plik TC7_c4_Sierpinski.cpp lub TC7_c4_Sierpinski.py. Uruchom program.
2. Zapoznaj się z kodem programu. Przeanalizuj wstawione do kodu komentarze. Objaśnij działanie poszczególnych funkcji programu. Jakie struktury danych użyto w programie i dlaczego? Wskaż miejsce rekurencyjnego wywołania funkcji trojkatSierpinskiego() (C++)  lub funkcji trojkat_sierpinskiego() (Python).

2.3. Dywan Sierpińskiego

Rys. 8. Dywan Sierpińskiego

Ćwiczenie 5. Opisujemy w krokach tworzenie dywanu Sierpińskiego

Opisz w krokach algorytm tworzenia dywanu Sierpińskiego.

Ćwiczenie 6. Tworzymy dywan Sierpińskiego w programie Inkscape

Narysuj kilka pierwszych iteracji dywanu Sierpińskiego w programie Inkscape.

2.4. „Gra w chaos”

Trójkąt Sierpińskiego jest obiektem deterministycznym, tzn. z góry wiadomo, jaki powinien być jego ostateczny kształt po określonej liczbie iteracji. Okazuje się jednak, że obiekt przypominający trójkąt Sierpińskiego uzyskać można w wyniku procesu losowego – jako „grę w chaos”.

Ćwiczenie 7. Realizujemy „Grę w chaos” w arkuszu kalkulacyjnym

1. W temacie „Stosowanie wybranych funkcji w realizacji algorytmów i fraktali w arkuszu kalkulacyjnym” opisaliśmy, na czym polega „gra w chaos” i pokazaliśmy realizację tego algorytmu w arkuszu kalkulacyjnym. Przypomnij sobie sposób wykonania algorytmu „gry w chaos”.
2. Otwórz plik TB1_c1_p6_Sierpinski.xls. Przeanalizuj zastosowane w tym rozwiązaniu formuły.
   Wskazówka: Naciskając klawisz F9, wylosujesz nowy zestaw liczb.

3. Fraktal Mandelbrota

Nazwa fraktala pochodzi od nazwiska jego odkrywcy matematyka Benoita Mandelbrota.

Fraktal Mandelbrota jest określonym zbiorem punktów na płaszczyźnie liczb zespolonych. Kolor każdego punktu tego zbioru zależy z kolei od zachowania ciągu zdefiniowanego rekurencyjnie:
z_n+1 = z_n² + z₀                                                                                                   [1]
gdzie z – liczba zespolona.

Jeżeli liczbę z zapiszemy w postaci:
z = x + yi, gdzie:
x, y – współrzędne w układzie prostokątnym (kartezjańskim),
i – liczba urojona (i² = -1),
to po podstawieniu jej do wzoru [1] otrzymamy:
(x + yi)_n+1 = (x_n + y_ni)² + (x₀ + y₀i) = x_n² + 2x_ny_ni + (y_ni)² + x₀ + y₀i = x_n² + y_n²i² + 2x_ny_ni + x₀ + y₀i = x_n² – y_n² + 2x_ny_ni + x₀ + y₀i
Rozdzielając równania dotyczące części rzeczywistej i części urojonej,otrzymujemy:
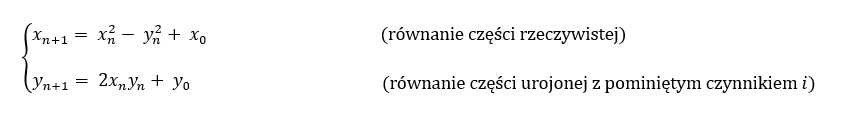{ x_n+1 = x_n² – y_n² + x₀  (równanie części rzeczywistej)
{                                                                                                                                                              [2]
{ y_n+1 = 2x_ny_n + y₀          (równanie części urojonej z pominiętym czynnikiem i)

Aby narysować fraktal Mandelbrota w zadanym obszarze prostokątnym, określonym przez (x_min, x_max) (y_min, y_max), gdzie (x_min, y_min) – współrzędne lewego dolnego wierzchołka obszaru, (x_max, y_max) – współrzędne prawego górnego wierzchołka obszaru,

postępujemy według następującego algorytmu:

1. Ustal współrzędne kolejnego punktu obszaru prostokątnego: (x₀, y₀).
2. Ustal numer iteracji n: n = 1.
3. Korzystając ze wzoru [2], oblicz (x_n, y_n).
4. Jeżeli odległość punktu (x_n, y_n) od punktu początku układu współrzędnych (0, 0) przekracza ustalony promień r, czyli: x_n²+ y_n²>r², to ciąg dąży do nieskończoności (dany punkt zachowuje się chaotycznie). Narysuj go kolorem ustalonym na podstawie aktualnego numeru iteracji n i przejdź do kroku 1.
5. W przeciwnym przypadku zwiększ numer iteracji: n = n + 1
6. Jeżeli numer iteracji przekroczył zadany próg p, to ciąg nie dąży do nieskończoności (punkt nie zachowuje się chaotycznie). Narysuj go kolorem czarnym i przejdź do kroku 1.
7. Idź do kroku 1.

Typowe parametry dla narysowania zbioru Mandelbrota to:
x_min = -2,5
x_max = 1,5
y_min = -1,25
y_max = 1,25
r = 2
p = 50

Ćwiczenie 8. Piszemy program rekurencyjnego tworzenia fraktala Mandelbrota

1. W pliku TC7_c8_Mandel.html zapisano program realizujący algorytm rekurencyjnego tworzenia fraktal Mandelbrota w języku JavaScript. Uruchom go w przeglądarce. Zobacz kod programu jako źródło strony (lub otwórz plik np. w Notatniku, w programie Notepad++).
2. Napisz w języku C++ funkcję Mandel(x, y, r, p), której parametrami są wartości (x₀, y₀) oraz liczby r i p. Funkcja powinna zwrócić 0, jeżeli punkt nie zachowuje się chaotycznie lub wartość n, jeżeli punkt zachowuje się chaotycznie.
   
   Wskazówki:

• Realizując algorytm za pomocą programu komputerowego, należy ustalić wielkość obrazu na ekranie komputera (w pikselach) i zamienić współrzędne ekranowe na współrzędne matematyczne.
• JavaScript ma składnię podobną do C++, więc, jeśli zmienimy słowo var na odpowiedni typ zmiennej – funkcja Mandel() w języku C++ będzie bardzo podobna. Czyli:

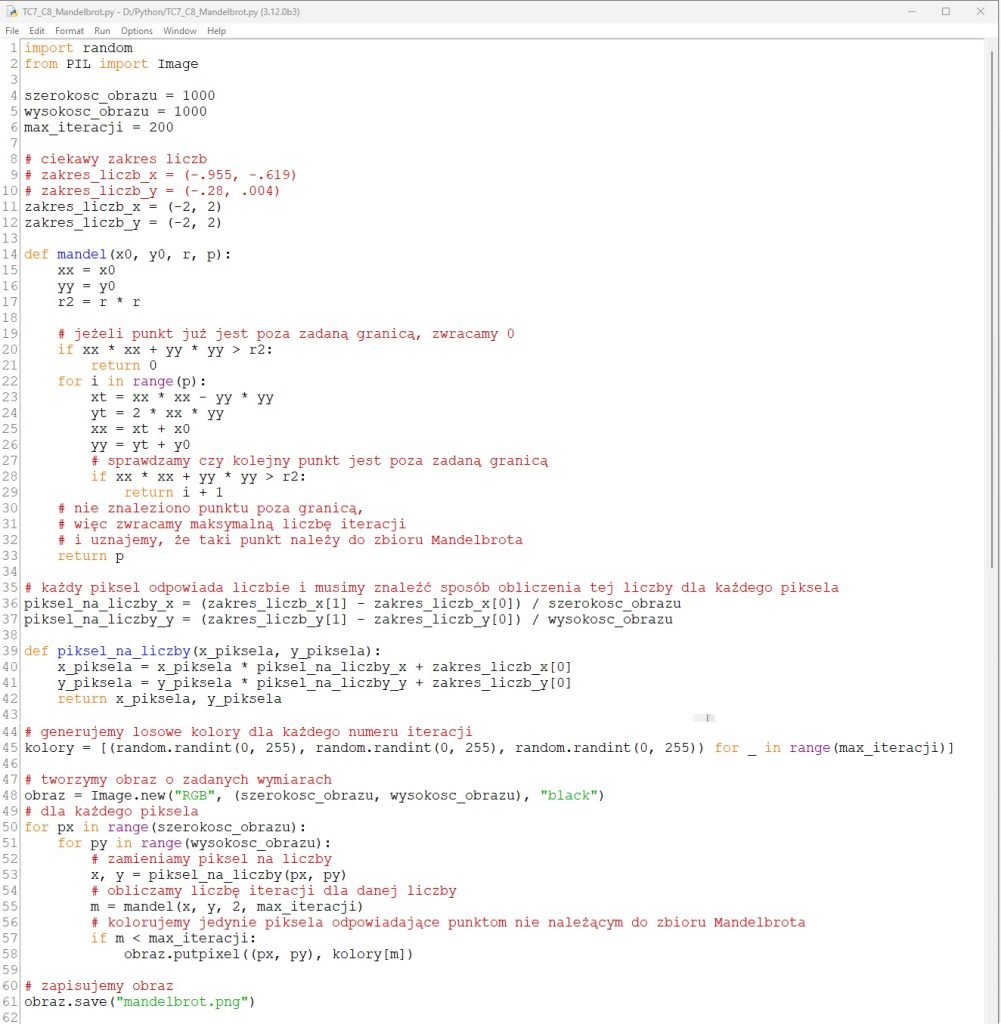
Przykład 3. Realizacja rekurencyjnego tworzenia fraktala Mandelbrota w języku Pyton

W języku Pyton możemy również napisać program realizujący algorytm rekurencyjnego tworzenia fraktal Mandelbrota. W tym celu wykorzystamy standardową bibliotekę Pillow, która pozwala bardzo prosto tworzyć i zapisywać obrazy.

Wynik działania programu (obraz – fraktal Mandelbrota zostanie zapisany w pliku z rozszerzeniem png (plik zostanie umieszczony w tym samym folderze co program).

Bibliotekę Pillow należy zwykle doinstalować. W tym celu w oknie Wiersz poleceniamożna wpisać polecenie:
pip install Pillow
Lub
pip3 install Pillow (jeśli używamy wersji Python 3, a pip domyślnie odnosi się do wersji Python. 
Po instalacji możesz zaimportować w programie bibliotekę: from PIL import Image – jak w poniższym programie.

Wskazówka: Aby uruchomić program systemu Windows Wiersz polecenia, można w polu Wyszukaj wpisać polecenie cmd inacisnąć Enter – otworzy się okno Wiersz polecenia.

Rys. 9.Fraktal Mandelbrota (obraz fraktala zapisany w pliku z rozszerzeniem png) – efekt wykonania programu w języku Python z przykładu 3.

Ćwiczenie 9. Analizujemy program rekurencyjnego tworzenia fraktala Mandelbrota w języku Python

1. Otwórz plik TC7_c9_Mandelbrot.py. Uruchom program.
2. Zapoznaj się z kodem programu. Przeanalizuj wstawione do kodu komentarze. Objaśnij działanie poszczególnych funkcji programu. Jakie struktury danych użyto w programie i dlaczego?

W pliku TC7_c9_Mandelbrot_turtle.py zapisano program tworzący fraktal Mandelbrota w języku Python, ale z wykorzystaniem grafiki żółwia. Niestety żółw nie nadaje się do rysowania Mandelbrota, ponieważ fraktal rysujemy w sposób rastrowy (piksel po pikselu), a żółw właściwie służy do tworzenia grafiki wektorowej. Dodatkowo program działa coraz wolniej po narysowaniu wielu kropek imitujących piksele.

Ćwiczenie 10. Porównujemy efekty wykonania programów tworzenia fraktala Mandelbrota w języku Python: programu wykorzystującego moduł turtle z programem wykorzystującym moduł pillow

1. Otwórz plik TC7_c10_Mandelbrot_turtle.py. Uruchom program.
2. Zapoznaj się z kodem programu. Przeanalizuj wstawione do kodu komentarze. Objaśnij działanie poszczególnych funkcji programu. Porównaj program i jego efekt z programem i jego efektem z ćwiczenia 8., w którym wykorzystano polecenia graficzne modułu pillow.

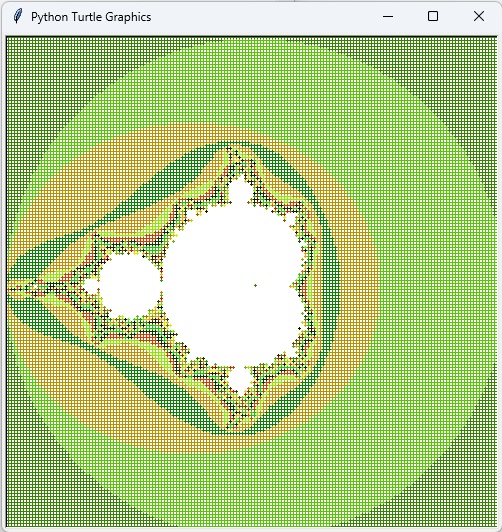
Rys. 10. Fraktal Mandelbrota – efekt wykonania programu w języku Python z wykorzystaniem grafiki żółwia (ćwiczenie 10.)

W Internecie znaleźć można wiele stron umożliwiających narysowanie fraktala Mandelbrota dla zadanych parametrów oraz powiększanie wybranych fragmentów.

Ćwiczenie 11. Oglądamy fraktale Mandelbrota

Znajdź jeden z dostępnych w Internecie generatorów fraktali Mandelbrota. Powiększ kilkanaście razy dowolny fragment brzegu (granicy pomiędzy obszarem czarnym a kolorowym) fraktala. Co zauważasz?

Zadania

1. Napisz w języku C++ program rekurencyjnego tworzenia fraktala Mandelbrota, który wyświetli fraktal za pomocą znaków gwiazdek „*”. Wykorzystaj schemat programu rysującego trójkąt Sierpińskiego zapisany w pliku TC7_c4_Sierpinski.cpp.
2. Znajdź w Internecie więcej informacji na temat L-systemów. Skorzystaj z generatora L-systemów programu Inkscape do narysowania obiektów przyrodniczych – różnego rodzaju drzew i krzewów.

3. Przypomnij sobie z tematu „Stosowanie wybranych funkcji w realizacji algorytmów i fraktali w arkuszu kalkulacyjnym” opis paprotki Barnsleya. Otwórz plik TB1_c11_p7_Barnsley.xls. Wylosuj kilkakrotnie nowe dane (klawisz F9) i zwróć uwagę na zmiany rysunku (wykresu) paprotki.

Dla zainteresowanych

4. Znajdź w Internecie informacje na temat zależności pomiędzy trójkątem Sierpińskiego a trójkątem Paskala.
5. Napisz w języku C++ program „rysujący” dywan Sierpińskiego w trybie tekstowym. Wykorzystaj schemat programu rysującego trójkąt Sierpińskiego zapisany w pliku TC7_c3_Sierpinski.cpp.
6. Odmianą fraktala Mandelbrota jest fraktal Julii, którego odkrywcą był francuski matematyk Gaston M. Julia (1893-1978). Znajdź w Internecie więcej informacji na temat fraktala Julii, w tym obrazów.