Temat B1. Stosowanie wybranych funkcji w realizacji algorytmów i fraktali w arkuszu kalkulacyjnym

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Uwaga: Zapoznaj się wcześniej z tematami B1 i B2 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa II”. Wykonaj zawarte w nich ćwiczenia i zadania.

Zapisy podstawy programowej realizowane w temacie:

II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.

Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

4) przygotowując opracowania rozwiązań złożonych problemów, posługuje się wybranymi aplikacjami w stopniu zaawansowanym:

c) stosuje zaawansowane funkcje arkusza kalkulacyjnego w zależności od rodzaju danych, definiuje makropolecenia, zna możliwości wbudowanego języka programowania,

Spis treści

1. Algorytmy liniowe w arkuszu kalkulacyjnym
2. Zastosowanie funkcji JEŻELI do realizacji algorytmów z warunkami
3. Realizowanie iteracji w arkuszu kalkulacyjnym
4. Zastosowanie algorytmów iteracyjnych w rysowaniu fraktali
   1. Śnieżynka Kocha
   2. Dywan i trójkąt Sierpińskiego
   3. „Gra w chaos”
   4. Paprotka Barnsleya

1. Algorytmy liniowe w arkuszu kalkulacyjnym

Większość obliczeń wykonywanych w szkole w arkuszu kalkulacyjnym przebiega według algorytmu liniowego. Poszczególne operacje następują krok po kroku w ustalonej z góry kolejności i nie ma potrzeby sprawdzania jakichkolwiek warunków. Algorytm liniowy jest podstawą obliczeń, takich jak sumowanie, potęgowanie, pierwiastkowanie, zaokrąglanie, obliczanie średniej, obliczanie wartości funkcji trygonometrycznych itp. Algorytm liniowy wykonujemy również wtedy, gdy powtarzamy daną instrukcję dla określonej liczby danych, zapisanych w kolumnach lub wierszach arkusza. W przypadku skomplikowanych zagadnień obliczeniowych algorytm liniowy może stanowić ich fragment.

Przykład 1. Zapisywanie algorytmu liniowego w arkuszu kalkulacyjnym

Zaprojektujemy w arkuszu kalkulacyjnym algorytm obliczający stan bankowej lokaty terminowej: dziesięciodniowej, oprocentowanej na 6,5% w stosunku rocznym, z kapitalizacją odsetek. Pokażemy, jak zmienia się stan kapitału i odsetek w okresie 150 dni, co 10 dni. Uogólnimy to zagadnienie, aby klient banku mógł sprawdzić, jak wzrosną jego oszczędności w zależności od kwoty początkowej i wysokości oprocentowania.

Oznaczenia:

l_r = 365 – liczba dni w roku,
k_p – kapitał początkowy,
k_k – kapitał końcowy,
p – oprocentowanie lokaty.

Wzór, według którego obliczymy wartość kapitału w danym okresie:

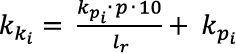
gdzie: i oznacza numer porządkowy okresu obliczeniowego.

Obliczane wartości przedstawimy w tabeli zawierającej kolumny określające oprocentowanie lokaty, numer porządkowy okresu obliczeniowego, kapitał początkowy w danym okresie obliczeniowym, odsetki oraz kapitał końcowy w danym okresie obliczeniowym (tzn. bieżącą wartość kapitału).

Po wpisaniu do komórki D2 wartości kapitału początkowego w pierwszym okresie obliczeniowym a do komórki E2 ‒ zerowych odsetek w pierwszym okresie formuła obliczająca wartość kapitału końcowego w komórce F2 ma postać: =D2+E2.

Kapitał początkowy w danym okresie równy jest kapitałowi końcowemu z poprzedniego okresu, natomiast formuła obliczająca odsetki w drugim okresie obliczeniowym ma postać: =D3*$A$2*10/365. Po skopiowaniu formuł do odpowiedniej liczby komórek otrzymamy wartości żądanych kwot.

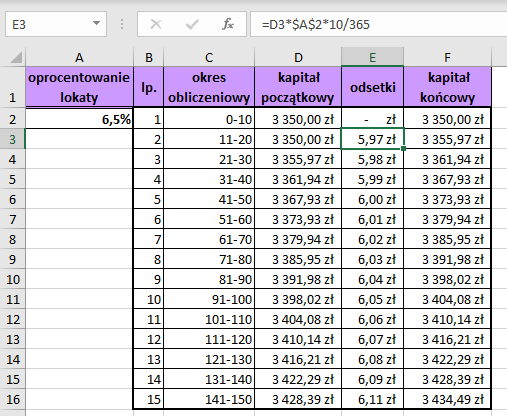
Rys. 1. Algorytm obliczania stanu bankowej lokaty terminowej opracowany w arkuszu kalkulacyjnym – przykład 1.

Ćwiczenie 1. Analizujemy realizację algorytmu liniowego w arkuszu kalkulacyjnym

1. Otwórz plik TB1_c1_p1.xls.
2. Przetestuj rozwiązanie zadania opisanego w przykładzie 1., zmieniając wysokość oprocentowania lokaty i kapitału początkowego. Wyjaśnij, dlaczego w formule umieszczonej w komórce E3 zastosowano adresowanie bezwzględne.

Ćwiczenie 2. Realizujemy algorytm liniowy w arkuszu kalkulacyjnym

1. Przedstaw w postaci listy kroków, a następnie w arkuszu kalkulacyjnym rozliczenie spłaty kredytu k_k, zaciągniętego na 36 miesięcy na 8% w stosunku rocznym.
   Spłata powinna być podzielona na comiesięczne raty. Każda rata będzie naliczana według wzoru:
   ,
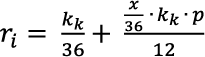   gdzie:
   x – liczba miesięcy do końca spłacania kredytu,
   p – wartość oprocentowania kredytu,
   k_k – kwota kredytu,
   r_i – wartość raty w i-tym okresie.
2. Zapisz plik pod nazwą TB1_c2.
   Wskazówka: Przyjmij, że kwota kredytu co miesiąc pomniejszy się o spłaconą ratę i dopiero od tak pomniejszonej kwoty będą naliczane odsetki.

2. Zastosowanie funkcji JEŻELI do realizacji algorytmów z warunkami

W arkuszu kalkulacyjnym algorytmy z warunkami wykorzystuje się do tworzenia zestawień statystycznych oraz przeprowadzania skomplikowanych obliczeń matematycznych, fizycznych, chemicznych itp.

Przykład 2. Zapisywanie prostej sytuacji warunkowej w arkuszu kalkulacyjnym

Zapiszemy w arkuszu kalkulacyjnym algorytm obliczania płacy za nadgodziny, zawierający prostą sytuację warunkową, uzależniającą wysokość premii za nadgodziny od ich liczby. Wykorzystamy funkcję logiczną JEŻELI. Należy wyznaczyć komórki, do których będziemy wpisywać stawkę podstawową za jedną nadgodzinę, liczbę przepracowanych nadgodzin, liczbę nadgodzin bez dodatku (norma) oraz wielkość dodatku (w procentach) za nadgodziny powyżej normy. Następnie do komórki, w której ma być obliczana płaca, należy wpisać formułę zawierającą funkcję warunkową JEŻELI.

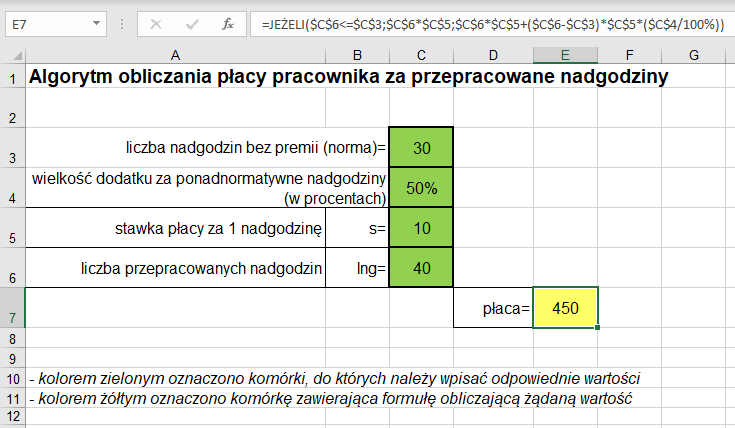
Ćwiczenie 3. Analizujemy realizację algorytmu z warunkami w arkuszu kalkulacyjnym

1. Otwórz plik TB1_c3_p2.xls.
2. Przeanalizuj postać formuły umieszczonej w komórce E7. Przetestuj rozwiązanie zadania opisanego w przykładzie 2. dla wybranych danych.

Ćwiczenie 4. Realizujemy algorytm z warunkami w arkuszu kalkulacyjnym

1. Wykonaj w arkuszu kalkulacyjnym zadanie: Jeśli klasa otrzyma od 100 do 150 punktów we współzawodnictwie (150 jest maksymalną liczbą punktów), otrzymuje nagrodę z puli funduszu rady rodziców w postaci dopłaty do wycieczki w wysokości 1/3 kosztów i dodatek w wysokości 20% kosztów. Jeśli zdobędzie poniżej 100 punktów, otrzymuje tylko procentowy dodatek. Oblicz kwotę dofinansowania.
2. Zapisz plik pod nazwą TB1_c4.
3. Sprawdź rozwiązanie dla następujących par danych (punkty; koszty): (120; 4250), (30; 2800), (100; 3500), (0; 3000), (78; 4380).

Przykład 3. Zapisywanie warunków zagnieżdżonych w arkuszu kalkulacyjnym

Rozwiązanie równania kwadratowego wymaga sprawdzenia dwóch warunków, przy czym drugi warunek jest umieszczony (zagnieżdżony) w pierwszym:

1. Czy Δ < 0? (jeśli tak, to równanie nie ma rozwiązania w zbiorze liczb rzeczywistych;
   w przeciwnym przypadku rozpatrujemy kolejny warunek).
2. Czy Δ = 0? (jeśli tak, to równanie ma jeden pierwiastek rzeczywisty (podwójny);
   w przeciwnym wypadku równanie ma dwa różne pierwiastki rzeczywiste).

Drugi warunek jest rozpatrywany w przypadku niespełnienia pierwszego. Aby zapisać taką sytuację w arkuszu kalkulacyjnym, należy użyć zagnieżdżonych funkcji JEŻELI.

Powtórzenie wiadomości z matematyki:
Równanie kwadratowe
ax² + bx + c = 0, gdzie a ≠ 0, w zależności od znaku wyróżnika Δ (delty) ma trzy możliwe rozwiązania:
– dla Δ < 0 brak pierwiastków rzeczywistych,
– dla Δ = 0 jeden pierwiastek rzeczywisty (podwójny),
– dla Δ > 0 dwa różne pierwiastki rzeczywiste.

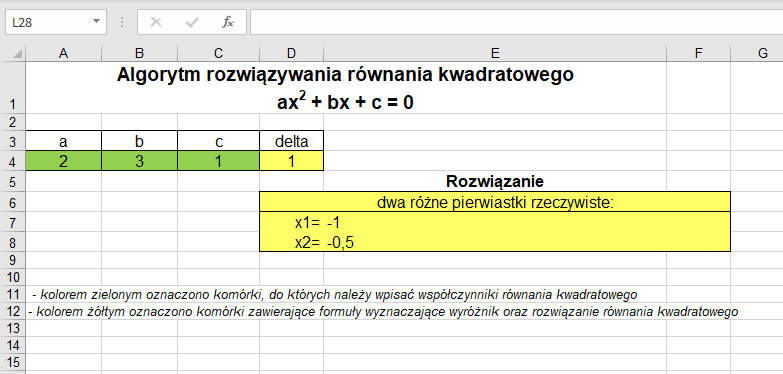
W przykładzie 3. uwzględniono przypadki, gdy równanie nie posiada rozwiązania w zbiorze liczb rzeczywistych (Δ < 0), gdy rozwiązaniem jest jeden pierwiastek podwójny (Δ = 0) lub dwa różne pierwiastki rzeczywiste (Δ > 0). Umieszczenie w jednym warunku kolejnego warunku (zagnieżdżenie warunków) pozwala na rozpatrzenie większej liczby alternatywnych rozwiązań.

Warto pamiętać, że gdy wyniki obliczeń są liczbami niewymiernymi, zostaną wyświetlone ich rozwinięcia dziesiętne. Ze względu na ograniczenia poszczególnych formatów liczbowych, będą one miały wartości przybliżone.

Ćwiczenie 5. Analizujemy realizację algorytmu z warunkami zagnieżdżonymi w arkuszu kalkulacyjnym

1. Otwórz plik TB1_c5_p3.xls.
2. Zapoznaj się z formułami wyliczającymi pierwiastki równania kwadratowego. Przetestuj rozwiązanie zadania opisanego w przykładzie 3. dla wybranych danych.

Ćwiczenie 6. Realizujemy algorytm rozwiązywania równania liniowego w arkuszu kalkulacyjnym

1. W pliku TB1_c6.doc zapisano listę kroków rozwiązywania równania liniowego. Na jej podstawie opracuj w arkuszu kalkulacyjnym algorytm rozwiązywania równania liniowego.
2. Zapisz plik pod nazwą TB1_c6.

3. Realizowanie iteracji w arkuszu kalkulacyjnym

W arkuszu kalkulacyjnym iterację realizuje się za pomocą kopiowania formuł. Formułę można skopiować tyle razy, ile kroków wymaga dane zadanie obliczeniowe.

Przykład 4. Sprawdzanie, czy dana liczba jest liczbą pierwszą

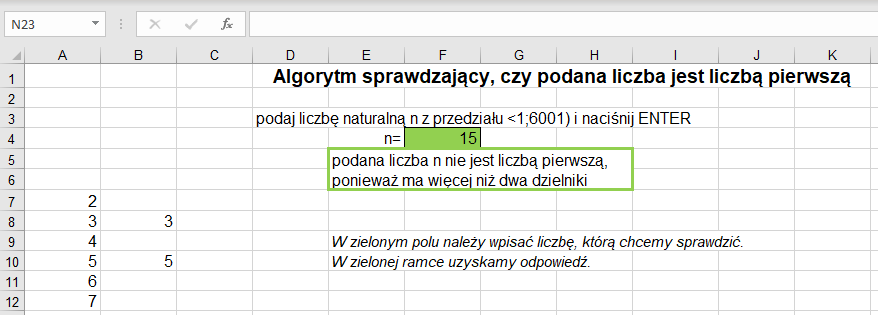
Sprawdzimy, czy liczba naturalna n z zadanego przedziału liczbowego (1;6001) jest liczbą pierwszą.

Do rozwiązania zadania zastosujemy algorytm sprawdzający, czy dana liczba jest podzielna przez liczby naturalne mniejsze od niej i obliczający ilość dzielników.

Realizując ten algorytm w arkuszu kalkulacyjnym, można wykorzystać funkcję MOD(liczba;dzielnik), zwracającą resztę z dzielenia liczby przez dzielnik. W pierwszej kolumnie umieszczamy kolejne liczby z zadanego przedziału (będą to dzielniki), a w sąsiedniej kolumnie – formułę sprawdzającą, czy wybrana liczba n jest podzielna przez liczbę z poprzedniej kolumny i zwracającą wartość dzielnika lub pustą komórkę. Następnie wystarczy zliczyć, ile jest dzielników w drugiej kolumnie, i na tej podstawie określić, czy wybrana liczba jest liczbą pierwszą.

Formuła w komórce E5 ma postać:
=JEŻELI($F$4<=1;”liczba nie należy do zadanego przedziału”;JEŻELI($F$4>=6001;”liczba nie należy do zadanego przedziału”;JEŻELI(ILE.LICZB($B$7:$B$6005)=1;”podana liczba n jest liczbą pierwszą”;”podana liczba n nie jest liczbą pierwszą, ponieważ ma więcej niż dwa dzielniki”))).

Powtórzenie wiadomości z matematyki:
Liczba pierwsza to liczba naturalna większa od jeden, podzielna tylko przez liczbę jeden i samą siebie, np. 2 = 1•2; 3 = 1•3; 5 = 1•5 itd.
Pojęcie liczb pierwszych wprowadził Euklides.
Rozkład na czynniki pierwsze to przedstawienie liczby w postaci iloczynu liczb pierwszych. Jedno z zasadniczych twierdzeń arytmetyki mówi, że takie przedstawienie jest jednoznaczne.

Algorytm jest uproszczony ze względu na ograniczony i z góry określony przedział, z jakiego będą pochodzić rozpatrywane liczby. Zakres wartości badanych liczb można oczywiście poszerzyć, ustalając na początku granice przedziału.

Ćwiczenie 7. Analizujemy realizację algorytmu iteracyjnego w arkuszu kalkulacyjnym

1. Otwórz plik TB1_c7_p4.xls.
2. Przetestuj rozwiązanie zadania opisanego w przykładzie 4. dla wybranych danych.

4. Zastosowanie algorytmów iteracyjnych w rysowaniu fraktali

Algorytmy iteracyjne wykorzystuje się w geometrii fraktalnej. Fraktale istnieją w świecie idealnych konstrukcji matematycznych, ale powstały w wyniku inspiracji naukami przyrodniczymi.
W naturze istnieje wiele tworów, które swym kształtem przypominają fraktale (np. płatek śniegu, liść paproci, brokuł, kalafior, kalafior romanesco).

Fraktalem nazywamy figurę geometryczną mającą cechę samopodobieństwa, tzn. taką, której dowolny fragment po powiększeniu jest taki sam jak całość figury (każda część wygląda jak pomniejszona całość).

Dzięki komputerom powstała możliwość efektywnego badania fraktali. Mają one zastosowanie w wielu dziedzinach, takich jak: fizyka, biologia, geologia, technika, nauki społeczne, medycyna. Za pomocą geometrii fraktalnej można opisywać zjawiska i obiekty, które do tej pory nie dawały się formalnie opisać (np. płuca, układ krwionośny, chmury lub liście).

Geometria fraktalna jest często nazywana geometrią chaosu. Stanowi ona nowy język, który może być używany do opisu złożonych zjawisk i form występujących w naturze. Elementów tego języka nie można bezpośrednio zaobserwować. Są nimi algorytmy, w wyniku których powstają kształty i struktury możliwe do uzyskania jedynie za pomocą komputera. W grafice komputerowej fraktale znajdują zastosowanie w kodowaniu obrazów.

4.1. Śnieżynka Kocha

Pojęcie fraktali zostało wprowadzone do matematyki w 1975 roku przez francuskiego matematyka Benoit Mandelbrota, który urodził się w 1924 roku w Warszawie. Jednak już w roku 1904 znany był fraktal zwany śnieżynką Kocha. Powstaje on w ten sposób, że do boków trójkąta równobocznego „dokleja się” trzy trójkąty pomniejszone, np. w skali 1:3; do otrzymanej gwiazdy sześcioramiennej – 12 trójkątów zmniejszonych, np. w skali 1:9 itd. Figura otrzymana po wykonaniu nieskończenie wiele razy tej konstrukcji ma brzeg nieskończonej długości, chociaż otacza on skończone pole. Śnieżynka Kocha jest jednym z najprostszych modeli matematycznych pełnej linii brzegowej, np. oddzielającej morze od lądu.

4.2. Dywan i trójkąt Sierpińskiego

Wybitny polski matematyk, profesor Wacław Sierpiński (1882-1969), opracował dwa fraktale: tzw. dywan Sierpińskiego i trójkąt Sierpińskiego. Dywan Sierpińskiego powstaje w nieskończonym procesie kolejnych podziałów kwadratu na dziewięć kwadratów przystających, z których usuwamy środkowy.

Podstawowy krok algorytmu konstruowania trójkąta Sierpińskiego polega na znalezieniu w trójkącie o dowolnej długości boków ich środków. Po połączeniu punkty te wraz z wierzchołkami trójkąta wyznaczają cztery mniejsze trójkąty, z których usuwamy środkowy. W pierwszym kroku konstrukcji otrzymujemy trzy przystające trójkąty, których boki są równe połowom odpowiednich boków trójkąta początkowego. Następnie powtarzamy procedurę dla każdego z pozostałych trzech trójkątów itd. W kolejnych krokach otrzymamy 3, 9, 27, 81… (ogólnie 3n) trójkątów, z których każdy jest pomniejszoną kopią figury z poprzedniego kroku.

Czy wiesz, że:
trójkąt Sierpińskiego nazywany jest także „uszczelką Sierpińskiego”?

Ćwiczenie 8. Szkicujemy trójkąt Sierpińskiego

Naszkicuj na kartce obraz, który otrzymamy po wykonaniu trzech kroków algorytmu konstruowania trójkąta Sierpińskiego.

4.3. „Gra w chaos”

Trójkąt Sierpińskiego można również otrzymać w sposób, wydawałoby się, zupełnie nieoczekiwany – jako wynik losowego eksperymentu „gry w chaos”. Zanim przedstawimy ten algorytm w arkuszu kalkulacyjnym, wyjaśnimy zasady „gry w chaos”.

Przykład 5. Przedstawienie zasad „gry w chaos”

Wybieramy trzy punkty na płaszczyźnie i oznaczamy je numerami 1, 2, 3.

Są to tzw. punkty bazowe. Następnie wybieramy jeszcze jeden dowolny punkt, tzw. punkt wiodący.

Krok 1.
Losujemy jedną z trzech liczb będących numerami punktów bazowych.
Jeśli otrzymamy np. liczbę 3, wyznaczamy odcinek pomiędzy punktem wiodącym a punktem bazowym o numerze 3 i znajdujemy jego środek. Punkt ten będzie teraz nowym punktem wiodącym.

Krok 2.
Ponownie losujemy jedną z trzech liczb: 1, 2 lub 3 i, postępując jak w poprzednim kroku, wyznaczamy kolejny punkt wiodący itd.
Zaczynając od dowolnego punktu i postępując według wyżej opisanej procedury, musimy w którymś z kolejnych kroków trafić do wnętrza trójkąta utworzonego przez punkty bazowe. Ponadto nietrudno spostrzec, że jeśli punkt wiodący raz dostanie się do wnętrza tego trójkąta, to zostanie tam na zawsze. Ponieważ punkty wiodące generujemy losowo, wydawałoby się, że otrzymany w ten sposób układ punktów będzie chaotyczny. Jednak po wykonaniu kilku tysięcy takich kroków zauważymy, że powstała konstrukcja ma niezwykle uporządkowany charakter. Jest to trójkąt Sierpińskiego.

Ćwiczenie 9.
Przeprowadź w zeszycie kilka pierwszych kroków „gry w chaos”. Przyjrzyj się efektom.

Przykład 6. Przedstawienie algorytmu „gry w chaos” w arkuszu kalkulacyjnym

W pliku Sierpiński.xls algorytm „gry w chaos” przedstawiono w arkuszu kalkulacyjnym.
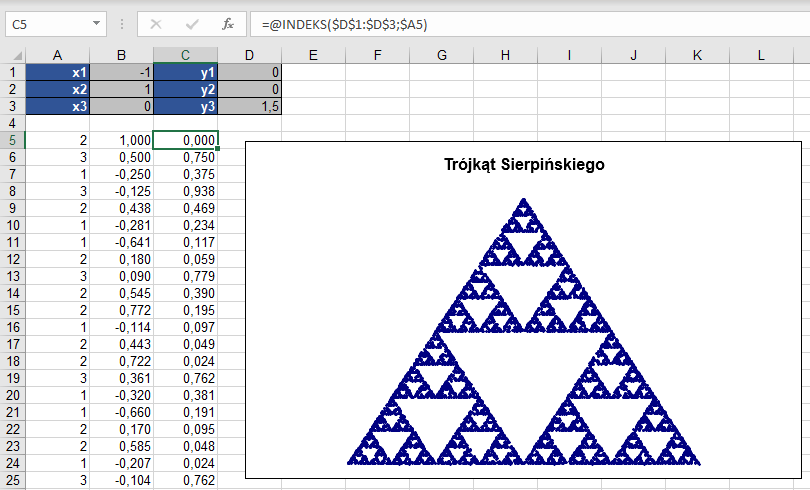
Jako trzy punkty bazowe wybrano punkty o współrzędnych (-1; 0), (1; 0), (0; 1,5). Za każdym razem do wylosowania jednego z nich użyto generatora liczb losowych: funkcji LOS().
Do wyznaczania współrzędnych kolejnych punktów wiodących zastosowano funkcję INDEKS.
W algorytmie tym wykonuje się 9994 kroków iteracyjnych. Pozwala to na otrzymanie na wykresie obrazu trójkąta Sierpińskiego.

Ćwiczenie 10. Analizujemy realizację „gry w chaos”

1. Otwórz plik TB1_c10_p6_Sierpiński.xls.
2. Zapoznaj się ze sposobem wykonania algorytmu „gry w chaos”. Przeanalizuj zastosowane w nim formuły.
   Wskazówka: Naciskając klawisz F9, wylosujesz nowy zestaw liczb.

4.4. Paprotka Barnsleya

Fraktal zwany paprotką Barnsleya, o kształcie przypominającym liść paproci, odkrył Michael F. Barnsley. Fraktal ten można opisać za pomocą przekształceń afinicznych.

Przekształcenie afiniczne to wzajemnie jednoznaczne przekształcenie geometryczne, w którym obrazem prostej jest inna prosta. Przekształceniami afinicznymi na płaszczyźnie są np.: symetria osiowa, symetria środkowa, przesunięcie równoległe, obrót, jednokładność, powinowactwo prostokątne i każde złożenie tych przekształceń. Przekształcenie afiniczne na płaszczyźnie opisują następujące zależności:

    x’ = ax + by + e             [1]
    y’ = cx + dy + f              [2]

gdzie:

a, b, c, d, e, f – współczynniki przekształcenia (gdzie a • b ≠ b • c),
x, y – współrzędne punktu przed przekształceniem,
x’, y’ – współrzędne punktu po przekształceniu.

W przypadku trójkąta Sierpińskiego „gra w chaos” sprowadzała się do przekształcenia współrzędnych punktu wiodącego za pomocą jednego z trzech przekształceń afinicznych opisanych współczynnikami podanymi w tabeli 1.

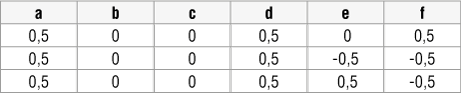
W tym przypadku prawdopodobieństwo wylosowania danego przekształcenia jest zawsze takie samo i wynosi 1/3.

W przypadku paprotki Barnsleya przekształcenia opisano za pomocą współczynników podanych w tabeli 2. (w ostatniej kolumnie podano prawdopodobieństwo wylosowania danego

przekształcenia).

Przykład 7. Rysowanie paprotki Barnsleya w arkuszu kalkulacyjnym

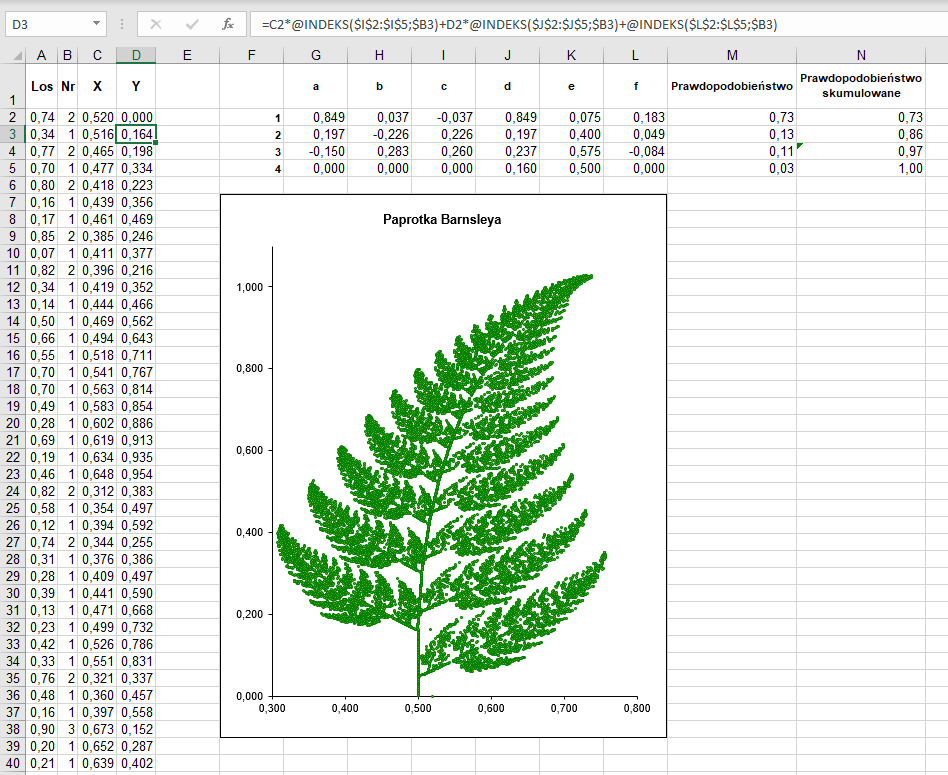
Aby narysować paprotkę Barnsleya w arkuszu kalkulacyjnym, wyznaczamy odpowiednio dużą (w naszym przypadku – 20000) liczbę współrzędnych punktu wiodącego, poddanego przekształceniom afinicznym, opisanym współczynnikami ujętymi w tabeli 2.

Dla każdego punktu losujemy przy użyciu funkcji LOS() liczbę, która posłuży do wyboru jednego z przekształceń (kolumna A arkusza).

Następnie przy użyciu funkcji JEŻELI() sprawdzamy, w którym z przedziałów prawdopodobieństw mieści się wylosowana liczba, wybierając w ten sposób numer przekształcenia (kolumna B).

Korzystając ze wzorów [1] i [2], w kolumnach C i D obliczamy nowe współrzędne punktu wiodącego (w wierszu 2. ręcznie wpisujemy jego początkowe współrzędne).

Wszystkie obliczone współrzędne punktów przedstawiamy na wykresie typu XY (punktowy), wybierając, odpowiedni dla paprotki, zielony kolor.

Ćwiczenie 11. Analizujemy algorytm konstruowania paprotki Barnsleya

Zapoznaj się z algorytmem konstruowania paprotki Barnsleya, zapisanym w pliku TB1_c11_p7_Barnsley.xls. Wylosuj kilkakrotnie nowe dane (klawisz F9) i zwróć uwagę na zmiany rysunku (wykresu) paprotki.

Zadania

1. Wykonaj w arkuszu kalkulacyjnym algorytm obliczania pola kwadratu o boku a, gdzie a jest dowolną liczbą całkowitą. Dla liczb niedodatnich powinien być wyprowadzany napis błędna liczba.
2. Wykonaj w arkuszu kalkulacyjnym algorytm sprawdzania warunku istnienia trójkąta.
3. Wyjaśnij sposób tworzenia śnieżynki Kocha. Jakie czynności wykonuje się w jednym kroku iteracji? Narysuj śnieżynkę w zeszycie.

Dla zainteresowanych

4. Przygotuj w arkuszu kalkulacyjnym algorytm rozwiązywania układu dwóch równań liniowych metodą wyznaczników.
5. Korzystając z Internetu i innych źródeł, znajdź dodatkowe informacje na temat geometrii fraktalnej, m.in. dotyczące jej zastosowań.