Zastosowanie rekurencji do generowania ciągów liczb

Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. wyróżnia w problemie podproblemy i charakteryzuje: metodę połowienia, podejście zachłanne i rekurencję,
4. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

3. objaśnia oraz porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przykłady problemów i algorytmów, w szczególności:
   b) rekurencję (do generowania ciągów liczb, potęgowania, sortowania liczb, generowania fraktali),

Spis treści

1. Rekurencja
2. Rekurencyjne generowanie ciągu n – liczb naturalnych nieparzystych
3. Rekurencyjne obliczanie wartości elementów ciągu Fibonacciego
4. Rekurencyjne generowanie ciągu liczb pierwszych
5. Ciągi matematyczne określone wzorem rekurencyjnym

1. Rekurencja

Podczas rozwiązywania problemu możemy skorzystać z rozwiązania, które wypracowaliśmy wcześniej przy podobnym problemie. Możemy też podzielić problem na mniejsze podproblemy, które będzie nam łatwiej rozwiązać, a później przejść do rozwiązania całego problemu.

Możemy również w problemie i jego algorytmie (sposobie rozwiązania) wyodrębnić części podobne do całości i zmienić algorytm tak, aby korzystał z siebie samego.

Rys. 1. Wizualny efekt zjawiska rekurencji

Z rekurencją mamy do czynienia, gdy, określając jakieś pojęcie, odwołujemy się w definicji do niego samego.

Rekurencję stosujemy często w definicjach matematycznych. Zjawiska rekurencyjne występują również w naszym otoczeniu. Na rysunku 1. rekurencja jest przedstawiona w postaci „zagłębiających się w siebie”, podobnych, coraz to mniejszych fi gur geometrycznych.

Podobny efekt możemy uzyskać dzięki odbiciom w lustrze. Wystarczy, patrząc w jedno lustro, nakierować na nie drugie, najlepiej mniejsze, owalne. Uzyskamy wówczas ciąg odbić mieszczących się jedno w drugim.

Ćwiczenie 1. Podajemy przykłady zjawisk rekurencyjnych

Podaj przykłady zjawisk rekurencyjnych, które można spotkać w życiu codziennym lub które znasz z przedmiotów szkolnych.

Rekurencja i iteracja różnią się zasadniczo. Powtórzenia w rekurencji są innego rodzaju niż powtórzenia właściwe dla iteracji. Powtórzenia w rekurencji „zagłębiają się w siebie” na zasadzie powrotu do tej samej definicji.

2. Rekurencyjne generowanie ciągu n liczb naturalnych nieparzystych

W definicji zbioru liczb naturalnych następuje odwołanie do tej definicji, czyli jest do definicja rekurencyjna.

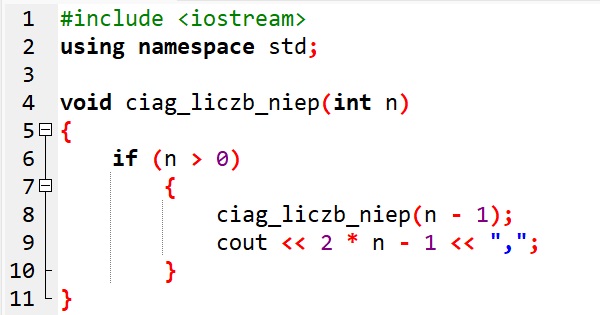
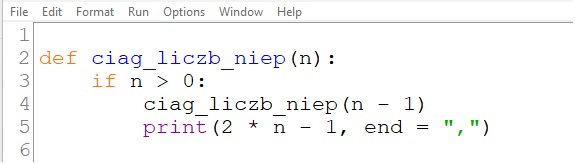
W przykładzie 1. pokazano kody rekurencyjnej funkcji generującej n liczb naturalnych nieparzystych ciag_liczb_niep(n) w językach C++ i Python. W wierszu 8. (C++) i w wierszu 4. (Python) widzimy wywołanie rekurencyjne tej samej funkcji, ale z parametrem n – 1.

Przykład 1. Rekurencyjna definicja funkcji generującej n liczb naturalnych nieparzystych

Ćwiczenie 2. Piszemy program generujący ciąg liczb naturalnych nieparzystych w wersji rekurencyjnej

1. Otwórz plik TC6_p1_c2_ciag_liczb_niep.cpp lub TC6_p1_c2_ciag_liczb_niep.py.
2. Napisz program generujący metodą rekurencyjną ciąg n liczb naturalnych nieparzystych. W programie wykorzystaj funkcję ciag_liczb_niep() z przykładu 1.
3. Zapisz program w pliku pod tą samą nazwą.

3. Rekurencyjne obliczanie wartości elementów ciągu Fibonacciego

W roku 1202 wybitny włoski matematyk okresu średniowiecza, Leonardo Pisano, zwany Fibonaccim, przedstawił problem, który do tej pory dostarcza natchnienia rzeszom matematyków. Dotyczy on liczebności populacji królików.

Opis problemu

Początkowo rodzi się para królików, która po miesiącu osiąga dojrzałość. Po następnym miesiącu wydaje na świat parę królików, po miesiącu następną parę i tak dalej, tzn. pierwsza para co miesiąc wydaje na świat potomstwo (parę królików). Z kolei każda nowa para po miesiącu osiąga dojrzałość i po każdym następnym miesiącu również wydaje na świat kolejną parę królików. Proces ten nie ma końca. Zakładamy, że króliki żyją wiecznie. Pytanie brzmi: jaka jest liczba par królików po n miesiącach?

Opis algorytmu

Zauważmy, że liczba par królików w danym miesiącu (z wyjątkiem pierwszego i drugiego miesiąca) zależy od dwóch wartości: liczby par królików dorosłych i liczby par królików młodych w poprzednim miesiącu. Tych ostatnich jest z kolei tyle, ile było par królików dorosłych dwa miesiące wcześniej.

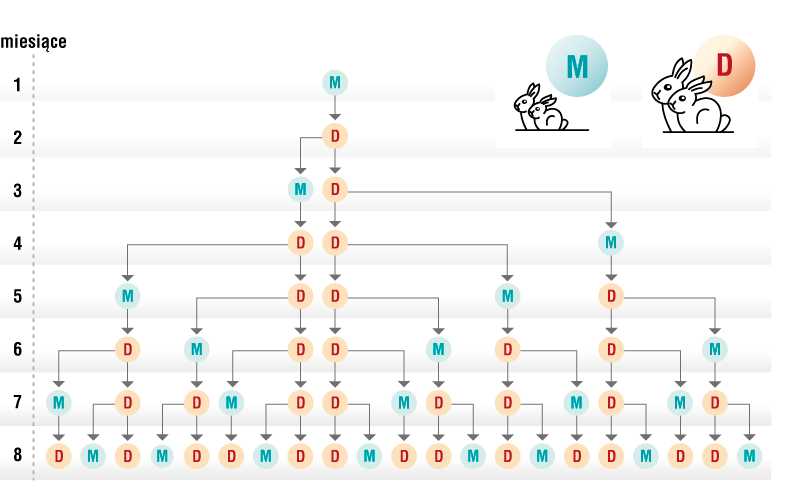
Rys. 2. Schemat przedstawia liczebność populacji królików w pierwszych ośmiu miesiącach doświadczenia (M – para królików młodych, D – para królików dojrzałych); ósma liczba Fibonacciego to 21 par

Jeśli oznaczymy całkowitą liczbę par królików w n-tym miesiącu jako Fn, to będziemy ją mogli określić następująco:

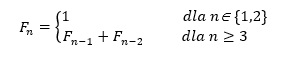
Liczba Fn opisuje całkowitą wielkość populacji królików po upływie n miesięcy i nazywana jest liczbą Fibonacciego. Natomiast ciąg liczb naturalnych, w którym każda liczba (z wyjątkiem pierwszej i drugiej) jest sumą dwóch poprzednich, nazywamy ciągiem Fibonacciego.

Podana definicja ciągu Fibonacciego jest rekurencyjna, gdyż odwołuje się do siebie samej. Oto kilka początkowych liczb tego ciągu:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Obliczenia czwartej liczby Fibonacciego wynikające z definicji rekurencyjnej, czyli dla n = 4:

F4 = F3 + F2 = (F2 + F1) + 1 = (1 + 1) + 1 = 2 + 1 = 3.

Na rysunku 4. pokazano schemat rekurencyjnych obliczeń czwartej liczby Fibonacciego (F4):

• aby obliczyć F4, musimy znać wartość F3 i F2;
• aby obliczyć F3, musimy znać wartość F2 i F1.

W ten sposób powstaje tzw. stos, na którym dostępny jest tylko element znajdujący się na wierzchołku, czyli wartość pierwszej liczby Fibonacciego = 1. „Zdejmując” z góry wartości liczb Fibonacciego ze stosu, dojdziemy do wartości czwartej liczby, czyli 3.

Ćwiczenie 3. Obliczamy wybrane liczby Fibonacciego

Oblicz trzecią i szóstą liczbę ciągu Fibonacciego. Czy możesz obliczyć szóstą liczbę bez wcześniejszego obliczenia czwartej i piątej? Uzasadnij odpowiedź.

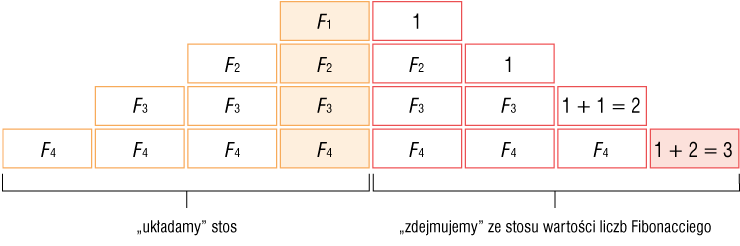
Rys. 3. Schemat rekurencyjnego obliczenia czwartej liczby Fibonacciego

Definicja ciągu Fibonacciego jest rekurencyjna, gdyż odwołuje się do samej siebie.

Aby obliczyć poszczególne liczby Fibonacciego, można posłużyć się zarówno algorytmem iteracyjnym, jak i rekurencyjnym. Jednak w tym przypadku algorytm w postaci rekurencyjnej wymaga wykonania dużo większej liczby kroków obliczeniowych niż ten sam algorytm w postaci iteracyjnej.

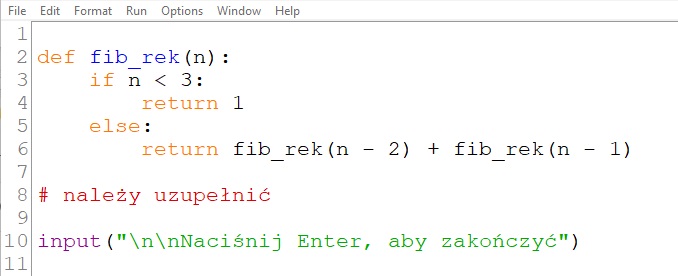
Przykład 2. Rekurencyjna definicja funkcji obliczającej liczby Fibonacciego w językach C++ i Python

Ćwiczenie 4. Zapisujemy w postaci programu rekurencyjną realizację algorytmu obliczającego liczby Fibonacciego

1. Napisz specyfikację zadania i listę kroków obliczania liczb Fibonacciego.
2. Otwórz pliki TC6_p2_c4_Fibonacci_rekurencyjnie.cpp lub TC6_p2_c4_Fibonacci_rekurencyjnie.py. Korzystając z wybranej definicji funkcji, napisz program w wersji rekurencyjnej, obliczający k-tą liczbę Fibonacciego. Omów działanie funkcji – wyjaśnij zapis:
fib_rek(n - 2) + fib_rek(n - 1).
3. Funkcję fib_rek() wywołaj w programie głównym z parametrem aktualnym k.
4. Zapisz program w pliku pod tą samą nazwą i przetestuj dla różnych danych.

4. Rekurencyjne generowanie ciągu liczb pierwszych

Ćwiczenie 5.

Przypomnij sobie z wybranego podręcznika do zakresu podstawowego treści dotyczące liczb pierwszych i tworzenia programu realizujące algorytm badania pierwszości liczby: z tematu C4 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa II” lub z tematów 86 i 97 z podręcznika „Informatyka 1-3. Podręcznik dla szkoły ponadpodstawowej. Zakres podstawowy”.

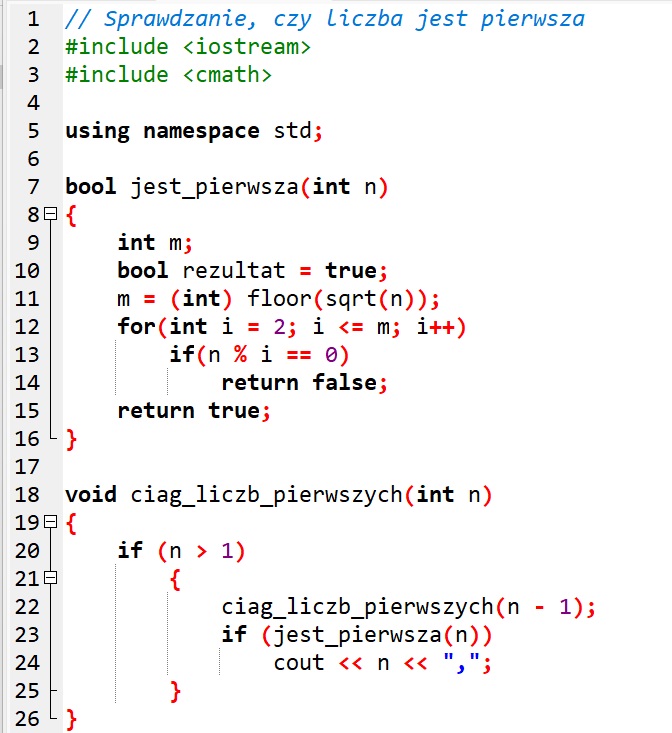
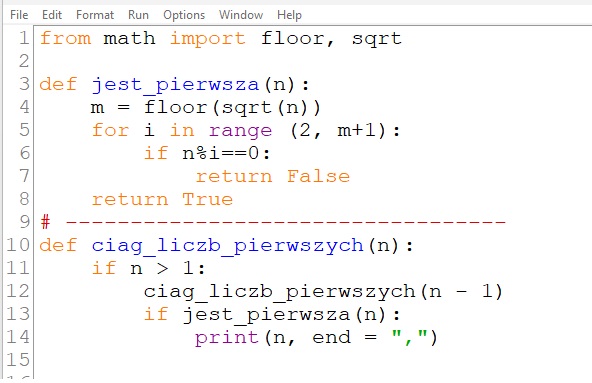
Przykład 3. Rekurencyjna definicja funkcji generującej ciąg liczb pierwszych w językach C++ i Python

Ćwiczenie 6. Piszemy program generujący ciąg liczb pierwszych do danego zakresu w wersji rekurencyjnej

1. Otwórz pliki TC6_p3_c6_ liczby_pierwsze.cpp lub TC6_p3_c6_liczby_pierwsze.py.
2. Napisz program generujący metodą rekurencyjną ciąg liczb pierwszych nie większych niż wartość zmiennej zakres (wartość zmiennej zakres podawana ma być z klawiatury po uruchomieniu programu). W programie wykorzystaj zdefiniowane funkcje: czy_pierwsza(n) oraz ciag_liczb_pierwszych(n). Objaśnij działanie tych funkcji.
3. Zapisz program w pliku pod tą samą nazwą.

5. Ciągi matematyczne określone wzorem rekurencyjnym

Jednym z ciekawych ciągów w matematyce jest ciąg następujących liczb: 1, 3, 6, 10, 15, 20, …. Pierwszym wyrazem tego ciągu jest 1. Każdy następny element tego ciągu jest sumą wartości elementu poprzedniego i numeru tego elementu. Np. wartość trzeciego elementu ciągu (6) otrzymujemy jako sumę wartość elementu poprzedniego (3) oraz numeru tego elementu (3). Wartość czwartego (10) jako sumę wartości elementu poprzedniego (6) oraz numeru elementu (4). Liczby w tym ciągu nazywane są liczbami trójkątnymi, ponieważ można je sobie wyobrazić jako układ trójkątnych obiektów (rys. 4.).

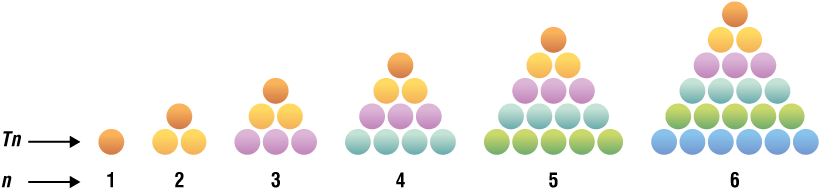
Rys. 4. Ilustracja graficzna sześciu pierwszych liczb trójkątnych

Wzór na n-tą liczbę trójkątną ma postać:

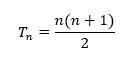
Możemy go również przedstawić rekurencyjnie, wykorzystując definicję tego ciągu.

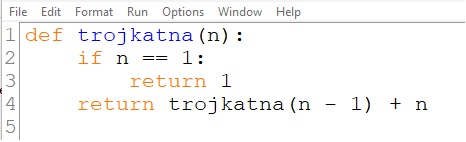
Przykład 4. Rekurencyjna funkcja wyznaczająca wartość n-tego elementu ciągu liczb trójkątnych w językach C++ i Python

Ćwiczenie 7. Piszemy program generujący ciąg liczb trójkątnych w wersji rekurencyjnej

1. Otwórz pliki TC6_p4_c7_liczby_trojkatne.cpp lub TC6_p4_c7_liczby_trojkatne.py.
2. Napisz program generujący metodą rekurencyjną wartość n-tej liczby trójkątnej. W programie wykorzystaj zdefiniowaną funkcję: trojkatna(n). Objaśnij działanie tej funkcji.
3. Zapisz program w pliku pod tą samą nazwą.

Zadania

1. Przedstaw obliczenia szóstej liczby Fibonacciego podobnie jak pokazano na rysunku 3. obliczenia czwartej liczby.
2. Zmodyfikuj program zapisany w ćwiczeniu 4., aby obliczał i wyświetlał w jednej kolumnie czterdzieści początkowych liczb Fibonacciego. Zapisz program w pliku pod nazwą Fibonacci_rekurencyjnie_40.
3. Napisz rekurencyjny program odliczający kolejno od 1 do n. (Dla n = 10 wynikiem ma być ciąg liczb: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10).
4. Napisz rekurencyjny program odliczający kolejno od n do 1. (Dla n = 10 wynikiem ma być ciąg liczb: 10, 9, 8, 7, 6, 5, 4, 3, 2 , 1).
5. Napisz rekurencyjny program sumujący elementy tablicy (listy).
6. Napisz rekurencyjny program wyznaczający liczbę cyfr liczby naturalnej.
7. Napisz rekurencyjny program obliczający sumę cyfr liczby naturalnej.
8. Napisz program wyznaczający wartość n-tego wyrazu ciągu określonego wzorem:
9.  

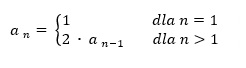
Dla zainteresowanych:

1. Napisz rekurencyjny program obliczający schematem Hornera wartość wielomianu
   W(x) = 3x³ + 2x² + 4x + 5. Współczynniki wielomianu przechowujemy w tablicy (liście). Dla danego przykładu będzie to tablica [ 3, 2, 4, 5 ].
2. Napisz rekurencyjny program wypisujący kolejne ruchy przenoszenia n krążków z palika A na palik B z wykorzystaniem palika pomocniczego P (tzw. łamigłówka Wież Hanoi). Program powinien również zliczać liczbę ruchów z odwołań rekurencyjnych (nie ze wzoru 2ⁿ – 1). Na rysunku 5. pokazano efekt działania programu dla trzech krążków.

Rys. 5. Efekt działania programu realizującego algorytm łamigłówki Wież Hanoi dla trzech krążków

1. Znajdź w Internecie informacje na temat równań diofantycznych. Zapoznaj się ze sposobem ich rozwiązywania.
2.  Znajdź w Internecie informacje na temat równań diofantycznych. Zapoznaj się ze sposobem ich rozwiązywania.