Rekurencyjna realizacja algorytmu Euklidesa i algorytmu szybkiego potęgowania liczb

Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

3. w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
4. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;

II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

2. sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

1. zapisuje za pomocą listy kroków lub pseudokodu i implementuje w wybranym języku programowania algorytmy poznane na wcześniejszych etapach oraz algorytmy:
   a) algorytm Euklidesa w wersji iteracyjnej i rekurencyjnej wraz z zastosowaniami,
   i) szybkiego potęgowania liczb w wersji iteracyjnej i rekurencyjnej,
3. objaśnia, a także porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przy tym przykłady problemów i algorytmów, w szczególności:
   a) wyszukiwanie elementów liniowe i przez połowienie (do znajdowania elementów w zbiorze, sortowania przez wstawianie, przybliżonego rozwiązywania równań),
   b) rekurencję (do generowania ciągów liczb, potęgowania, sortowania liczb, generowania fraktali),

Spis treści

1. Algorytm Euklidesa – realizacja rekurencyjna
   1. Wersja algorytmu Euklidesa z odejmowaniem
   2. Wersja algorytmu Euklidesa z resztą z dzielenia
2. Zastosowania algorytmu Euklidesa
   1. Zastosowanie algorytmu Euklidesa do przelewania wody
   2. Inne zastosowania algorytmu Euklidesa
3. Szybkie potęgowanie liczb
   1. Szybkie potęgowanie liczb – realizacja iteracyjna
   2. Szybkie potęgowanie liczb – realizacja rekurencyjna

1. Algorytm Euklidesa – realizacja rekurencyjna

W tym temacie omówimy rekurencyjną realizację algorytmu Euklidesa w dwóch wersjach – z odejmowaniem i z dzieleniem. Przedstawimy ten algorytm w postaci pseudokodu i zapiszemy rekurencyjne funkcje w językach C++ i Python.

Ćwiczenie 1. Przypominamy algorytm Euklidesa

Przypomnij sobie z tematu C9 (część I Materiału edukacyjnego), do czego służy algorytm Euklidesa oraz jak oblicza się NWD według tego algorytmu w obydwu wersjach – z odejmowaniem i z resztą z dzielenia.

 

1.1. Wersja algorytmu Euklidesa z odejmowaniem

Przykład 1. Rekurencyjna realizacja algorytmu Euklidesa – wersja z odejmowaniem

Zadanie: Znajdź największy wspólny dzielnik (NWD) dwóch niezerowych liczb naturalnych metodą rekurencyjną. Zastosuj algorytm Euklidesa w wersji z odejmowaniem.

Dane: Dwie niezerowe liczby naturalne: a, b.

Wynik: Wartość największego wspólnego dzielnika liczb a i b: NWD.

Pseudokod algorytmu
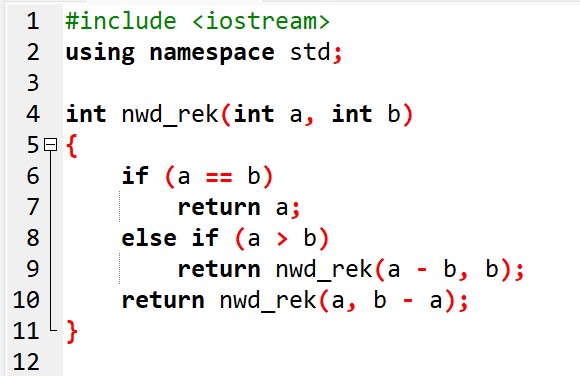
Zdefiniujemy funkcję nwd_rek() z dwoma parametrami (a i b  – oznaczającymi dwie liczby). W definicji funkcji następują jej wywołania wewnątrz niej samej. Funkcja zwraca wartość NWD równą a.

Definicja funkcji w języku programowania

Ćwiczenie 2. Piszemy program realizujący rekurencyjny algorytm Euklidesa w wersji z odejmowaniem

1. Napisz program realizujący rekurencyjny algorytm Euklidesa w wersji z odejmowaniem. Wykorzystaj funkcję zapisaną w pliku TC4_c1_Euklides_rek1.cpp lub w pliku TC4_c1_Euklides_rek1.py. Objaśnij działanie funkcji nwd_rek(), m.in. wskaż miejsca wywołań rekurencyjnych tej funkcji. 
2. Zapisz program w pliku pod tą samą nazwą.

1.1. Wersja algorytmu Euklidesa z resztą z dzielenia

Powtórka z matematyki

Załóżmy, że a ≥ b. Wtedy liczbę a możemy przedstawić następująco:

a = k · b + r,           gdzie    0  ≤ r < b                              [1.]

Jeśli liczba naturalna c dzieli liczbę a, to zgodnie z zasadami matematyki dzieli liczbę k · b + r, co z kolei oznacza, że dzieli k · b oraz r. Zatem:

 NWD(a, b) = NWD(b, r).

Na przykład, dla a = 28 i b = 8 zgodnie ze wzorem [1.] otrzymamy:

36 = 3 * 8 + 4 (k = 3, r = 4).  Zatem:

NWD(28, 8) = NWD(8, 4).

Przykład 2. Rekurencyjna realizacja algorytmu Euklidesa – wersja z resztą z dzielenia

Zadanie: Znajdź największy wspólny dzielnik (NWD) dwóch niezerowych liczb naturalnych metodą rekurencyjną. Zastosuj algorytm Euklidesa w wersji z resztą z dzielenia.

Dane: Dwie niezerowe liczby naturalne: a, b.

Wynik: Wartość największego wspólnego dzielnika liczb a i b: NWD.

Pseudokod algorytmu
Zdefiniujemy funkcję nwd_rek() z dwoma parametrami (a i b oznaczającymi dwie liczby). W definicji funkcji następuje jej wywołanie wewnątrz niej samej. Funkcja zwraca wartość NWD równą a.

Definicja funkcji w języku programowania

Ćwiczenie 3. Piszemy program realizujący rekurencyjny algorytm Euklidesa w wersji z resztą z dzielenia

1. Napisz program realizujący rekurencyjny algorytm Euklidesa w wersji z resztą z dzielenia. Wykorzystaj funkcję zapisaną w pliku TC4_c3_Euklides_rek2.cpp lub w pliku TC4_c3_Euklides_rek2.py. Objaśnij działanie funkcji nwd_rek(), m.in. wskaż miejsce wywołania rekurencyjnego tej funkcji.
2. Zapisz program w pliku pod tą samą nazwą.

2. Zastosowania algorytmu Euklidesa

2.1. Zastosowanie algorytmu Euklidesa do przelewania wody

Wśród zastosowań algorytmu Euklidesa znajduje się łamigłówka związana z wypełnianiem wodą naczynia o ustalonej objętości V za pomocą dwóch czerpaków o wybranych objętościach a, b. Musimy przyjąć, że naczynie, do którego mamy wlać ustaloną objętość wody V, musi mieć o wiele większą pojemność, niż objętość wody, jaka ma się w nim znaleźć. Dysponujemy również nieograniczoną ilością wody.

Zadanie napełniania naczynia dwoma czerpakami można zapisać w postaci następującego równania:

     [2.]

gdzie a i b oznaczają pojemności czerpaków, a V jest pojemnością wody, jaka ma się znaleźć w naczyniu; x oznacza liczbę ruchów czerpakiem a; y – liczbę ruchów czerpakiem b.

Z równania [2.] wynika, że jeśli dana liczba dzieli pojemności czerpaków a i b, to dzieli liczbę V. Największa taka liczba, czyli NWD (a, b), dzieli liczbę V.

Stąd otrzymujemy następujący wniosek: równanie [2.]  dla danych a, b i V ma rozwiązanie x i y, gdy V jest równe NWD(a, b) lub jest wielokrotnością NWD(a, b) (wtedy całą operację przelewania wody trzeba powtórzyć tyle razy, ile wynosi ta wielokrotność).

Przykład 3. Stosowanie algorytmu Euklidesa do przelewania wody

a = 6 litrów, b  = 8 litrów, V = 13 litrów.

NWD (6, 8) = 2                2 nie dzieli liczby 13.

Wniosek: czerpakami o pojemnościach 6 i 8 litrów nie można napełnić naczynia o pojemności 13 litrów.

Przykład 4. Stosowanie algorytmu Euklidesa do przelewania wody

a = 7 litrów, b = 9 litrów, V = 5 litrów.

NWD (7, 9) = 1                1 dzieli liczbę 5.

Wniosek: czerpakami o pojemnościach 7 i 9 litrów  można napełnić naczynie o pojemności 5 litrów.

Równanie [2.] ma postać:

i jego rozwiązaniem jest x = 2 oraz y = -1.

Rozwiązanie to należy odczytać w następujący sposób: 2 razy nalewamy wodę czerpakiem o pojemności 7 litrów i raz odlewamy wodę czerpakiem o pojemności 9 litrów.

Ćwiczenie 4. Znajdujemy rozwiązanie problemu przelewania wody dla przykładowych danych

Znajdź rozwiązanie problemu przelewania wody dla następujących danych: a = 12 litrów, b = 21 litrów, V = 9 litrów. Sprawdź najpierw, czy rozwiązanie jest możliwe.

2.2. Inne zastosowania algorytmu Euklidesa

Na informatyce w zakresie podstawowym pokazaliśmy zastosowanie algorytmu Euklidesa do:

• obliczenia najmniejszej wspólnej wielokrotności dwóch liczb (NWW) –  temat C4 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III” lub temat 87 z podręcznika „Informatyka 1-3. Podręcznik dla szkół ponadpodstawowych. Zakres podstawowy”,
• obliczenia wspólnej miary dwóch desek o zadanych wymiarach – temat 86 z podręcznika „Informatyka 1-3. Podręcznik dla szkół ponadpodstawowych. Zakres podstawowy”.

Algorytm Euklidesa możemy także zastosować do:

• obliczania maksymalnej długości boku kwadratu, którym można wypełnić w całości prostokąt o wymiarach a, b – ćwiczenie 5.,
• grupowania różnego rodzaju obiektów w zestawy – ćwiczenie 6.

Ćwiczenie 5. Piszemy program wyznaczający długość boku kwadratowego kawałka

1. Chcemy wykonać obrus o określonych wymiarach, szyjąc go z kwadratowych kawałków materiału. Napisz program wyznaczający największą możliwą długość boku kwadratowego kawałka oraz liczbę kawałków, których należy użyć, aby zszyć koronkowy obrus o zadanych wymiarach. W programie wykorzystaj jedną ze zdefiniowanych funkcji rekurencyjnych nwd_rek(a, b).
2. Zapisz program w pliku pod nazwą TC4_c5_obrus. Przetestuj program dla obrusa o bokach  180 cm x 120 cm.

Ćwiczenie 6. Piszemy program wyznaczający liczbę jednakowych zestawów składających się z dwóch obiektów

1. Napisz program wyznaczający liczbę jednakowych dwuskładnikowych zestawów nasion, które można przygotować ze 150 gramów nasion chabra bławatka oraz 60 gramów nasion maku polnego. Ile gramów każdego z nasion znajdzie się w jednym zestawie? W programie wykorzystaj jedną ze zdefiniowanych funkcji rekurencyjnych nwd_rek(a, b).
2. Zapisz program w pliku pod nazwą TC4_c6_zestaw_nasion.

3. Szybkie potęgowanie liczb

3.1. Szybkie potęgowanie liczb – realizacja iteracyjna

Matematycy już od starożytności zajmują się problematyką szybkiego potęgowania liczb, tzn. wykonywania tego zadania za pomocą jak najmniejszej liczby działań. W algorytmie naiwnym do  podniesienia x do potęgi n należy wykonać n – 1 operacji mnożenia, np. aby obliczyć x¹⁷, należy wykonać 16 operacji mnożenia

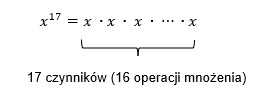
Wymyślono wiele różnych algorytmów, ale nie znaleziono jeszcze uniwersalnego algorytmu, który dla wszystkich wykładników wykonywałby potęgowanie za pomocą najmniejszej liczby działań. Jednym z algorytmów szybkiego podnoszenia do potęgi jest algorytm wykorzystujący binarne rozwinięcie wykładnika potęgi. Pozwala ono na zredukowanie liczby operacji mnożenia.

17 = 16 + 1 = 2⁴ + 2⁰  = 10001₂         zatem x¹⁷ = x¹⁰⁰⁰¹₂ = x¹⁶ • x¹
x² = x • x            (1 mnożenie)
x⁴ = x² • x²        (1 mnożenie)
x⁸ = x⁴ • x⁴        (1 mnożenie)
x¹⁶ = x⁸ • x⁸      (1 mnożenie)
x¹⁷ = x¹⁶ • x¹    (1 mnożenie)
Ostatecznie wykonamy 5 operacji mnożenia:

Przykład 5. Iteracyjna realizacja szybkiego potęgowania liczb

Zadanie:  Oblicz wartość n-tej potęgi liczby x metodą iteracyjną.
Dane:  Wykładnik potęgi n – liczba całkowita nieujemna, n ≥ 0.
Wynik: Wartość potęgi x ⁿ, zapisana w zmiennej y.

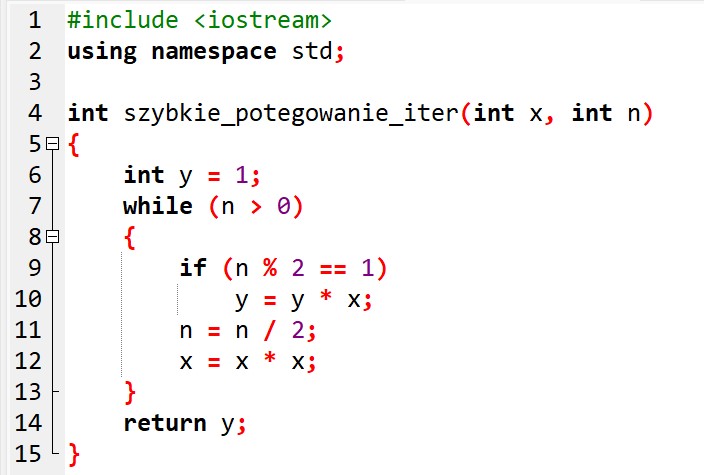
Pseudokod algorytmu

Uwaga: W pseudokodzie zapis typu y ⟵ 1 oznacza przypisane zmiennej po lewej stronie strzałki wartości po prawej stronie strzałki.

Definicja funkcji w języku programowania

Ćwiczenie 7. Piszemy program szybkiego podnoszenia do potęgi w wersji iteracyjnej

1. Napisz program realizujący rekurencyjny algorytm Euklidesa w wersji z resztą z dzielenia. wyznaczający n-tą potęgę liczby x . W programie wykorzystaj zdefiniowaną funkcję  szybkie_potegowanie_iter(x, n) zapisaną w pliku TC4_c7_szybkie_potegowanie_iter.cpp lub w pliku TC4_c7_szybkie_potegowanie_iter.py. Objaśnij działanie funkcji szybkie_potegowanie_iter(), m.in.
   uzasadnij użycie instrukcji while, a wewnątrz niej instrukcji if.
2. Napisz program wyznaczający n-tą potęgę liczby x . W programie wykorzystaj zdefiniowaną funkcję  szybkie_potegowanie_iter(x, n). Ile wyniesie 2 podniesione do potęgi 19?
3. Zapisz program w pliku pod nazwą TC4_c7_szybkie_potegowanie.

3.2. Szybkie potęgowanie liczb – realizacja rekurencyjna

Rozpatrzmy dwa przypadki – pierwszy dla wykładnika parzystego n = 8, drugi dla wykładnika nieparzystego n = 9.

• Przypadek pierwszy – wykładnik parzysty n = 8
  x⁸ = (x⁴)² = (x ^{(8 div 2)})²
• Przypadek drugi – wykładnik nieparzysty n = 9
  x⁹ = (x⁴)² · x = (x ^{(9 div 2)})² · x

Po prawej stronie otrzymaliśmy znów potęgi z wykładnikiem parzystym lub nieparzystym, taki sposób postępowania można wyrazić wzorem rekurencyjnym:

Przykład 6. Rekurencyjna realizacja szybkiego potęgowania liczb

Zadanie:  Oblicz wartość n-tej potęgi liczby x metodą rekurencyjną.

Dane:  Wykładnik potęgi n – liczba całkowita nieujemna, n ≥ 0.

Wynik: Wartość potęgi x ⁿ, zapisana w zmiennej y.

Pseudokod algorytmu

Definicja funkcji w wybranym języku programowania

Ćwiczenie 8. Piszemy program szybkiego podnoszenia do potęgi w wersji rekurencyjnej

1. Napisz program wyznaczający n-tą potęgę liczby x metodą rekurencyjną. W programie wykorzystaj funkcję  szybkie_potegowanie_rek(x, n) zapisaną w pliku TC4_c8_szybkie_potegowanie_rek.cpp lub w pliku TC4_c8_szybkie_potegowanie_rek.py. Objaśnij działanie funkcji szybkie_potegowanie_rek(), m.in. wskaż miejsca wywołania rekurencyjnego funkcji.
2. Zapisz program w pliku pod tą samą nazwą.

Zadania

1. Przedstaw schemat wywołań rekurencyjnych funkcji nwd_rek() dla wybranych liczb a i b, podobnie jak pokazano to dla obliczeń silni metodą rekurencyjną w temacie C3 w podręczniku „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa III” lub w temacie 95, w podręczniku „Informatyka 1-3. Podręcznik dla szkoły ponadpodstawowej. Zakres podstawowy”. 
2. Napisz rekurencyjny program wypisujący na ekranie n gwiazdek (lub innego znaku wprowadzonego z klawiatury).