Temat C4. Sito Eratostenesa i rozkład liczby na czynniki pierwsze – realizacja w językach C++ i Python

Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.

Uwaga: Zapoznaj się wcześniej z tematem C3 z podręcznika „Teraz bajty. Informatyka dla szkół ponadpodstawowych. Zakres podstawowy. Klasa II” lub tematami 63 i 75 z podręcznika „Informatyka 1-3. Podręcznik dla szkoły ponadpodstawowej. Zakres podstawowy” Wykonaj zawarte tam ćwiczenia i zadania.

Zapisy podstawy programowej realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
2) do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1) zapisuje za pomocą listy kroków, schematu blokowego lub pseudokodu, i implementuje w wybranym języku programowania, algorytmy poznane na wcześniejszych etapach oraz algorytmy:
c) generowania liczb pierwszych metodą sita Eratostenesa,
2) wykorzystuje znane sobie algorytmy przy rozwiązywaniu i programowaniu rozwiązań następujących problemów:
a) rozkładania liczby na czynniki pierwsze

Spis treści

1. Generowanie liczb pierwszych metodą sita Eratostenesa
2. Rozkład liczby na czynniki pierwsze
3. Liczby doskonałe

1. Generowanie liczb pierwszych metodą sita Eratostenesa

Ćwiczenie 1. Przypominamy algorytm badania pierwszości liczby

Przypomnij algorytm badania pierwszości liczby omówiony na lekcji informatyki realizowanej w zakresie podstawowym. Korzystając z tego algorytmu, sprawdź, czyli liczby 13 i 32 są liczbami pierwszymi.

Wynalazcą algorytmu jest grecki matematyk, Eratostenes z Cyreny, żyjący na przełomie II i III w. p.n.e. Zauważył on, że liczby niepierwsze są wielokrotnościami kolejnych liczb pierwszych (np. 4, 6, 8, 10, … są wielokrotnościami 2; natomiast 3, 6, 9, 12, … są wielokrotnościami 3 itd.). Wystarczy więc z tablicy wszystkich liczb naturalnych wykreślić kolejno: wielokrotności 2, z liczb, które pozostaną, wielokrotności 3, potem wielokrotności 5 (wykreślając wielokrotności 2, wykreśliliśmy już wielokrotności 4), potem wielokrotności 7 (wykreślając wielokrotności 2 i 3, wykreśliliśmy wielokrotności 6) itd. Łatwo zauważyć, że wykreślamy wielokrotności kolejnych, już uzyskanych liczb pierwszych. Liczby, które pozostaną w tablicy, są liczbami pierwszymi.

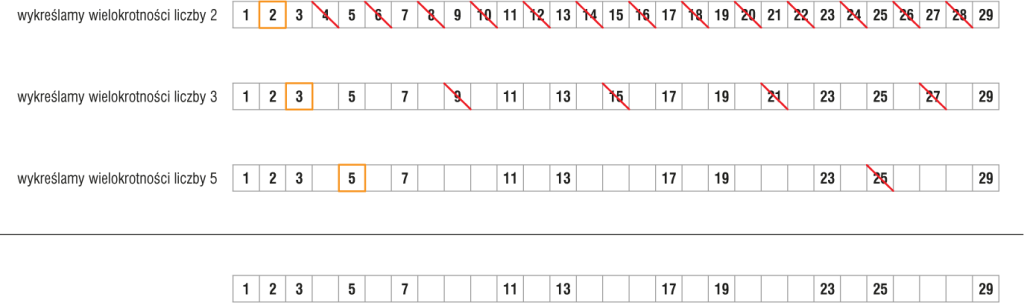
Na rysunku 1. pokazano działanie sita Eratostenesa. W kolejnych przejściach algorytmu (odpowiadających kolejnym wierszom rysunku) wykreślamy wielokrotności liczb pierwszych. W pierwszym przejściu wykreślamy wielokrotności liczby 2, w drugim – 3, w trzecim 5. Liczby wykreślone w poprzednich przejściach usunięto, a pozostałe liczby (widoczne w ostatnim wierszu rysunku) są liczbami pierwszymi.

W praktyce do realizacji algorytmu można wykorzystać tablicę (lub listę), w której będziemy pamiętać, czy dana liczba jest liczbą pierwszą, czy złożoną. Tablicę (listę) tę przeglądamy, zaznaczając jako niepierwsze kolejne wielokrotności liczb pierwszych.

Przykład 1. Realizacja algorytmu generowania liczb pierwszych metodą sita Eratostenesa w języku C++ i Python

Zadanie: Napisz program, który umożliwi wyprowadzenie na ekran monitora liczby pierwsze nie większe od n metodą sita Eratostenesa.

Dane: liczba naturalna dodatnia n.

Wynik: liczby pierwsze nie większe od n zapamiętywane jako elementy tablicy sito[].

Fragmenty programów realizujących algorytm generowania liczb pierwszych metodą sita Eratostenesa pokazano w przykładzie 1. (w języku C++) i przykładzie 2. (w języku Python).

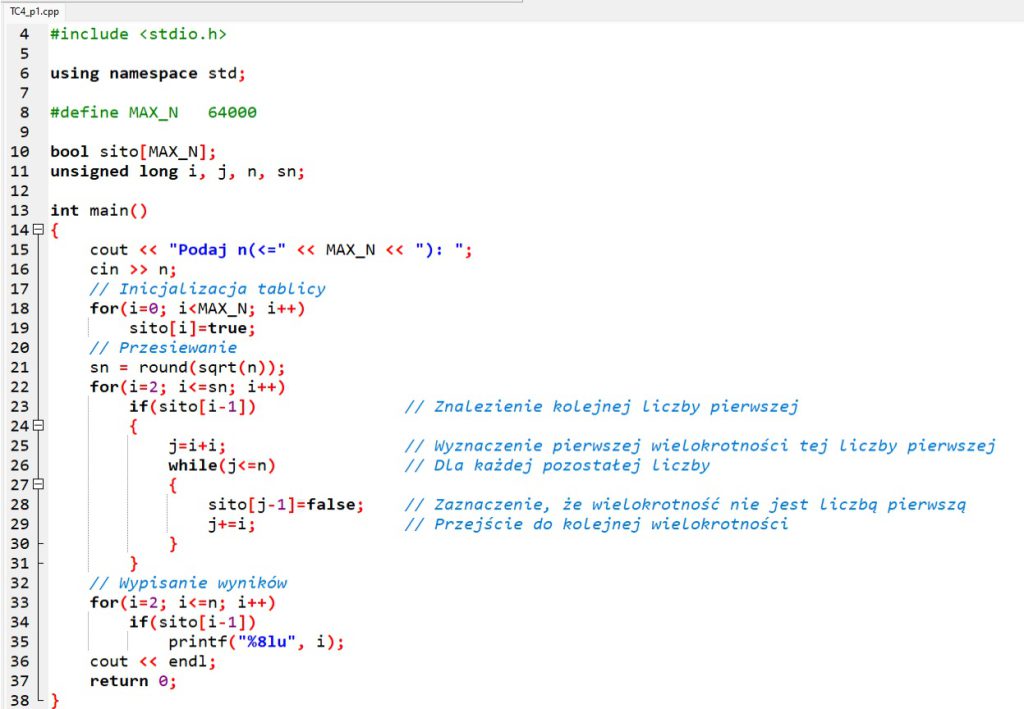
W języku C++ najważniejszą część algorytmu realizuje pętla for. W pętli tej sprawdzamy, czy liczba na pozycji i jest liczbą pierwszą: if(sito[i-1]). Jeżeli tak, to wykreślamy jej wielokrotności nie większe od n – pętla while(j<=n). Proces powtarzamy dla liczb od 2 do pierwiastka kwadratowego z n, jak już bowiem wcześniej ustaliliśmy, liczba złożona n ma dzielniki nie większe od jej pierwiastka kwadratowego. Łatwo zauważyć, że algorytm ten nie wymaga wykonywania operacji dzielenia, a jego złożoność obliczeniowa jest rzędu O(n • log₂log₂n).

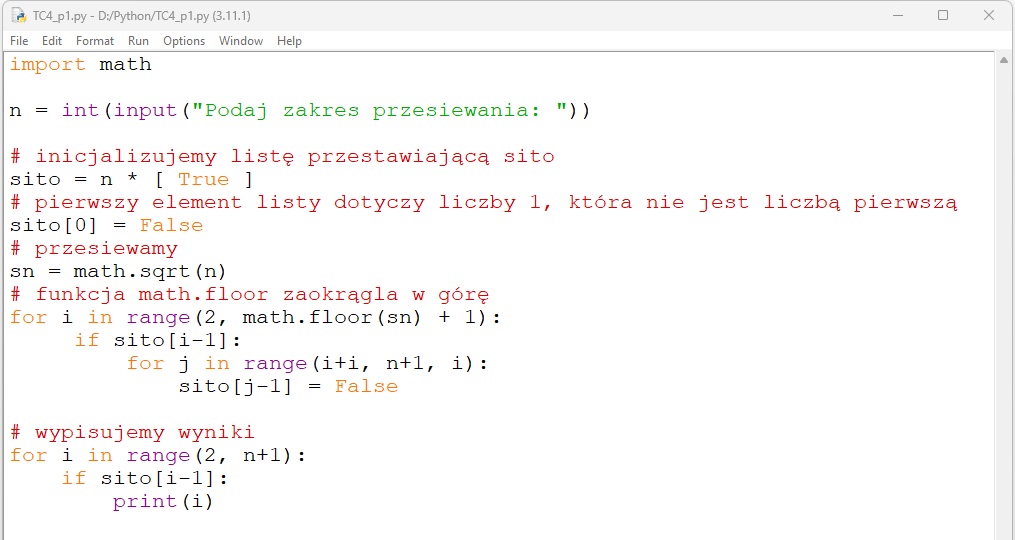
W języku Python posługujemy się funkcją range(początek, koniec), która zwraca sekwencję liczb (start, początek+1, …, koniec-1). Stąd jako koniec ustawiamy np. n+1. Używamy również innego wariantu tej funkcji: range(początek, koniec, krok), aby oznaczyć wielokrotności kroku jako liczby złożone.

Ćwiczenie 2. Analizujemy program realizujący algorytm generowania liczb pierwszych metodą sita Eratostenesa

1. Otwórz plik lub TC4_p1.cpp lub TC4_p1.py.
2. Zapoznaj się z pełnym kodem programu. Objaśnij działanie poszczególnych wierszy programu. Przeanalizuj wstawione do kodu komentarze.
3. Uruchom program i wykonaj go dla przykładowych danych.

2. Rozkład liczby na czynniki pierwsze

Na przykład czynnikami pierwszymi liczby 20 są: 2, 2 i 5, natomiast liczba 17 ma jeden czynnik pierwszy, równy 17.
Na przykład: 20 = 2 · 2 · 5 = 2² · 5,
248 = 2 · 2 · 2 · 31 = 2³ · 31.
Czynnik pierwszy danej liczby naturalnej to dowolna liczba pierwsza, która dzieli tę liczbę.

Podstawowym sposobem rozkładu liczby na czynniki pierwsze jest jej dzielenie przez kolejne liczby pierwsze. Wykonajmy rozkład liczby 56 na czynniki pierwsze. Szukamy najmniejszej liczby pierwszej, dzielącej daną liczbę (56). Jest to 2. Dzielimy: 56 : 2 = 28.

Powtarzamy tę czynność dla kolejnych wyników aż do uzyskania w ilorazie liczby 1.

Otrzymujemy wówczas wszystkie dzielniki pierwsze szukanej liczby. Na schemacie znajdują się one po prawej stronie.

56 |2
28 |2
14 |2
  7 |7
1 |

Opis algorytmu

Przyjmiemy oznaczenia: n – dana liczba; c – liczba pierwsza; c₁, c₂, …, c_k – czynniki pierwsze liczby n.

Dzielimy n przez kolejne liczby pierwsze c: 2, 3, 5, 7, 11, 13… itd. Jeśli napotkamy taką liczbę c, że n będzie przez nią podzielne (czyli n % c = 0), to c będzie najmniejszym dzielnikiem n, czyli czynnikiem c₁. Natomiast wynik dzielenia liczby n przez znalezioną liczbę pierwszą c będzie nową liczbą n.

Następnie dzielimy tak wyliczone nowe n przez kolejne liczby pierwsze, zaczynając od c (należy pamiętać, że c może wystąpić wielokrotnie w rozkładzie liczby na czynniki pierwsze).

Algorytm kończy się, gdy dla kolejnego c liczba n nie jest podzielna przez c i część całkowita ilorazu (n/c)(n/c) nie jest większa niż c. Oznacza to, że ostatnie wyliczone n jest liczbą pierwszą, a tym samym jest równe ostatniemu czynnikowi pierwszemu (c_k ).

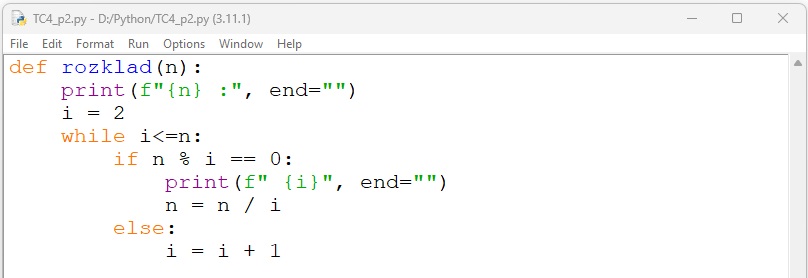
Przykład 2. Realizacja algorytmu rozkładu liczby na czynniki pierwsze w językach C i Python

Zadanie: Napisz funkcję wyprowadzającą na ekran monitora wszystkie czynniki pierwsze liczby n.

Dane: Liczba naturalna n, gdzie n > 1.

Wynik: Wszystkie czynniki pierwsze liczby a: c₁, c₂,…, c_k.

Funkcja rozkład() sprawdza wszystkie dzielniki (nie tylko pierwsze) liczby n. Kod jest wówczas uproszczony, ale złożoność obliczeniowa pozostaje taka sama.

Ćwiczenie 3. Analizujemy program realizujący algorytm rozkładu na czynniki pierwsze

1. Otwórz plik lub TC4_p2.cpp lub TC4_p2.py. W plikach zapisano program realizujący algorytm rozkładu na czynniki pierwsze liczby podanej przez użytkownika.
2. Objaśnij działanie poszczególnych wierszy funkcji i programu głównego. Uruchom program. Wykonaj program dla przykładowych danych.

3. Liczby doskonałe

Na przykład liczba 6 jest liczbą doskonałą, ponieważ 1 + 2 + 3 = 6. Następną liczbą doskonałą jest 28 (28 = 14 + 7 + 4 + 2 + 1), a kolejne to 496, 8128, 33550336, 8589869056

i 137438691328.

Aby sprawdzić, czy dana liczba jest liczbą doskonałą, należy znaleźć wszystkie jej dzielniki różne od niej samej, zsumować je i sprawdzić, czy obliczona suma jest równa tej liczbie.

Opis algorytmu

Przyjmiemy oznaczenia: x – dana liczba; SumaD – suma dzielników; d – dzielnik liczby x.

Aby znaleźć wszystkie dzielniki liczby x, wystarczy sprawdzać, czy wszystkie liczby od 1 do (x/2)(x/2) są dzielnikami danej liczby.

Na początku przyjmujemy, że SumaD jest równa zero, a d jest równe jeden. Ponieważ x % 1 = 0 (czyli 1 jest pierwszym dzielnikiem liczby x), to SumaD jest równa 1 (SumaD := SumaD + d). Powtarzamy postępowanie dla d zwiększonego o jeden, czyli dla i = 2. Sprawdzamy, czy x % 2 = 0. Jeśli tak, dodajemy do zmiennej SumaD wartość kolejnego dzielnika (liczbę 2), jeśli nie – zwiększamy d o jeden i powtarzamy sprawdzanie podzielności liczby x przez kolejny dzielnik.

Algorytm kończy się, gdy d > x/2. Na koniec sprawdzamy, czy x = SumaD. Jeśli tak, x jest liczbą doskonałą.

Przykład 3. Sprawdzanie, czy liczba x jest liczbą doskonałą

Sprawdzimy, czy liczba x = 6 jest liczbą doskonałą.

Obliczmy: x/2=(6/2)(x/2)=6/2=3
SumaD = 0; d = 1
czy 1 <= 3?                                         TAK
czy 6 % 1 = 0?                                   TAK
SumaD = 0 + 1 = 1; d = 2
czy 2 <= 3?                                         TAK
czy 6 % 2 = 0?                                   TAK
SumaD = 1 + 2 = 3; d = 3
czy 3 <= 3?                                         TAK
czy 6 % 3 = 0?                                   TAK
SumaD = 3 + 3 = 6; d = 4
czy 4 <= 3?                                          NIE
czy SumaD = x? czy 6 = 6?            TAK     6 jest liczbą doskonałą.

Ćwiczenie 4. Sprawdzamy, czy dana liczba jest liczba doskonałą

Korzystając z podanego opisu i przykładu 12., sprawdź, czy liczby 9 i 28 są liczbami doskonałymi. Znajdź w Internecie więcej informacji na temat liczb doskonałych.

Ćwiczenie 5. Piszemy specyfikację zadania i listę kroków algorytmu sprawdzania, czy dana liczba jest liczbą doskonałą

Napisz specyfikację zadania, utwórz listę kroków oraz narysuj schemat blokowy algorytmu sprawdzania, czy dana liczba jest liczbą doskonałą.

Zadania

1. Napisz specyfikację zadania i program wypisujący wszystkie liczby pierwsze występujące w zadanym przez użytkownika przedziale. Wykorzystaj plik TC4_p1.cpp lub TC4_p1.py.
2. Zmodyfikuj program zapisany w pliku TC4_p1.cpp lub w pliku TC4_p1.py, aby algorytm Sita Eratostenesa był zrealizowany z wykorzystaniem funkcji przesiej() przesiewającej liczby zgodnie z algorytmem Sita Eratostenesa i wypisz() wypisującą przesiane liczby pierwsze na ekran.

3. Napisz program wyprowadzający na ekran monitora wszystkie czynniki pierwsze dla liczb z podanego przez użytkownika przedziału. Wykorzystaj plik TC4_p2.cpp lub TC4_p2.py.
4. Napisz program sprawdzający, czy dana liczba jest liczbą doskonałą.

Dla zainteresowanych

5. Narysuj schemat blokowy algorytmu generowania liczb pierwszych metodą sita Eratostenesa.
6. Napisz listę kroków algorytmu rozkładu liczby na czynniki pierwsze.
7. Napisz program znajdujący n kolejnych par liczb bliźniaczych, zaczynając od pary (3, 5). Do sprawdzania, czy liczba jest pierwsza, użyj algorytmu Sita Eratostenesa, którego realizację zapisaliśmy w plikach TC4_p1.cpp i TC4_p1.py.

8. Znajdź w Internecie informacje o największej znalezionej dotąd liczbie pierwszej. Na czym polega rola liczb pierwszych w kryptografii?
9. Napisz program rozkładający liczbę naturalną na czynniki pierwsze z wykorzystaniem algorytmu sita Eratostenesa.