Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.
Zapisy podstawy programowej 2024 realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
- ilustruje i wyjaśnia rolę pojęć, obiektów i operacji matematycznych w projektowaniu rozwiązań problemów informatycznych i z innych dziedzin, posługuje się pojęciem logarytmu;
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- przygotowując opracowania rozwiązań złożonych problemów, posługuje się wybranymi aplikacjami w stopniu zaawansowanym:
b) stosuje zaawansowane funkcje arkusza kalkulacyjnego w zależności od rodzaju danych,
Spis treści
- Wybrane funkcje arkusza kalkulacyjnego
- Funkcje statystyczne
- Funkcje matematyczne
- Funkcje tekstowe
- Przedstawianie zależności funkcyjnych w arkuszu kalkulacyjnym
- Wykres funkcji liniowej
- Wykres wielomianu
- Wykres funkcji trygonometrycznej
- Wykres funkcji logarytmicznej
1. Wybrane funkcje arkusza kalkulacyjnego
1.1. Funkcje statystyczne
Funkcja ILE.LICZB(zakres_komórek) lub ILE.LICZB(wartość1;wartość2;…) oblicza, ile komórek zawierających liczby jest na liście argumentów.
Wśród argumentów funkcji ILE.LICZB mogą występować różne typy danych, ale zliczane są tylko liczby, daty lub tekstowe reprezentacje liczb (np. liczby zapisane w cudzysłowie). Inne wartości są pomijane (np. tekst, puste komórki).
![]() Przykład 1. Stosowanie funkcji ILE.LICZB
Przykład 1. Stosowanie funkcji ILE.LICZB
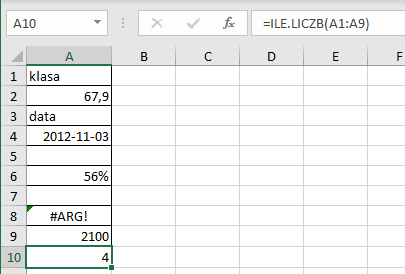
W arkuszu przedstawionym na rysunku 1. wartością formuły =ILE.LICZB(A1:A9) jest liczba 4. Liczby wpisano do czterech komórek: A2, A4, A6 i A9.
Wartością formuły =ILE.LICZB(A1:A9;10;20;30) jest liczba 7, ponieważ zliczono również trzy liczby (10, 20, 30) występujące jako argumenty.
Uwagi:
- Data również jest traktowana jak liczba.
- Komórki puste oraz zawierające błąd (np. #ARG!) są pomijane.
![]() Ćwiczenie 1. Stosujemy funkcję ILE.LICZB
Ćwiczenie 1. Stosujemy funkcję ILE.LICZB
- Otwórz plik TB2_c1_Liczby.xls. W tabeli przedstawiono wykaz godzin przepracowanych przez pracowników pewnej firmy w ciągu tygodnia oraz wykaz nieobecności pracowników z podaniem przyczyny.
- Oblicz, ile dni poszczególni pracownicy przepracowali w ciągu tygodnia oraz ilu pracowników było obecnych każdego dnia.
- Zapisz plik pod tą samą nazwą.
Wartością funkcji ILE.NIEPUSTYCH(zakres_komórek) lub ILE.NIEPUSTYCH(wartość1;wartość2;…) jest liczba komórek, które nie są puste.
![]() Przykład 2. Stosowanie funkcji ILE.NIEPUSTYCH
Przykład 2. Stosowanie funkcji ILE.NIEPUSTYCH
W arkuszu przedstawionym na rysunku 1. wartością formuły =ILE.NIEPUSTYCH(A1:A9) jest liczba 7.
W zakresie komórek od A1 do A9 dwie komórki – A5 i A7 – są puste.
![]() Ćwiczenie 2. Stosujemy funkcję ILE.NIEPUSTYCH
Ćwiczenie 2. Stosujemy funkcję ILE.NIEPUSTYCH
- Otwórz plik TB2_c2_Lista_obecności.xls. W tabeli przedstawiono wykaz nieobecności uczniów pewnej klasy w ciągu tygodnia, z podaniem przyczyny.
- Oblicz, ile dni byli nieobecni poszczególni uczniowie w ciągu tygodnia oraz ilu uczniów było obecnych każdego dnia.
- Zapisz plik pod tą samą nazwą.
Wartością funkcji ŚREDNIA.JEŻELI (zakres_komórek;kryterium;srednia_zakres) jest średnia arytmetyczna z wartości umieszczonych w komórkach z podanego zakresu i spełniających podany warunek.
Jako zakres należy podać zakres komórek, których wartości będą sprawdzane pod kątem spełniania kryterium. Srednia_zakres to rzeczywisty zestaw komórek, dla których będzie liczona średnia. Jeżeli nie zostanie podany, obliczenia zostaną wykonane dla komórek określonych przez argument zakres.
![]() Przykład 3. Stosowanie funkcji ŚREDNIA.JEŻELI
Przykład 3. Stosowanie funkcji ŚREDNIA.JEŻELI
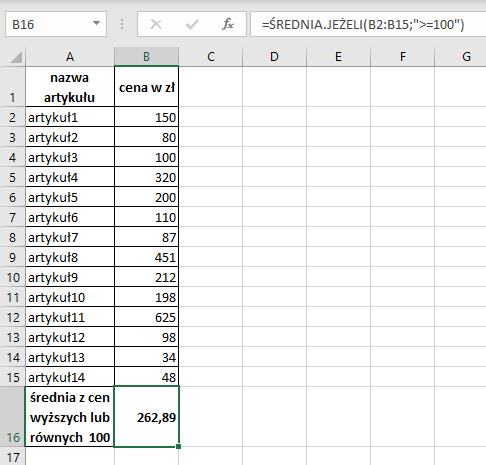
W arkuszu przedstawionym na rysunku 2. formuła umieszczona w komórce B16 =ŚREDNIA.JEŻELI(B2:B15;”>=100″) oblicza średnią cenę artykułów, których cena (umieszczona w komórkach B2:B15) jest równa lub wyższa od 100 zł. Średnią cenę obliczono dla wartości z komórek: B2, B5, B6, B7, B9, B10, B11, B12.
Trzeci argument funkcji (srednia_zakres) można pominąć.
![]() Ćwiczenie 3. Stosujemy funkcje LICZ.JEŻELI i ŚREDNIA.JEŻELI
Ćwiczenie 3. Stosujemy funkcje LICZ.JEŻELI i ŚREDNIA.JEŻELI
- Otwórz plik TB2_c3_Wyniki studentów.xls.
- Oblicz, ilu uczniów otrzymało z egzaminu powyżej 30 punktów. Wynik wyświetl w komórce B83.
- Oblicz średnią ocen z egzaminu dla studentów, którzy otrzymali powyżej 30 punktów. Wynik wyświetl w komórce B84.
- Zapisz plik pod tą samą nazwą
1.2. Funkcje matematyczne
Funkcja SUMA.JEŻELI sumuje wartości spełniające podane kryteria. Funkcja ma postać SUMA.JEŻELI(zakres;kryterium) lub SUMA.JEŻELI(zakres;kryterium;zakres_sumowania).
Jako zakres należy podać zakres komórek, których wartości będą sprawdzane pod kątem spełniania kryterium. Zakres_sumowania to zakres komórek, których wartości chcemy zsumować; jeżeli nie zostanie podany, sumowane będą komórki określone przez argument zakres.
![]() Przykład 4. Stosowanie funkcji SUMA.JEŻELI
Przykład 4. Stosowanie funkcji SUMA.JEŻELI
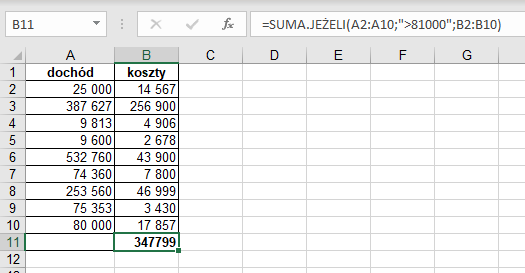
W arkuszu przedstawionym na rysunku 4. wartością formuły =SUMA.JEŻELI(A2:A10;”>81000″;B2:B10) jest liczba 347799. Zsumowano wartości tych komórek z kolumny B, dla których odpowiadające wartości w kolumnie A są większe od 81000 (czyli zsumowano wartości z komórek B3, B6, B8).
![]() Ćwiczenie 4. Stosujemy funkcję SUMA.JEŻELI
Ćwiczenie 4. Stosujemy funkcję SUMA.JEŻELI
- Otwórz plik TB2_c4_Koszty.xls. W komórce B25 utwórz formułę obliczającą łączne koszty uzyskania przychodów powyżej 25 000 zł.
- Zapisz plik pod tą samą nazwą.
Do rozwiązywania zadań z kombinatoryki i rachunku prawdopodobieństwa użyteczne są funkcje SILNIA i KOMBINACJE.
Funkcja SILNIA(n) oblicza wartość silni danej liczby naturalnej n. Silnię z liczby naturalnej n definiujemy następująco:
![]()
![]() Przykład 5. Stosowanie funkcji SILNIA
Przykład 5. Stosowanie funkcji SILNIA
Wartością formuły =SILNIA(5) jest liczba 120. Jest to wartość iloczynu kolejnych liczb naturalnych z przedziału od 1 do 5.
![]() Ćwiczenie 5. Stosujemy funkcję SILNIA
Ćwiczenie 5. Stosujemy funkcję SILNIA
- Wprowadź do kolumny A dwadzieścia liczb naturalnych od 1 do 20, a w kolumnie B obliczaj i wyświetlaj silnię tych liczb.
- Zapisz plik pod nazwą TB2_c5_Silnia.
Funkcja KOMBINACJE(n;k) podaje wartość symbolu Newtona dla pary liczb naturalnych n i k.
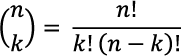
![]() Ćwiczenie 6. Stosujemy funkcję KOMBINACJE
Ćwiczenie 6. Stosujemy funkcję KOMBINACJE
- Symbol Newtona wyraża liczbę k-elementowych podzbiorów w zbiorze n-elementowym, np. dwoje dzieci można wybrać spośród pięciu na sposobów.
Korzystając z arkusza kalkulacyjnego, oblicz, na ile sposobów można wybrać dwuosobową reprezentację spośród 25 uczniów jednej klasy. - Zapisz plik pod nazwą TB2_c6.
1.3. Funkcje tekstowe
Wartością funkcji PRAWY(tekst;liczba_znaków) jest ciąg znaków o długości liczba_znaków wzięty z końca tekstu tekst.
Funkcja PRAWY należy do kategorii funkcji tekstowych. Pominięcie argumentu liczba_znaków oznacza, że jako jego wartość zostanie przyjęta liczba 1, czyli wynikiem funkcji będzie ostatnia litera tekstu. Jeśli wartość argumentu liczba_znaków jest większa od długości tekstu, funkcja zwraca cały tekst.
![]() Przykład 6. Stosowanie funkcji PRAWY
Przykład 6. Stosowanie funkcji PRAWY
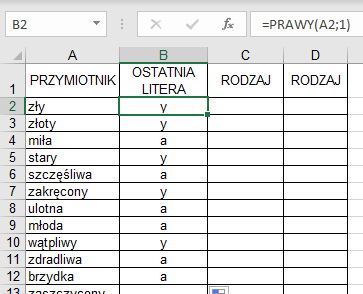
W arkuszu przedstawionym na rysunku 4. formuła =PRAWY(A2;1) wyświetla w komórce B2 literę y. Jest to ostatnia litera tekstu umieszczonego w komórce A2.
![]() Ćwiczenie 7. Stosujemy funkcję PRAWY
Ćwiczenie 7. Stosujemy funkcję PRAWY
- Otwórz plik TB2_c7_Przymiotniki.xls – w tabeli zapisano przymiotniki rodzaju męskiego i żeńskiego. W komórce B2 wyświetl ostatnią literę danego wyrazu.
- W komórkach C2 i D2 utwórz formuły, które wyświetlą rodzaj przymiotników zapisanych w kolumnie A. Ćwiczenie rozwiąż dwoma sposobami:
- W komórce C2 umieść formułę wykorzystującą funkcję logiczną JEŻELI oraz wynik uzyskany w komórce B2. Skopiuj gotową formułę do pozostałych komórek w kolumnie C.
- W komórce D2 umieść formułę wykorzystującą funkcję logiczną JEŻELI, w której jako test logiczny umieść funkcję tekstową PRAWY, badającą ostatni znak tekstu w komórce A2. Jeśli będzie to „y”, powinien być wyświetlany napis męski, w przeciwnym wypadku – napis żeński. Skopiuj gotową formułę do pozostałych komórek w kolumnie D. Sprawdź, czy w kolumnach C i D pojawiły się jednakowe wyniki.
- Zapisz plik pod tą samą nazwą.
Wartością funkcji FRAGMENT.TEKSTU(tekst;numer_pierwszego_znaku;liczba_znaków) jest ciąg znaków składający się z liczby_znaków wziętych z tekstu, począwszy od znaku o numerze numer_pierwszego_znaku. Znaki numerowane są od 1.
W przypadku, gdy numer_pierwszego_znaku jest większy niż liczba znaków w tekście, wynikiem funkcji jest pusty ciąg znaków. W przypadku, gdy numer_pierwszego_znaku jest mniejszy niż liczba znaków w tekście oraz suma numeru_pierwszego_znaku i liczby_znaków przewyższa liczbę znaków w tekście, wynikiem funkcji jest ciąg znaków od znaku o numerze numer_pierwszego_znaku do końca tekstu.
![]() Przykład 7. Stosowanie funkcji FRAGMENT.TEKSTU
Przykład 7. Stosowanie funkcji FRAGMENT.TEKSTU
W komórce A1 umieszczono napis urządzenia mobilne.
Formuła =FRAGMENT.TEKSTU(A1;12;7) wyświetli napis mobilne.
Formuła =FRAGMENT.TEKSTU(A1;2;4) wyświetli napis rząd.
Uwaga: Spacja również jest liczona jako znak.
![]() Ćwiczenie 8. Stosujemy funkcję FRAGMENT.TEKSTU
Ćwiczenie 8. Stosujemy funkcję FRAGMENT.TEKSTU
- W nowym arkuszu, w komórce A1 umieść napis drukarka laserowa. Wprowadź do komórki D1 formułę, która wyświetli w tej komórce napis druk, a do komórki E2 – formułę, która wyświetli w niej napis las.
- Zapisz plik pod nazwą Fragment.
![]() Przykład 8. Stosowanie funkcji DŁ
Przykład 8. Stosowanie funkcji DŁ
Aby wyświetlić przedostatnią literę w ciągu znaków, można posłużyć się funkcją DŁ, zagnieżdżoną w funkcji FRAGMENT.TEKSTU.
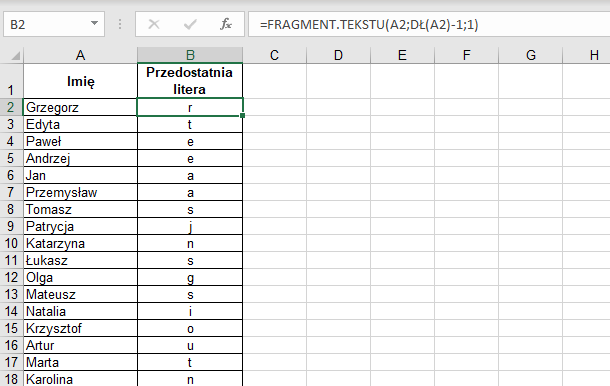
Na rysunku 5. formuła =FRAGMENT.TEKSTU(A2;DŁ(A2)-1;1) wyświetli literę r.
![]() Ćwiczenie 9. Stosujemy funkcję DŁ
Ćwiczenie 9. Stosujemy funkcję DŁ
- Otwórz plik TB2_c9_Imiona.xls. W kolumnie B utwórz formułę, która wyświetli trzecią literę od końca każdego imienia zapisanego w kolumnie A.
- Zapisz plik pod tą samą nazwą.
2. Przedstawianie zależności funkcyjnych w arkuszu kalkulacyjnym
Aby przedstawić zależności funkcyjne w arkuszu kalkulacyjnym, należy wprowadzić do komórek tabeli wartości argumentów funkcji oraz niezbędne współczynniki, a następnie utworzyć formułę do obliczania wartości funkcji.
Korzystając z możliwości arkusza kalkulacyjnego, można sporządzić również wykres funkcji. Do zobrazowania zależności funkcyjnych najlepiej zastosować wykres typu XY (punktowy), który umożliwia wyświetlenie serii danych w postaci punktów w układzie współrzędnych.
Przy sporządzaniu wykresów funkcji należy odpowiednio dobrać zakres argumentów oraz ich ilość (odstępy między nimi).
2.1. Wykres funkcji liniowej
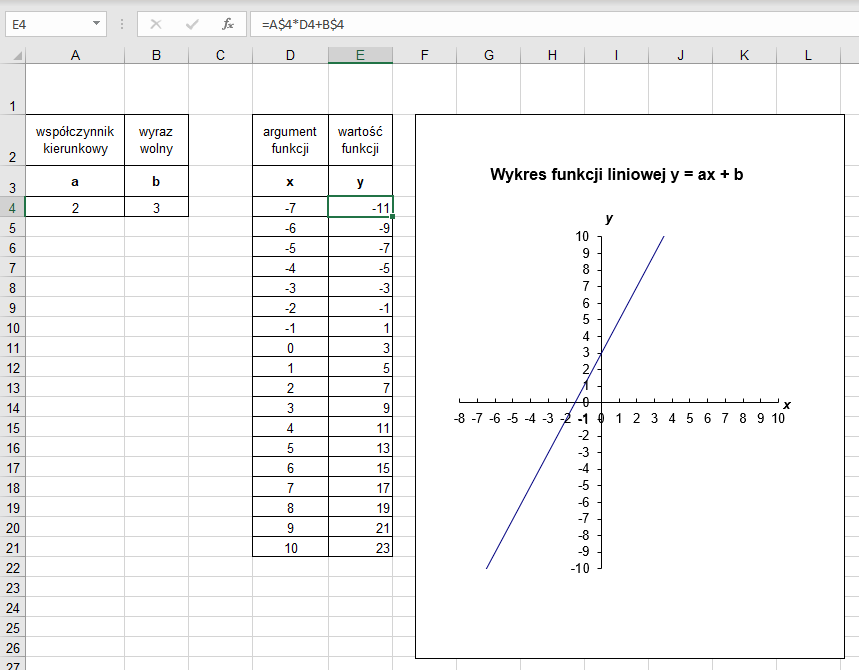
Aby sporządzić wykres funkcji liniowej y = ax + b, należy podać wartość współczynnika kierunkowego i wyrazu wolnego oraz sporządzić tabelę do obliczania wartości funkcji dla podanych argumentów.
Formuła w komórce E4 (rys. 6.) ma postać = A$4*D4+B$4.
![]() Ćwiczenie 10. Tworzymy wykres funkcji liniowej w arkuszu kalkulacyjnym
Ćwiczenie 10. Tworzymy wykres funkcji liniowej w arkuszu kalkulacyjnym
- Korzystając z rysunku 6., przygotuj tabelę do obliczania wartości i utwórz wykres funkcji liniowej: y = ax + b. Wyjaśnij, dlaczego w formule zastosowano adresowanie mieszane.
- Zapisz plik pod nazwą TB2_c10_Funkcja liniowa.
- Przetestuj rozwiązanie, zmieniając wartości współczynnika kierunkowego i wyrazu wolnego. Omów, jakie wartości powinien mieć współczynnik kierunkowy, aby powstały wykresy funkcji rosnącej, malejącej i stałej.
2.2. Wykres wielomianu
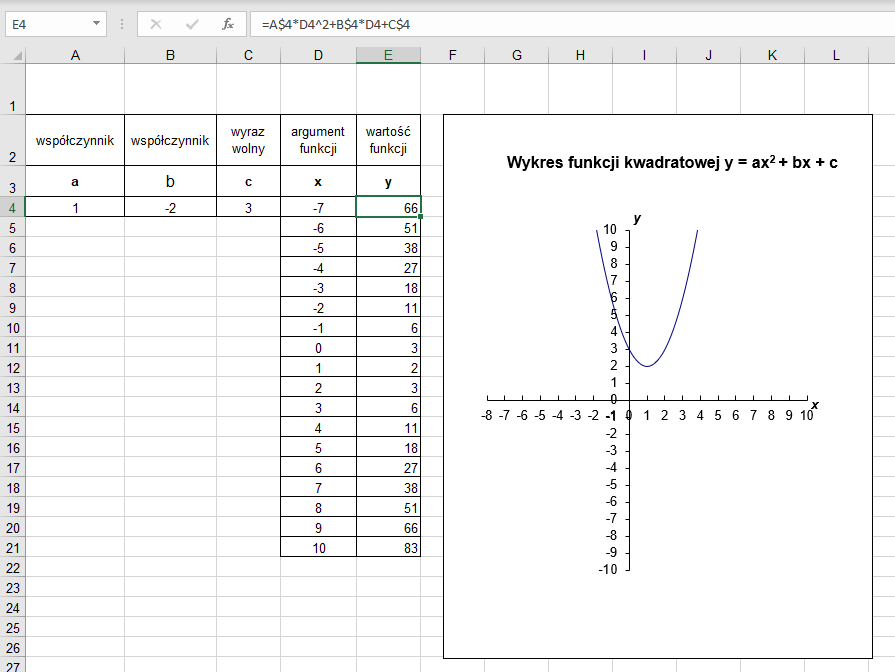
Wykonamy w arkuszu kalkulacyjnym wykres funkcji kwadratowej y = ax2 + bx + c, która jest wielomianem drugiego stopnia. Wykresem funkcji kwadratowej jest parabola, a położenie wykresu względem osi OX zależy od wartości Δ i współczynnika a.
Formuła w komórce E4 (rys. 7.) ma postać: =A$4*D4^2+B$4*D4+C$4.
![]() Ćwiczenie 11. Tworzymy wykres funkcji kwadratowej w arkuszu kalkulacyjnym
Ćwiczenie 11. Tworzymy wykres funkcji kwadratowej w arkuszu kalkulacyjnym
- W arkuszu kalkulacyjnym utwórz wykres funkcji kwadratowej. Sprawdź rozwiązanie dla różnych danych, w tym dla ujemnego współczynnika a. W razie potrzeby zmień zakres danych (wartości argumentów x).
- Zapisz plik pod nazwą TB2_c11_Funkcja kwadratowa.
Wskazówka: Skorzystaj z rozwiązania ćwiczenia 10. Dodaj drugi współczynnik i zmodyfikuj formułę na obliczenie wartości funkcji.
Powtórzenie wiadomości z matematyki:
Współrzędne wierzchołka paraboli (xw, yw) są określane wzorami:
![]()
![]()
![]() Ćwiczenie 12. Modyfikujemy rozwiązanie ćwiczenia 11.
Ćwiczenie 12. Modyfikujemy rozwiązanie ćwiczenia 11.
- W rozwiązaniu ćwiczenia 11. dodaj formuły obliczające wartości pierwiastków równania kwadratowego (temat B1, przykład 3.), czyli wartości argumentów x, dla których funkcja przyjmuje wartość zero. Dodaj również formuły obliczające współrzędne wierzchołka paraboli.
- Zapisz plik pod nazwą TB2_c12_Funkcja kwadratowa.
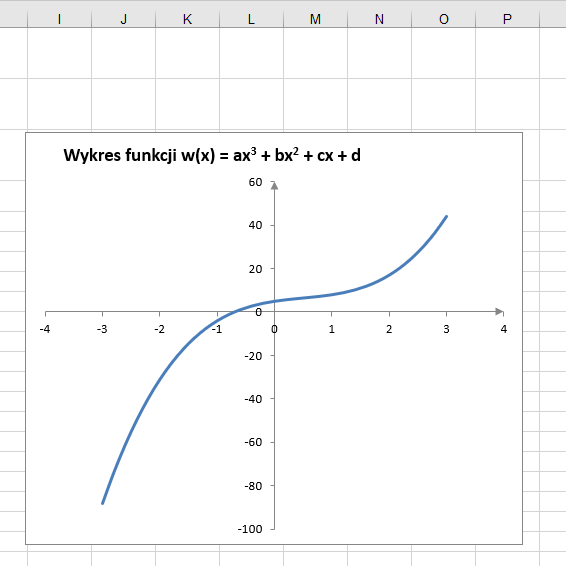
W podobny sposób, jak w przypadku funkcji kwadratowej, można wykonać obliczenia i utworzyć wykres wielomianu trzeciego stopnia: W(x) = ax3 + bx2 + cx + d.
W arkuszu kalkulacyjnym można wykonać wykres dowolnej funkcji. Jest to przydatne, szczególnie gdy zadana funkcja jest opisana skomplikowanym wzorem, dla którego nie znamy gotowych reguł rozwiązań. Trudność może stanowić wyznaczenie przedziału liczbowego, dla którego trzeba przedstawić wykres. Przedział ten powinien być na tyle szeroki, aby można było określić również część funkcji poza nim.
![]() Ćwiczenie 13. Tworzymy wykres wielomianu w arkuszu kalkulacyjnym
Ćwiczenie 13. Tworzymy wykres wielomianu w arkuszu kalkulacyjnym
- Utwórz w arkuszu kalkulacyjnym wykres wielomianu trzeciego stopnia W(x) = ax3 + bx2 + cx + d.
- Zapisz plik pod nazwą TB2_c13_Wielomian.
Wskazówka: Aby wykres był dokładniejszy, ustal zakres argumentów x od -3 do 3 co 0,2 (tak przygotowano wykres przedstawiony na rysunku 8.).
2.3. Wykres funkcji trygonometrycznej
W arkuszu kalkulacyjnym można przedstawić wykres każdej funkcji trygonometrycznej. Służą do tego funkcje: SIN (sinus), COS (cosinus), TAN (tangens).
Aby utworzyć wykres, należy odpowiednio przygotować argumenty – w arkuszu kalkulacyjnym argumenty funkcji trygonometrycznych podaje się w radianach, a nie w stopniach.
![]() Przykład 9. Tworzenie wykresu funkcji tangens w arkuszu kalkulacyjnym
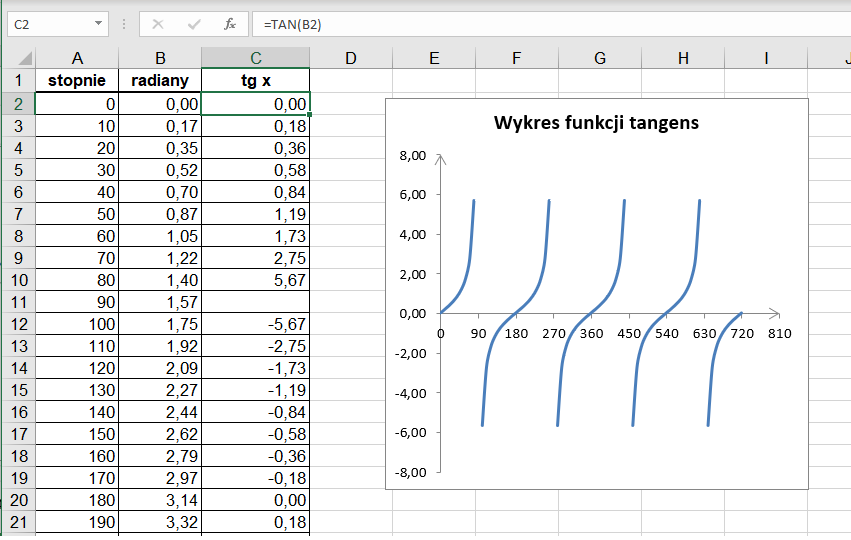
Przykład 9. Tworzenie wykresu funkcji tangens w arkuszu kalkulacyjnym
W kolumnie A (rys. 9.) umieszczamy wartości argumentów w stopniach, np. od 0° do 720° w zadanych odstępach, np. co 10°, które w kolumnie B przeliczamy na radiany.
Formuła w komórce B2 ma postać: =A2 *PI()/180.
W kolumnie C wprowadzamy formułę obliczającą wartości funkcji dla zadanych parametrów: =TAN(B2). Wartości w kolumnach B i C można zaokrąglić, np. do dwóch miejsc po przecinku.
Uwaga: Opisaną metodą można narysować wykres każdej funkcji trygonometrycznej, odpowiednio zmieniając formułę z kolumny C i dostosowując wartości argumentów w kolumnie A. Nie wszystkie funkcje trygonometryczne są określone w całym zbiorze liczb rzeczywistych, np. funkcja tangens nie jest określona dla …-90°, 90°, 270°…, czyli nieparzystych wielokrotności kąta 90°. Dlatego komórkę, w której powinna być umieszczona formuła, pozostawiamy niewypełnioną.
![]() Ćwiczenie 14. Tworzymy wykres funkcji tangens w arkuszu kalkulacyjnym
Ćwiczenie 14. Tworzymy wykres funkcji tangens w arkuszu kalkulacyjnym
- Wykonaj w arkuszu kalkulacyjnym wykres funkcji: f(x) = tg x (w przedziale od 0° do 720°).
- Zapisz plik pod nazwą TB2_c14_Funkcja tangens.
2.4. Wykres funkcji logarytmicznej
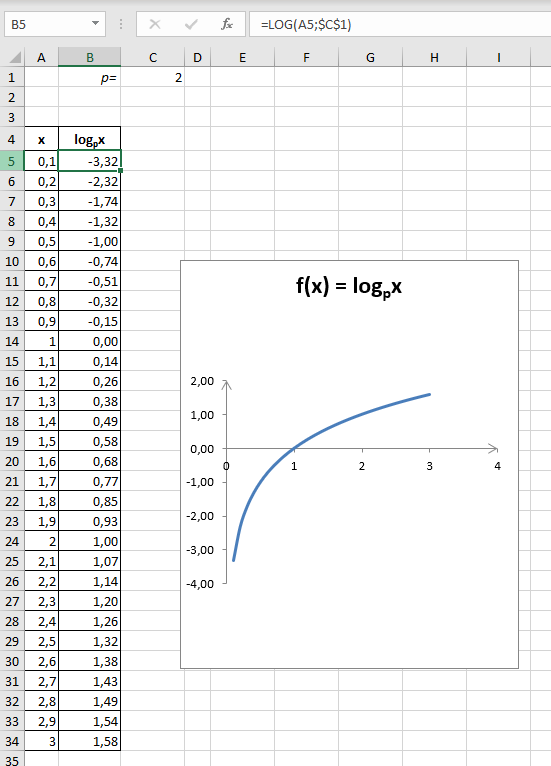
Korzystając z funkcji arkusza LOG, możemy narysować wykres funkcji logarytmicznej o podstawie większej od 0 i różnej od 1 oraz liczbie logarytmowanej większej od 0.
Na rysunku 14. pokazano wykres funkcji logarytmicznej o podstawie 2: f(x) = log2x.
Formuła w komórce B2 ma postać: =LOG(A2;2).
Powtórzenie wiadomości z matematyki:
Funkcja logarytmiczna
f(x) = logax, gdzie:
x – liczba logarytmowana (argument funkcji), x > 0;
a – podstawa logarytmu, a > 0 i a ≠ 1;
f(x) – logarytm (wartość funkcji).
![]() Ćwiczenie 15. Tworzymy wykres funkcji logarytmicznej w arkuszu kalkulacyjnym
Ćwiczenie 15. Tworzymy wykres funkcji logarytmicznej w arkuszu kalkulacyjnym
- Wykonaj w arkuszu kalkulacyjnym wykres funkcji logarytmicznej: f(x) = logpx dla argumentów x z przedziału od 1 do 3 (co 0,2). Wartość podstawy p umieść w komórce C1, a adres tej komórki – w formule na obliczenie logarytmu. Wyjaśnij, jaki rodzaj adresowania należy zastosować dla komórki C1.
- Zapisz plik pod nazwą TB2_c15_Funkcja tangens.
 Zadania
Zadania
- Otwórz plik TB2_z1_Ubezpieczenia.xls i wykonaj obliczenia zgodnie z poleceniami podanymi pod tabelą.
Wskazówki: Należy zauważyć, że imiona żeńskie podane w zadaniu kończą się literą „a”. Aby automatycznie określić płeć poszczególnych osób, można skorzystać z funkcji tekstowej PRAWY. Jeśli jako test logiczny w funkcji JEŻELI wykorzystamy funkcję PRAWY, sprawdzającą, czy ostatnią literą imienia danej osoby jest „a”, to możemy użyć tej funkcji do wygenerowania napisów określających płeć poszczególnych osób w kolumnie D (K – kobieta, M – mężczyzna).
Do obliczenia sumy miesięcznych składek dla kobiet oraz sumy miesięcznych składek dla mężczyzn należy użyć funkcji SUMA.JEŻELI. - Korzystając z arkusza kalkulacyjnego, oblicz:
a. na ile sposobów trzech uczniów może zająć miejsca na sali, na której są 42 krzesła (uczniowie są nierozróżnialni.)
b. na ile sposobów można wybrać dokładnie trzy śruby dobre i dwie złe z pudełka zawierającego 100 śrub, z których 10% to śruby wadliwe. - Przygotuj arkusz, w którym będzie można utworzyć wykres funkcji liniowej y = -2x – 4,5.
- Zmodyfikuj formułę utworzoną w ćwiczeniu 13., zmieniając postać klasyczną wielomianu na postać zgodną ze schematem Hornera (zob. Materiał edukacyjny, część 1., temat C9).
- Utwórz w arkuszu kalkulacyjnym wykres funkcji cotangens.
Wskazówka: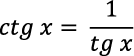 .
. - Utwórz w arkuszu kalkulacyjnym wykres funkcji:
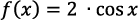 .
. - Utwórz w arkuszu kalkulacyjnym wykres funkcji:
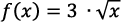 .
.

