Algorytmy sortowania

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1) wyróżnia w problemie podproblemy i charakteryzuje: metodę połowienia, stosuje podejście zachłanne i rekurencję;
2) porównuje działanie różnych algorytmów dla wybranego problemu, analizuje algorytmy na podstawie ich gotowych implementacji;
3) w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
4) do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
2) sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;
I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1) zapisuje za pomocą listy kroków lub pseudokodu i implementuje w wybranym języku programowania algorytmy poznane na wcześniejszych etapach oraz algorytmy:
     e) sortowania ciągu liczb przez scalanie,
3) objaśnia, a także porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przy tym przykłady problemów i algorytmów, w szczególności:
     a) wyszukiwanie elementów liniowe i przez połowienie (do znajdowania elementów w zbiorze, sortowania przez wstawianie, przybliżonego rozwiązywania równań),
     b) rekurencję (do generowania ciągów liczb, potęgowania, sortowania liczb, generowania fraktali),
     c) metodę dziel i zwyciężaj (jednoczesne znajdowanie minimum i maksimum, sortowanie przez scalanie i szybkie)

Spis treści

1. Sortowanie przez scalanie – stosowanie iteracji, metody dziel i zwyciężaj i rekurencji
2. Sortowanie przez wstawianie metodą wyszukiwania liniowego
3. Sortowanie szybkie – stosowanie metody dziel i zwyciężaj i rekurencji

1. Sortowanie przez scalanie – stosowanie iteracji, metody dziel i zwyciężaj i rekurencji

Mamy dwa ciągi liczb:

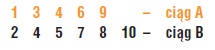
Scalając je w jeden (z zachowaniem rosnącego porządku liczb), otrzymamy:

Przykład 1. Łączenie (scalanie) dwóch ciągów uporządkowanych rosnąco w jeden ciąg uporządkowany rosnąco – algorytm iteracyjny

Zadanie: Połącz dwa uporządkowane ciągi elementów w jeden uporządkowany ciąg, stosując iteracyjny algorytm sortowania przez scalanie.
Dane: uporządkowane rosnąco ciągi elementów A i B.
Wynik: ciąg AB zawierający uporządkowane rosnąco elementy ciągów A i B.

Lista kroków:

1. Zacznij algorytm.
2. Jeśli w ciągu A lub B nie ma elementów, przejdź do kroku 5.
3. Porównaj wartość pierwszego elementu ciągu A z pierwszym elementem ciągu B. Dodaj mniejszy z elementów do ciągu AB i usuń go z ciągu, z którego został pobrany. Jeśli elementy są równe, dodaj je kolejno do ciągu AB i usuń z ciągów A i B.
4. Przejdź do kroku 2.
5. Jeśli w ciągu A zostały elementy, to dopisz je na koniec ciągu AB.
6. Jeśli w ciągu B zostały elementy, to dopisz je na koniec ciągu AB.
7. Zakończ algorytm.

Ćwiczenie 1. Analizujemy algorytm scalania uporządkowanych ciągów

1. Przeanalizuj algorytm scalania uporządkowanych ciągów, wykonując go dla ciągów A (2, 5, 12, 18, 90, 112, 300) i B (1, 8, 12, 49, 92, 100).
2. Podaj liczbę porównań elementów wykonanych przy scalaniu tych ciągów.

Przykład 2. Programowanie algorytmu sortowania przez scalanie – iteracyjny algorytm scalania uporządkowanych ciągów

W programie w języku C++ zdefiniujemy strukturę Dane do pamiętania danych. Typ Dane określa właśnie typ funkcji wprowdzDane(), która służy do wprowadzania liczb (elementów ciągu z klawiatury) i jest dwukrotnie wywoływana w programie głównym.

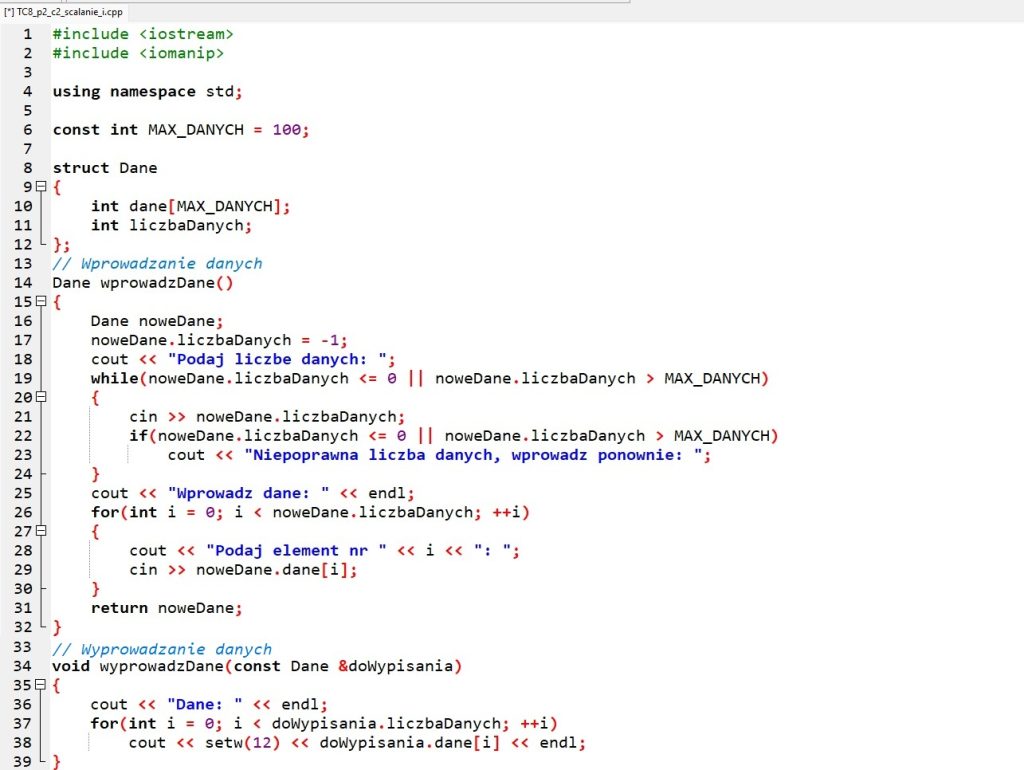
Do scalania danych zdefiniujemy funkcję scalPosortowaneCiagi().

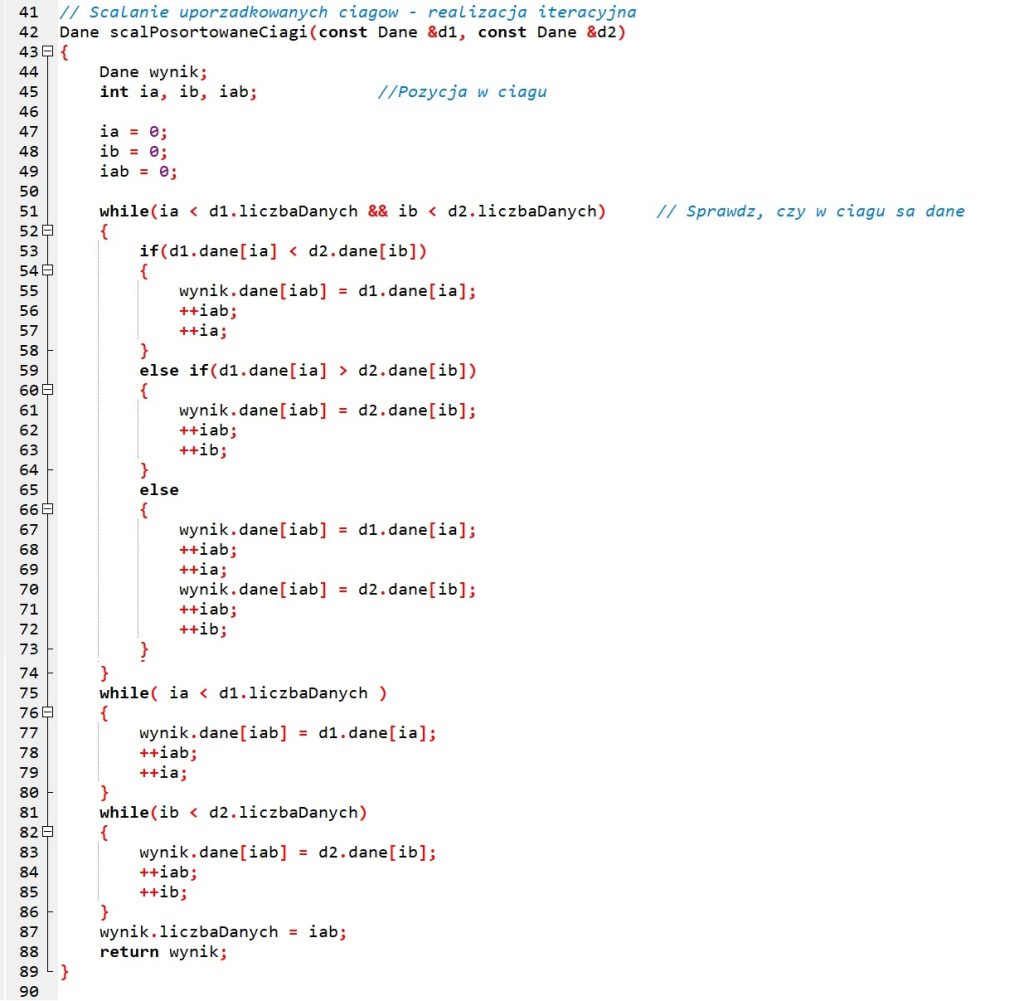
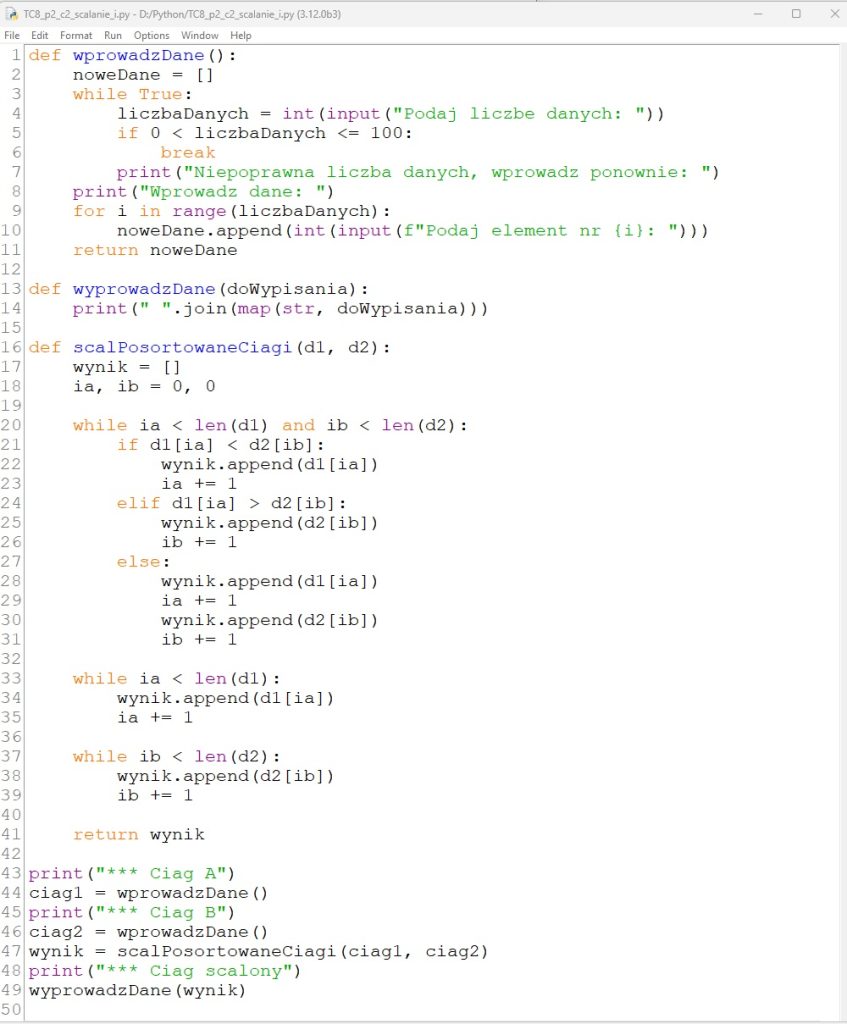
W języku Python nie ma potrzeby tworzenie dodatkowej struktury na dane. Będziemy przekazywali listy elementów, a ich długość będziemy sprawdzali wbudowaną funkcją len().

Do scalania danych zdefiniujemy funkcję scalPosortowaneCiagi().

W funkcji wykorzystamy metodę append(), która umożliwia wstawianie nowego elementu do listy. Elementy są dołączane po prawej stronie istniejącej listy. Metoda append() zwiększa rozmiar listy o 1. Na przykład w wierszu 22: instrukcja wynik.append(d1[ia]) dodaje jeden element do listy wynik[].

Ćwiczenie 2. Analizujemy program realizujący iteracyjny algorytm scalania uporządkowanych ciągów

1. Otwórz plik TC8_p2_c2_scalanie_i.cpp lub TC8_p2_c2_scalanie_i.py.
2. Przeanalizuj fragmenty kodu programu, korzystając z przykładu 2. Objaśnij działanie funkcji. Uruchom program i wykonaj go kilkakrotnie dla różnych danych.

Przykład 3. Sortowanie ciągu liczb przez scalanie – zastosowanie metody dziel i zwyciężaj i rekurencji

Zadanie: Posortuj ciąg elementów, wykorzystując metodę dziel i zwyciężaj i rekurencję.
Dane: ciąg elementów A, indeks pierwszego elementu w ciągu: pierwszy, indeks ostatniego elementu w ciągu: ostatni.
Wynik: uporządkowany rosnąco ciąg A.

Lista kroków:

1. Zacznij algorytm.
2. Jeśli pierwszy < ostatni, to oblicz: srodek = (pierwszy + ostatni) %2;
   w przeciwnym wypadku przejdź do kroku 6.
3. Zapisz jako ciąg X wynik działania algorytmu dla danych: (ciąg A, pierwszy, srodek).
4. Zapisz jako ciąg Y wynik działania algorytmu dla danych: (ciąg A, srodek+ 1, ostatni).
5. Zwróć jako wynik działania algorytmu ciągi X i Y scalone w jeden uporządkowany ciąg.
6. Zakończ algorytm.

% – operator obliczania reszty dzielenia dwóch liczb całkowitych w językach C++ i Python

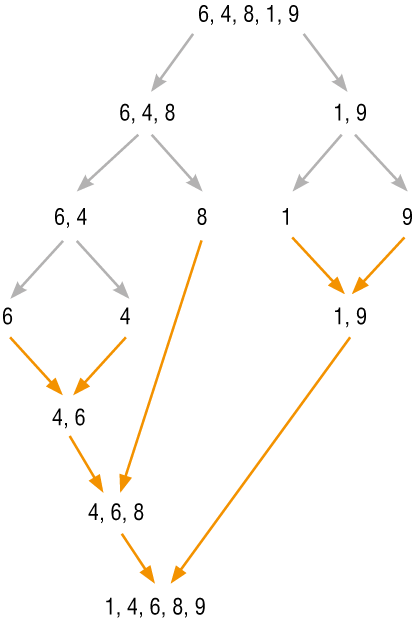
Uwaga: Na rysunku 1. zilustrowano ten algorytm dla ciągu (6, 4, 8, 1, 9). Szare strzałki symbolizują dokonywane podziały, a pomarańczowe – operacje scalania w ciągi uporządkowane.

Ćwiczenie 3. Analizujemy algorytm sortowania przez scalanie

Przeanalizuj algorytm sortowania przez scalanie, korzystając z rysunku 1. Wykonaj algorytm dla liczb (2, 5, 1, 8, 0, 11, 3), tworząc podobny rysunek.

Przykład 4. Programowanie algorytmu sortowania przez scalanie – zastosowanie metody dziel i zwyciężaj i rekurencji

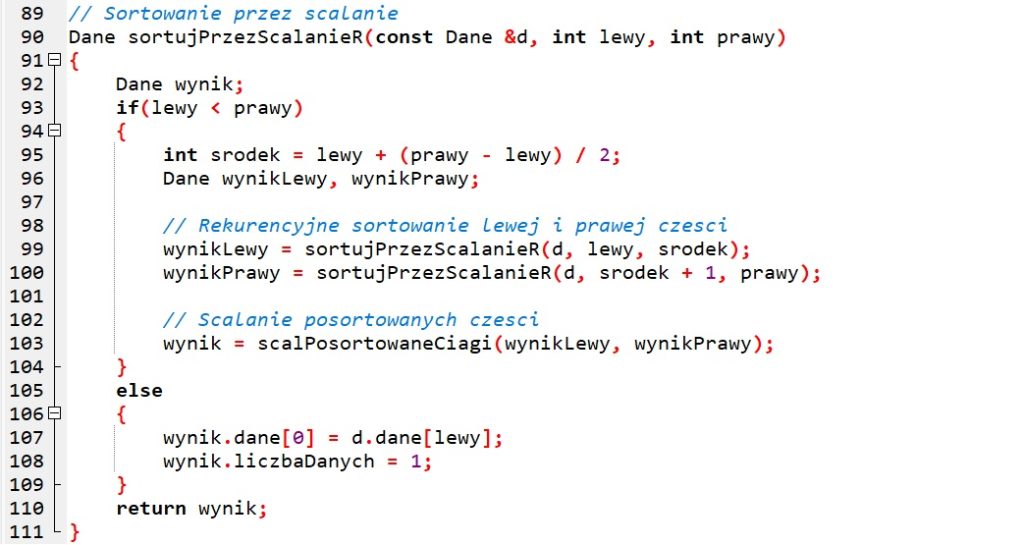
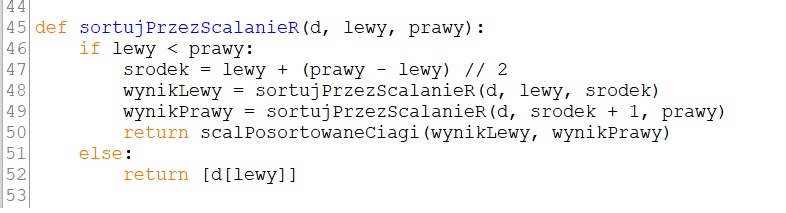
W programie zapisanym w pliku TC8_p4_c4_scalanie_i+r.cpp lub TC8_p4_c4_scalanie_i+r.py korzystamy z programu realizującego iteracyjny algorytm scalania uporządkowanych ciągów (pliki TC8_p2_c2_scalanie_i.cpp lub TC8_p2_c2_scalanie_i.py), w którym zdefiniowano funkcje wprowadzania danych wprowadzDane() i ich wyprowadzania wyprowadzDane() oraz scalania iteracyjną funkcję scalania dwóch uporządkowanych ciągów scalPosortowaneCiagi(). Do programu dodaliśmy rekurencyjną funkcję sortujPrzezScalanieR() w której dzielimy wprowadzony ciąg liczb na dwa podciągi uporządkowane zgodnie z listą kroków podaną w przykładzie 3. i pokazaną na rysunku 1 (wiersze 99 i 100 programu w C++ lub 48 i 49 w Pythonie). Następnie (w wierszu 103 w C++ lub w wierszu 50 w Pyhonie) wywołujemy funkcję scalPosortowaneCiagi(), która umożliwi scalenie otrzymanych dwóch uporządkowane ciągów.

Ćwiczenie 4. Analizujemy program realizujący algorytm sortowania prze scalanie

1. Otwórz plik TC8_p4_c4_scalanie_i+r.cpp lub TC8_p4_c4_scalanie_i+r.py. Uruchom program.
2. Objaśnij działanie funkcji sortujPrzezScalanieR, korzystając z przykładu 4. Porównaj implementację z graficzną wizualizacją z rysunku1. Wskaż miejsce wywołania rekurencyjnego funkcji sortujPrzezScalanieR(). Omów zastosowane struktury danych

1. Sortowanie przez wstawianie metodą wyszukiwania liniowego

Metodę sortowania (porządkowania) przez wstawianie (inaczej przez umieszczanie) stosujemy często w życiu codziennym – na przykład gdy w bibliotece odkładamy książkę na półkę, znajdujemy odpowiednie miejsce, patrząc na nazwiska autorów książek umieszczonych na półce.

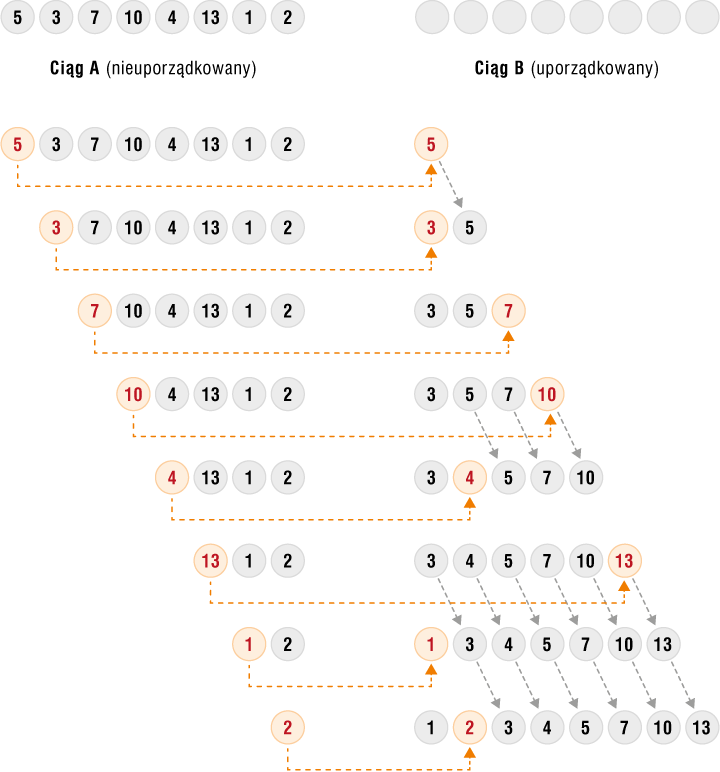
Aby znaleźć miejsce umieszczenia nowego elementu w ciągu uporządkowanym, zastosujemy metodę liniową, w której porównuje się wstawiany element z kolejnymi elementami ciągu uporządkowanego. Na rysunku 2. pokazano przykład porządkowania liczb rosnąco.

Przykład 5. Sortowanie ciągu elementów liniową metodą wstawiania (algorytm iteracyjny)

Zadanie: Posortuj ciąg elementów liniową metodą wstawiania, stosując algorytm iteracyjny.
Dane: Niepusty ciąg elementów A.
Wynik: Ciąg B, zawierający wszystkie elementy ciągu A uporządkowane w kolejności rosnącej.

Lista kroków:

1. Zacznij algorytm.
2. Przenieś pierwszy element ciągu A do ciągu B.
3. Jeśli w ciągu A nie ma elementów, przejdź do kroku 7.
4. Porównuj element początkowy z kolejnymi elementami ciągu B i umieść go przed pierwszym elementem, który będzie większy od niego lub równy. Jeśli w ciągu B nie ma takiego elementu, umieść element początkowy na końcu ciągu B.
5. Usuń element początkowy z ciągu A.
6. Przejdź do kroku 3.
7. Zakończ algorytm.

Ćwiczenie 5. Analizujemy algorytm sortowania przez wstawianie

1. Przeanalizuj algorytm porządkowania przez wstawianie, wykonując go dla ciągu liczb (3, 4, 10, 7, 1, 5, 2, 8). Podaj liczbę porównań wykonanych w celu uporządkowania tego ciągu.
2. Wykonaj podobne praktyczne ćwiczenie, porządkując inny ciąg liczb. Podaj liczbę porównań wykonanych w celu uporządkowania tego ciągu.
   Wskazówka: Przygotuj niezbędne pomoce dydaktyczne, np. kartoniki z zapisanymi liczbami.

Przykład 6. Programowanie algorytmu sortowania przez wstawianie w językach C++ i Python – wersja iteracyjna

Zdefiniujemy funkcję sort_wstaw() do sortowania danych, a w niej zdefiniujemy dodatkową tablicę (listę) b[N], w której wstawiamy na odpowiednich miejscach elementy z tablicy (listy) a[N]. Tablica (lista) b[N] na początku jest pusta (nie zawiera żadnych elementów).

Przyjęliśmy następujące oznaczenia dla zmiennych:
– akt – aktualnie sprawdzany element tablicy (listy) a[N],
– indeks_b – indeks elementu tablicy (listy) b[N], który określa miejsce wstawienia aktualnego elementu tablicy (listy) a[N],
– licz_posort – liczba posortowanych elementów w tablicy (liście) b[N].

Ćwiczenie 6. Zapisujemy algorytm porządkowania przez wstawianie w językach C++ lub Python

1. Otwórz plik TC8_p6_c6_wstawianie_i.cpp lub TC8_p6_c6_wstawianie_i.py. Przeanalizuj kod funkcji i wskaż, który fragment programu odpowiada za znalezienie punktu wstawienia.
2. Wykorzystując funkcję sort_wstaw(), napisz program sortujący rosnąco metodą przez wstawianie liczby wprowadzone do dziesięcioelementowej tablicy (listy).
   1. Uzupełnij program o definicje funkcji wprowadzania z klawiatury elementów do tablicy (listy) i do ich wyprowadzenia na ekran: odpowiednio funkcje wprowadz_dane() i wyprowadz_dane(),
   2. wszystkie funkcje wywołaj w programie głównym, przy czym funkcję wyprowadz_dane() dwukrotnie – wyświetlaj dane przed uporządkowaniem i po uporządkowaniu.
3. Zapisz plik pod tą samą nazwą.
4. Uruchom i przetestuj kilkakrotnie program dla różnych danych.

3. Sortowanie szybkie – stosowanie metody dziel i zwyciężaj i rekurencji

Algorytm sortowania metodą szybką (QuickSort) jest jednym z najszybszych stosowanych obecnie algorytmów sortowania, biorąc pod uwagę średni czas wykonania obliczeń dla różnych zbiorów danych. Jest jednocześnie jednym z najczęściej wykorzystywanych algorytmów – zaimplementowano go w standardowych bibliotekach popularnych języków programowania.

Mechanizm postępowania w algorytmie sortowania metodą szybką jest następujący:

1. Wybieramy element ciągu v (najczęściej pierwszy element ciągu lub leżący pośrodku), tzw. pivot.
2. Dzielimy ciąg na dwa podciągi: w lewym znajdują się elementy nie większe niż wybrany element v, a w prawym – nie mniejsze niż v.
3. Po wykonaniu tego kroku, element v możemy umieścić między tymi podciągami, gdyż jest to właściwe dla niego miejsce w szukanym, uporządkowanym ciągu.
4. Dopóki długość każdego z podciągów (lewego i prawego) jest większa od 1, wywołujemy dla każdego z nich tę samą procedurę sortującą.

Dla poprawności działania algorytmu sortowania metodą szybką nie ma znaczenia, który element zostanie wybrany do rozdzielenia ciągu wejściowego. Często jednak, w celu zoptymalizowania działania algorytmu, wybiera się element środkowy.

Przykład 7. Określenie zadania i jego specyfikacji oraz pseudokod algorytmu sortowania metodą szybką

Zadanie: Posortuj elementy tablicy (listy) metodą szybką.
Dane: tablica (lista) n liczb całkowitych.
Wynik: liczby w tablicy (w liście) posortowane niemalejąco.

Pseudokod algorytmu

W pseudokodzie uwzględniono przypadek, gdy wybranym elementem (nazwanym pivot) jest element środkowy.

funkcja quick_sort(array, p, k)
     i ⇽ p      # p – indeks początku tablicy (listy)
     j ⇽ k      # k – indeks końca tablicy
     pivot ⇽ array[(p + k) div 2]
   dopóki i ≤ j wykonuj
     dopóki array[i] < pivot wykonuj i ⇽ i + 1
     dopóki array[j] > pivot wykonuj j ⇽ j - 1
     jeśli i ≤ j to
         Zamień(array[i], array[j])
         i ⇽ i + 1
         j ⇽ j - 1
     jeśli p < j to quick_sort(array, p, j)
     jeśli i < k to quick_sort(array, i, k)


Ćwiczenie 7. Analizujemy rekurencyjny algorytm sortowania metodą szybką

Przeanalizuj rekurencyjny algorytm porządkowania metodą szybką, wykonując go dla liczb (2, 5, 12, 18, 9, 11, 20, 82). Podaj liczbę porównań elementów, wykonanych w celu uporządkowania tego ciągu.

Przykład 8. Programowanie algorytmu sortowania szybkiego w językach C++ i Python – wersja rekurencyjna

Ćwiczenie 8. Programujemy rekurencyjny algorytm sortowania metodą szybką

1. Otwórz plik TC8_p8_c8_szybki_r.cpp lub TC8_p8_c8_szybki_r.py.
2. Wykorzystując rekurencyjną funkcję szybkiego sortowania quicksort(), napisz program sortujący losowo wygenerowaną tablicę (listę) n – elementów.
3. Zapisz plik pod tą samą nazwą.

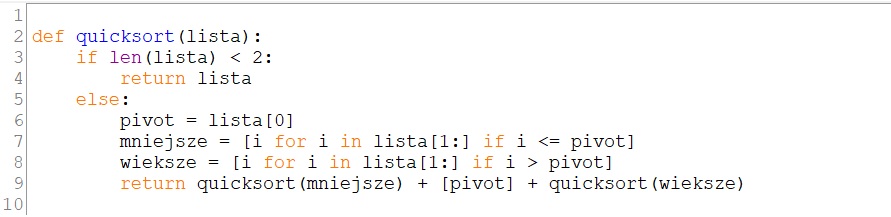
Przykład 9. Wykorzystanie list składanych w języku Python do programowania algorytmu sortowania szybkiego

W języku Python, wykorzystując listy składane, możemy znacznie uprościć kod źródłowy szybkiego sortowania. Argumentem funkcji jest wtedy tylko lista, bez indeksów jej początku i końca. Poniżej przykładowy kod funkcji, w której elementem osiowym (pivotem) jest pierwszy element listy. Może nim być element środkowy lub ostatni.

Zadania

TC8_p2_c2_scalanie_i.cppPobierz
TC8_p2_c2_scalanie_i.pyPobierz
1. Otwórz plik TC8_p2_c2_scalanie_i.cpp lub TC8_p2_c2_scalanie_i.py. Zmodyfikuj program tak, aby sortował n liczb wygenerowanych losowo i zapisanych w tablicy (liście). Zapisz program w pliku pod nazwą TC8_p2_scalanie_los.cpp lub TC8_p2_scalanie_los.py.
TC8_p8_c8_szybki_r.cppPobierz
TC8_p8_c8_szybki_r.pyPobierz
2. Otwórz plik TC8_p8_c8_szybki_r.cpp lub TC8_p8_c8_szybki_r.py. Zmodyfikuj program tak, aby posortował liczby malejąco. Zapisz program w pliku pod nazwą TC8_p8_c8_szybki_r_malejacy.cpp lub TC8_p8_c8_szybki_r_malejacy.py
Dla zainteresowanych
TC8_p8_c8_szybki_r.pyPobierz
3. Otwórz plik TC8_p8_c8_szybki_r.py. Zmodyfikuj program, sprawdzając działanie funkcji pokazanej w przykładzie 9. Zapisz program w pliku pod nazwą TC8_p9_z3_szybki_r.py