Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.
Zapisy podstawy programowej 2024 realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
- do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- projektuje i tworzy programy w procesie rozwiązywania problemów, wykorzystuje w programach dobrane do algorytmów struktury danych, w tym struktury dynamiczne i korzysta z dostępnych bibliotek dla tych struktur;
- sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;
- wykorzystuje znane sobie algorytmy przy rozwiązywaniu i programowaniu rozwiązań następujących problemów:
c) znajdowania w ciągu podciągów o różnorodnych własnościach, np. najdłuższego spójnego podciągu niemalejącego, spójnego podciągu o największej sumie,
Spis treści
- Podciąg, spójny podciąg i spójny podciąg niemalejący
- Znajdowanie najdłuższego spójnego podciągu niemalejącego
- Znajdowanie spójnego podciągu o największej sumie
1. Podciąg, spójny podciąg i spójny podciąg niemalejący
![]() Przykład 1. Przykłady podciągów
Przykład 1. Przykłady podciągów
Dany jest ciąg: (23, 6, 7, 9, 11, 5, 90, 1, 35, 100).
Liczby: 7, 9, 1 i 100 tworzą podciąg danego ciągu.
Liczby 5, 90, 1, 35 tworzą tzw. spójny podciąg.
Liczby 6, 7, 9, 11; 5, 90; 1, 35, 100 tworzą podciągi spójne niemalejące.
Liczby 6, 7, 9, 11 tworzą najdłuższy podciąg spójny niemalejący.
![]() Ćwiczenie 1. Podajemy przykłady podciągów spójnych
Ćwiczenie 1. Podajemy przykłady podciągów spójnych
- Odpowiedz na pytania:
- Czy liczby 90, 6, 5, 23 tworzą podciąg ciągu podanego w przykładzie 1?
- Czy liczby 6, 7, 9, 5 tworzą podciąg spójny?
- Podaj przykłady podciągów, podciągów spójnych i podciągów spójnych niemalejących, inne niż podane w przykładzie 1.
Gdy elementy podciągu spójnego uporządkowane są malejąco, mówimy o podciągu spójnym malejącym. Gdy elementy podciągu spójnego uporządkowane są rosnąco, mówimy o podciągu spójnym rosnącym.
Gdy każdy kolejny element podciągu spójnego jest mniejszy od poprzedniego lub jest mu równy, mówimy o podciągu spójnym nierosnącym. Gdy każdy kolejny element podciągu spójnego jest większy od poprzedniego lub jest mu równy, mówimy o podciągu spójnym niemalejącym.
Podciągi można tworzyć również z ciągów składających się z liter lub nawet tekstów. Dla podciągów rosnących, malejących, nierosnących, niemalejących i stałych ważne jest, aby dla każdych dwóch elementów ciągu istniała relacja porządkująca, pozwalająca na określenie, który z elementów jest większy lub czy są one sobie równe. W tym temacie wymagane algorytmy omówimy jednak na przykładzie ciągów liczbowych.
Warto zauważyć, że podciąg składający się z jednego elementu zawsze będzie spójny.
2. Znajdowanie najdłuższego spójnego podciągu niemalejącego
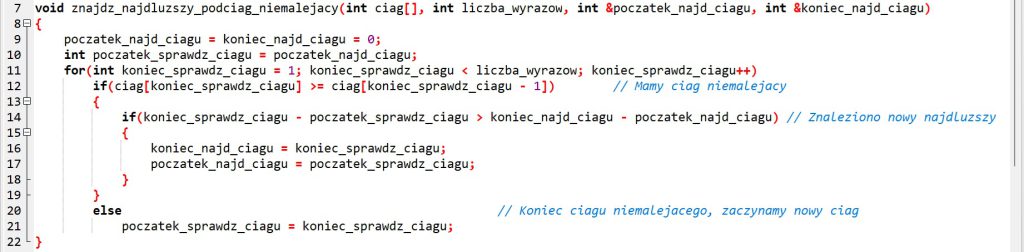
Zdefiniujemy funkcję znajdz_najdluzszy_podciag_niemalejacy() znajdującą najdłuższy spójny podciąg niemalejący (dalej: NSPNm) w tablicy lub liście liczb ciag[] przekazanej jako parametr funkcji (dodatkowo jako kolejny parametr funkcji przekazać musimy liczbę elementów tablicy lub listy). Wynikiem działania funkcji będzie para liczb określających indeksy pierwszego i ostatniego elementu NSPNm (alternatywnie wynikiem może być np. indeks pierwszego elementu podciągu i długość podciągu). Ponieważ w języku C++ funkcja nie może zwrócić dwóch liczb, zastosujemy przekazywanie parametrów przez referencję (w języku C++ przed nazwą parametru umieszcza się znak & i przy wywołaniu funkcji parametrem aktualnym musi być zmienna, nie może być wyrażenie) – po zakończeniu funkcji parametry początek_najd_ciagu i koniec_najd_ciagu zawierać będą indeksy odpowiedniego pierwszego i ostatniego elementu NSPNm.
W algorytmie wykorzystamy zmienne pomocnicze początek_sprawdz_ciagu i koniec_sprawdz_ciagu, w których pamiętać będziemy odpowiednio początek i koniec aktualnie sprawdzanego niemalejącego podciągu spójnego.
Algorytm zaczynamy od nadania zmiennym wartości początkowych – przyjmujemy, że najdłuższy spójny podciąg składa się z jednego elementu o indeksie 0. Następnie w pętli przeglądamy wszystkie elementy ciągu począwszy od elementu drugiego (o indeksie 1). Jeżeli dany element jest większy lub równy poprzedniemu elementowi, to mamy podciąg niemalejący. W takiej sytuacji sprawdzamy również, czy nowy podciąg jest dłuższy od poprzedniego najdłuższego i jeżeli tak, odpowiednio ustalamy wartości parametrów początek_najd_ciagu i koniec_najd_ciagu.
Jeżeli kolejny element będzie mniejszy od poprzedniego, to mamy koniec podciągu niemalejącego i resetujemy wartość zmiennej początek_sprawdz_ciagu.
![]() Przykład 2. Definicja funkcji znajdowania najdłuższego spójnego podciągu niemalejącego w językach C++ i Python
Przykład 2. Definicja funkcji znajdowania najdłuższego spójnego podciągu niemalejącego w językach C++ i Python



![]() Ćwiczenie 2. Piszemy program znajdujący najdłuższy spójnego podciąg niemalejący
Ćwiczenie 2. Piszemy program znajdujący najdłuższy spójnego podciąg niemalejący
- Otwórz plik TC4_p2_c2.cpp lub TC4_p2_c2.py. Zapoznaj się z pełnym kodem programu. Objaśnij działanie programu, w tym funkcji pokazanej w przykładzie 2.
- Uruchom program kilka razy. Jaki będzie wynik działania programu, jeżeli w danej tablicy (lub liście) znajduje się kilka spójnych podciągów niemalejących o tej samej długości – który z nich zostanie wskazany jako wynik działania programu?
![]() Ćwiczenie 3. Modyfikujemy program znajdujący najdłuższy spójnego podciąg niemalejący
Ćwiczenie 3. Modyfikujemy program znajdujący najdłuższy spójnego podciąg niemalejący
- Otwórz plik TC4_p2_c2.cpp lub TC4_p2_c2.py. Zmodyfikuj program tak, by znajdował najdłuższy spójny podciąg nierosnący.
- Zapisz program w pliku pod nazwą TC4_p2_c3.cpp lub TC4_p2_c3.py.
3. Znajdowanie spójnego podciągu o największej sumie
Aby znaleźć spójny podciąg o największej sumie, możemy:
- poszukać spójnego podciągu np. niemalejącego o największej sumie
lub - poszukać spójnego podciągu o zadanej długości o największej sumie.
W dalszej części tematu zajmiemy się pierwszym przypadkiem, a przypadek pierwszy pozostawiamy uczniom do samodzielnego rozwiązania (zadanie 5. na końcu tematu).
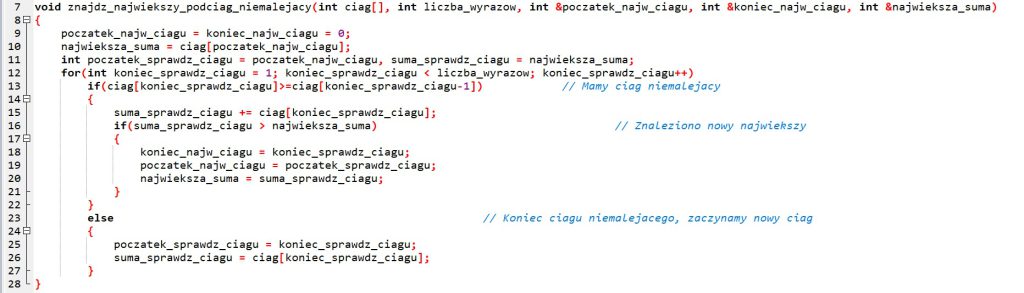
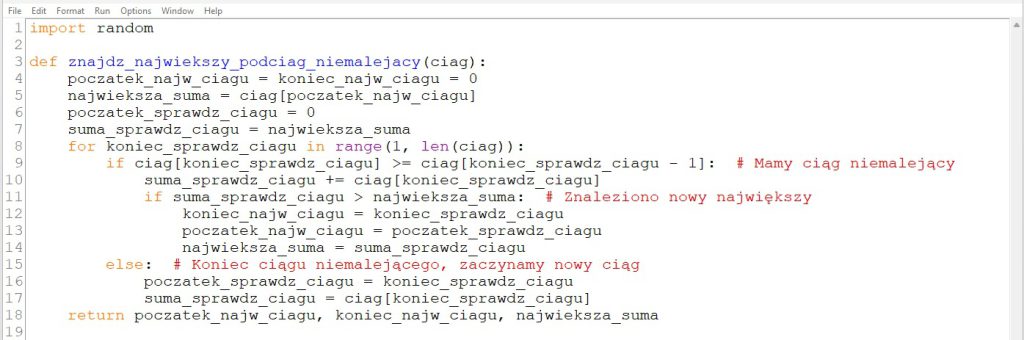
Zdefiniujemy funkcję znajdz_najwiekszy_podciag_niemalejacy() znajdującą spójny podciąg niemalejący o najwyższej sumie w tablicy liczb ciag[] przekazanej jako parametr funkcji (dodatkowo jako kolejny parametr funkcji przekazać musimy liczbę elementów tablicy). Wynikiem działania funkcji będzie para liczb określających indeksy pierwszego i ostatniego elementu spójnego podciągu niemalejącego oraz suma wszystkich elementów podciągu. Podobnie jak w przypadku funkcji znajdz_najdluzszy_podciag_niemalejacy() skorzystamy z przekazywania parametrów przez referencję. Po zakończeniu działania funkcji parametry początek_najw_ciagu i koniec_najw_ciagu zawierać będą indeksy odpowiedniego pierwszego i ostatniego elementu spójnego podciągu niemalejącego, a parametr najwieksza_suma – sumę elementów tego podciagu.
W algorytmie wykorzystamy zmienne pomocnicze początek_sprawdz_ciagu i koniec_sprawdz_ciagu, w których pamiętać będziemy odpowiednio początek i koniec aktualnie sprawdzanego niemalejącego podciągu spójnego oraz suma_sprawdz_ciagu, w której pamiętać będziemy sumę elementów aktualnie sprawdzanego podciągu.
Algorytm zaczynamy od nadania zmiennym wartości początkowych – przyjmujemy, że najdłuższy spójny podciąg składa się z jednego elementu o indeksie 0 i sumie będącej wartością tego elementu. Następnie przeglądamy wszystkie elementy ciągu począwszy od elementu drugiego (o indeksie 1). Jeżeli dany element jest większy lub równy poprzedniemu elementowi, to mamy podciąg niemalejący i zwiększamy wartość sumy o wartość danego elementu. W takiej sytuacji sprawdzamy również, czy suma nowego podciągu jest większa niż aktualnie największa suma i jeżeli tak, odpowiednio ustalamy wartości parametrów początek_najw_ciagu, koniec_najw_ciagu i najwieksza_suma.
Jeżeli kolejny element będzie mniejszy od poprzedniego, to mamy koniec ciągu niemalejącego i resetujemy wartości zmiennych początek_sprawdz_ciagu i suma_sprawdz_ciagu.
![]() Przykład 3. Zapisanie algorytmu znajdowania spójny podciąg o największej sumie w językach C++ i Python
Przykład 3. Zapisanie algorytmu znajdowania spójny podciąg o największej sumie w językach C++ i Python


![]() Ćwiczenie 4. Piszemy program znajdujący spójny podciąg o największej sumie
Ćwiczenie 4. Piszemy program znajdujący spójny podciąg o największej sumie
- Otwórz plik TC4_p3_c4.cpp lub TC4_p3_c4.py. Zapoznaj się z pełnym kodem programu. Objaśnij działanie poszczególnych wierszy programu.
- Uruchom program kilka razy. Jaki będzie wynik działania programu, jeżeli w danej tablicy (lub liście) znajduje się kilka spójnych podciągów niemalejących o tej samej sumie – który z nich zostanie wskazany jako wynik działania programu?
![]() Ćwiczenie 5. Modyfikujemy program znajdujący spójny podciąg o największej sumie
Ćwiczenie 5. Modyfikujemy program znajdujący spójny podciąg o największej sumie
- Otwórz plik TC4_p3_c4.cpp lub TC4_p3_c4.py.
- Zmień program tak, by znajdował spójny podciąg nierosnący o największej sumie.
- Zapisz program w pliku pod nazwą TC4_p3_c5.cpp lub TC4_p3_c5.py.
![]() Zadania
Zadania
- Napisz specyfikację zadania i zapisz listę kroków algorytmu znajdowania najdłuższego spójnego podciągu niemalejącego.
- Napisz program znajdujący najdłuższy spójny podciąg niemalejący w ciągu znaków wprowadzonych przez użytkownika.
- Napisz program znajdujący w ciągu liczb jednocześnie najdłuższy spójny podciąg malejący, najdłuższy spójny podciąg rosnący i najdłuższy spójny podciąg stały.
- Napisz specyfikację zadania i zapisz listę kroków algorytmu znajdowania spójny podciąg o największej sumie.
- Napisz program znajdujący w ciągu o długości n spójny podciąg o długości m (m < n) o największej sumie.
Wskazówka: Zastosuj pętlę zagnieżdżoną, sumowanie i sprawdzanie, czy otrzymałeś sumę większą od ostatnio zapamiętanej. - Napisz program znajdujący w ciągu liczb najdłuższy spójny podciąg o sumie zadanej przez użytkownika lub wypisujące komunikat o braku takiego podciągu.
Dla zainteresowanych
- Napisz program znajdujący w ciągu liczb wszystkie spójne podciągi składające się wyłącznie z liczb pierwszych lub informujący o braku takich podciągów. Skorzystaj z algorytmu sita Eratostenesa dla sprawdzenia pierwszości liczby.

