Właściwości arytmetyki komputerowej

Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej 2024 realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
6) ilustruje i wyjaśnia rolę pojęć, obiektów i operacji matematycznych w projektowaniu rozwiązań problemów informatycznych i z innych dziedzin, posługuje się pojęciem logarytmu;
9) wyjaśnia, jakie może być źródło błędów pojawiających się w obliczeniach komputerowych: błąd zaokrąglenia, błąd przybliżenia;

Spis treści

1. Nadmiar i niedomiar
2. Błędy obliczeń – błąd przybliżenia i zaokrąglenia
3. Stabilność algorytmów

1. Nadmiar i niedomiar

Różne operacje arytmetyczne wykonywane na liczbach mogą powodować powstanie sytuacji wyjątkowych, ponieważ liczby zapisywane są przy użyciu skończonej liczby bitów.

Przykład 1. Używanie ośmiu bitów do zapisu liczb

Obliczymy (255 + 1) w systemie dwójkowym, używając 8 bitów do zapisu poszczególnych liczb.

255 = 11111111₂
1 = 00000001₂
11111111₂ + 00000001₂ = 100000000₂

100000000₂ to w systemie dziesiętnym 256. Ponieważ mamy do dyspozycji tylko 8 bitów, wartość najstarszego bitu zostanie utracona, a wynikiem operacji dodawania będzie liczba 0. Sytuację taką można niekiedy zaobserwować w grach komputerowych, gdy np. zdobycie bardzo dużej liczby punktów w grze powoduje „przekręcenie” licznika.

Przykład 2. Występowanie nadmiaru w programach w języku C++

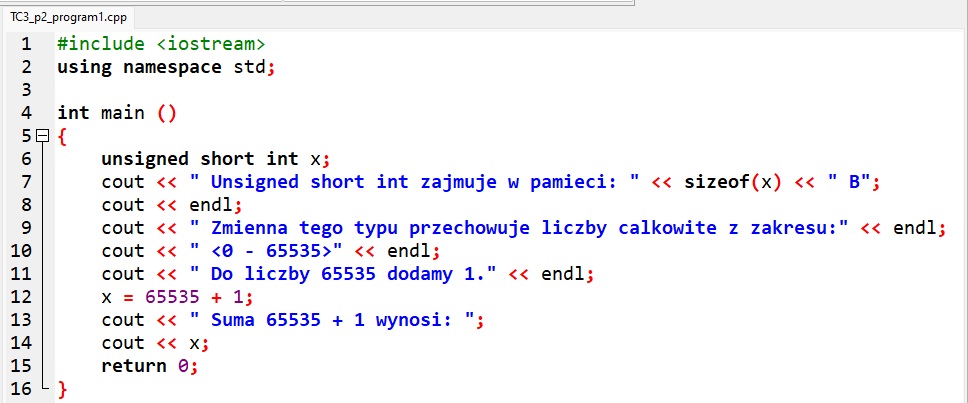
Program 1.: W programie zakres zmiennej x typu unsigned short int został przekroczony, w wyniku czego program podaje błędny wynik.

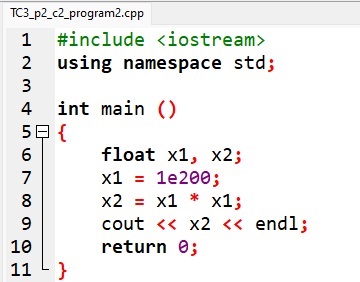
Program 2.: Program wypisuje napis „inf”. Zapis taki oznacza „nieskończoność” i sygnalizuje wystąpienie błędu nadmiaru.

Ćwiczenie 1. Analizujemy programy w języku C++, w których występuje nadmiar

1. Otwórz plik TC3_p2_c1_program1.cpp. Skompiluj i uruchom program. Objaśnij działanie programu i otrzymany wynik.
2. Otwórz plik TC3_p2_c1_program2.cpp. Skompiluj i uruchom program. Objaśnij działanie programu i otrzymany wynik.

W języku Python zmienne typu int zajmują różną liczbę bitów w zależności od wielkości zapisanej liczby. Python pozwala zapisać liczbę typu int tak dużą, jaka tylko się mieści się w pamięci komputera. W związku z tym w praktyce nie występują w języku Python problemy z nadmiarem. Rozmiar zmiennej typu int można sprawdzić funkcją sys.getsizeof(), która zwraca liczbę bitów użytych do zapisania wartości.

Przykład 3. Sprawdzanie rozmiaru zmiennej int

Z kolei typ float jest w ogromnej większości przypadków zapisywany na 64 bitach i to ogranicza zbiór liczb, które można zapisać. Informacje o ograniczeniach i działaniu arytmetyki dla typu float są dostępne w obiekcie sys.float_info.

Przykład 4. Zawartość obiektu sys.float_info

W obiekcie sys.float_info można odnaleźć największą liczbę (max)możliwą do zapisania jako float, najmniejszą dodatnią liczbą (min) możliwą do zapisania jako float oraz maksymalną liczbę cyfr dziesiętnych (dig) możliwych do zapisania jako float.

W związku z tym, że dla typu float definiuje się max i min, są w nim możliwe błędy nadmiaru i niedomiaru.

Przykład 5. Występowanie nadmiaru w języku Python dla typu float

Ćwiczenie 2. Analizujemy program w języku Python, w którym występuje nadmiar

1. Otwórz pliki TC3_p3_c2.py, TC3_p4_c2.py i TC3_p5_c2.py.
2. Uruchom każdy z programów, objaśnij działanie programu i otrzymany wynik.

Przykład 6. Występowanie niedomiaru w programach w języku C++ i Python

Efektem uruchomienia programów w językach C++ i Python jest 0.

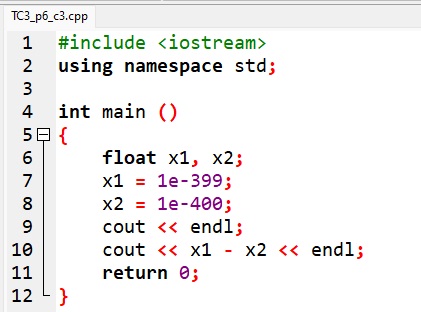
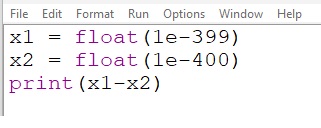
Matematycznie: 10^-399 – 10^-400 = 10^-400 · (10¹ – 1) = 9 · 10^-400.

Jednak ze względu na fakt, że liczba ta przekracza zakres dozwolonych wartości dla liczb typu float, nie może zostać dokładnie przedstawiona i jest zaokrąglana do zera (taki też jest wynik wypisywany przez program). Sytuację taką nazywamy niedomiarem (ang. underflow).

Ćwiczenie 3. Analizujemy program, w którym występuje niedomiar

1. Otwórz plik TC3_p6_c3.cpp lub TC3_p6_c3.py.
2. Uruchom program. Objaśnij działanie programu i otrzymany wynik.        

Ćwiczenie 4. Szukamy przykładów obliczeń powodujących powstanie nadmiaru lub niedomiaru

Znajdź przykłady obliczeń, które powodują powstanie nadmiaru lub niedomiaru zmiennoprzecinkowego.

2. Błędy obliczeń – błąd przybliżenia i zaokrąglenia

Jak pokazaliśmy w temacie A3, w przykładzie 4., liczby, które w systemie dziesiętnym mają skończone rozwinięcie, w systemie dwójkowym mogą mieć rozwinięcie nieskończone. W związku z tym zapis binarny niektórych liczb może być niedokładny (przybliżony). Co więcej, sposób zapisu liczb zmiennoprzecinkowych (temat A3, punkt 2.2.) determinuje liczbę cyfr znaczących, która jest ograniczona. Te dwie cechy powodują, że operacje wykonywane na liczbach zmiennoprzecinkowych są niedokładne. Innymi słowy – wyniki obliczeń są obarczone błędem.

Ćwiczenie 5. Wykonujemy obliczenia w arkuszu kalkulacyjnym

1. Oblicz w arkuszu kalkulacyjnym wartość cos 90˚. Pamiętaj, że funkcja arkusza COS() wymaga argumentu wyrażonego w radianach. Dokonaj odpowiedniej zamiany.
2. Porównaj otrzymany wynik z rzeczywistą wartością cos 90˚.

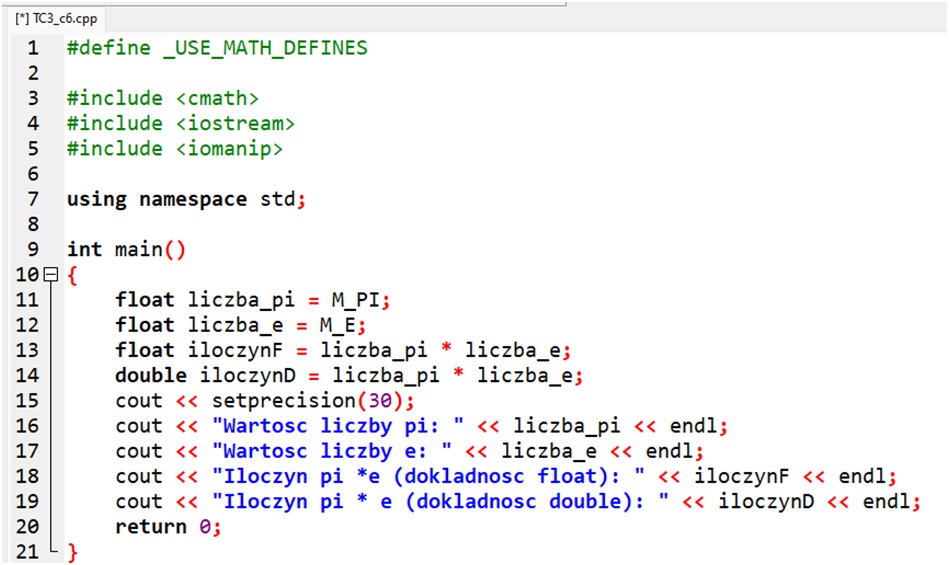
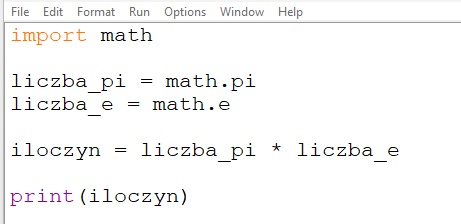
Przykład 7. Błędy obliczeń w arkuszu kalkulacyjnym i programach w języku C++ i Python

W arkuszu kalkulacyjnym Microsoft Excel:

– przybliżona wartość liczby π, uzyskana za pomocą funkcji arkusza =PI(), to 3,14159265358979;
– przybliżona wartość liczby e (podstawy logarytmu naturalnego), uzyskana za pomocą funkcji arkusza =EXP(1) to 2,71828182845905’
– iloczyn tych wartości (π • e) to 8,53973422267357.

Tymczasem rzeczywisty iloczyn powyższych wartości liczb π i eto 8,5397342226735732309665130995.

Różnica pomiędzy wartością dokładną iloczynu a wartością przybliżoną iloczynu wynika z faktu, że sposób zapisu liczb zmiennoprzecinkowych w arkuszu kalkulacyjnym pozwala na zapisanie 14 cyfr po przecinku. Mnożenie dwóch wartości zawierających 14 cyfr po przecinku powoduje powstanie wartości z 28 cyframi po przecinku: 8,5397342226735732309665130995). Może ona zostać zapisana z dokładnością 14 cyfr po przecinku, jednak jest zaokrąglana do 8,53973422267357.

Uwaga: W języku C++ wyniki będą różne zależnie od użytych wersji arkusza oraz użytego kompilatora.

Ćwiczenie 6. Wykonujemy obliczenia w arkuszu kalkulacyjnym

1. Oblicz wartość π⋅e w arkusz kalkulacyjnym.
2. Otwórz pliki TC3_p7_c6.cpp lub TC3_p7_c6.py. Porównaj wartości otrzymane w wyniku obliczeń w arkuszu kalkulacyjnym z wartościami uzyskanymi w wyniku działania programu w języku C++ lub Python.

Ćwiczenie 7. Sprawdzamy występowanie błędów obliczeń

Otwórz plik TC3_c7.cpp lub TC3_c7.py. Uruchom program. Sprawdź, dla jakich wartości początkowych x₁ program działa poprawnie (x₂ = x₁), a dla jakich powoduje wystąpienie błędów obliczeń.

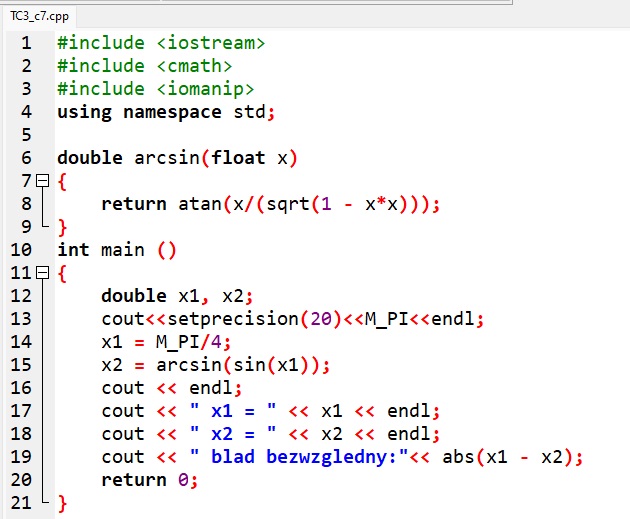
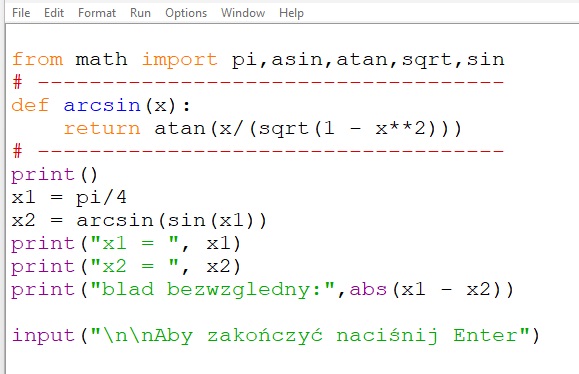
W programach z ćwiczenia 7. obliczyliśmy błąd jako wartość bezwzględną różnicy pomiędzy wartością spodziewaną obliczeń a wartością otrzymaną obliczeń. Taki błąd nazywamy błędem bezwzględnym i określamy wzorem:

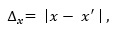
gdzie:
Δx – błąd bezwzględny,
x  –  wartość spodziewana,
x’ –  wartość otrzymana.

Często nie jest ważne, jak duży jest błąd w liczbach bezwzględnych, lecz jak bardzo wpływa on na wynik obliczeń. Cechę tę obrazuje błąd względny, rozumiany jako stosunek błędu bezwzględnego do spodziewanej wartości obliczeń:

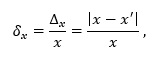
gdzie:
δ_x – błąd względny,
Δ_x – błąd bezwzględny,
x – wartość spodziewana,
x’ – wartość otrzymana.

Ćwiczenie 8. Obliczamy błąd względny i bezwzględny

Oblicz wartość pola koła dla liczby π określonej z dokładnością do 1, 2, 3, … , 10 miejsc po przecinku. Oblicz błąd względny i bezwzględny obliczeń, przyjmując jako wartość dokładną (spodziewaną) pole koła wyznaczone dla liczby π podanej z maksymalną dokładnością, na jaką pozwala arkusz kalkulacyjny w twoim komputerze. Zaobserwuj, jak zmienia się wartość błędu względnego, gdy zmieni się promień koła. Posłuż się arkuszem kalkulacyjnym.

3. Stabilność algorytmów

Błędy obliczeń same w sobie nie są na ogół niebezpieczne, o ile zdajemy sobie sprawę z możliwości ich wystąpienia. Istnieją jednak rodzaje obliczeń, w których następuje kumulacja błędów i wówczas nawet drobna (na 15. czy 20. miejscu po przecinku) zmiana wartości początkowej może prowadzić do krańcowo różnych wartości końcowych obliczeń. Algorytmy charakteryzujące się kumulowaniem błędów obliczeń nazywamy algorytmami niestabilnymi. Algorytmy, w których nie zachodzi kumulacja błędów obliczeń, nazywamy algorytmami stabilnymi.

Przykład 7. Algorytm niestabilny

Rozważmy ciąg liczbowy: x_n+1 = x²_n + C, gdzie C – stała.
Dla C = –2 i x₁ = 0,5 kolejne wyrazy tego ciągu wynoszą:
x₁ = 0,5
x₂ = –1,75
x₃ = 1,0625
x₄ = –0,87109375
x₅ = –1,2411956787109375
…

Ćwiczenie 9. Sprawdzamy stabilność algorytmu

1. Napisz program w wybranym języku programowania lub przygotuj w arkuszu kalkulacyjnym tabelę realizującą algorytm obliczający n-ty wyraz ciągu z przykładu 4. dla x₁ i n wprowadzanych przez użytkownika.
2. Oblicz dziesiąty wyraz ciągu dla x₁ = 0,5 oraz x₁’ = x₁ – 0,000001 i x₁„ = x₁ + 0,000001. Oblicz wyrazy x₂₀ i x₁₀₀dla x₁, x₁’, x₁„. Porównaj wyniki.

Dla n = 10 wartości x_n, x_n’ i x_n” są jeszcze do siebie zbliżone, ale wraz ze wzrostem n różnią się coraz bardziej. Łatwo to wyjaśnić, patrząc na tabelę z kolejnymi wartościami x_n otrzymaną w ćwiczeniu 9. Liczba cyfr znaczących, niezbędnych do dokładnego zapamiętania x_n podwaja się przy każdym zwiększeniu n o 1. Stąd nawet drobne zmiany wartości początkowej x₁ prowadzą do kumulacji błędów, a w efekcie do całkowitej utraty dokładności obliczeń.

Zadania

1. Wyjaśnij na przykładzie, kiedy w obliczeniach pojawia się sytuacja nadmiaru.
2. Dlaczego operacje na liczbach zmiennoprzecinkowych mogą być obarczone błędem? Pokaż na przykładzie.
3. Wyjaśnij na przykładzie różnicę między błędem względnym i bezwzględnym.
4. Kiedy algorytm jest stabilny, a kiedy niestabilny? Podaj przykłady.
5. Napisz niestabilny oraz stabilny program znajdujący pierwiastki równania kwadratowego ax² + bx + c = 0. Przetestuj program dla rożnych współczynników a, b, c, np. a = 1, b = 10000, c = 0,1. Porównaj wyniki otrzymane w obu programach.
   Wskazówka: Program stabilny to program, w którym współczynnik a=0  oraz jeden z pierwiastków równania obliczany jest ze wzoru:

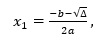
zaś drugi ze wzoru Viete’a:

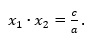
To, który pierwiastek jest obliczany ze wzoru Viete’a (x₁ czy x₂), zależy od znaku współczynnika b.