Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.
Zapisy podstawy programowej 2024 realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
- do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
- objaśnia dobrany algorytm, uzasadnia poprawność rozwiązania na wybranych przykładach danych i ocenia jego efektywność;
II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- projektuje i tworzy programy w procesie rozwiązywania problemów, wykorzystuje w programach dobrane do algorytmów struktury danych, w tym struktury dynamiczne i korzysta z dostępnych bibliotek dla tych struktur;
- sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;
- zapisuje za pomocą listy kroków lub pseudokodu i implementuje w wybranym języku programowania algorytmy poznane na wcześniejszych etapach oraz algorytmy:
f) wyznaczania miejsc zerowych funkcji metodą połowienia,
g) obliczania przybliżonej wartości pierwiastka kwadratowego,
Spis treści
- Wprowadzenie
- Wyznaczanie miejsc zerowych funkcji metodą połowienia
- Obliczanie przybliżonej wartości pierwiastka kwadratowego
- Metoda połowienia przedziału (bisekcji)
- Obliczanie wartości pierwiastka kwadratowego metodą Newtona-Raphsona
- Obliczanie przybliżonej wielkości pola obszarów zamkniętych
1. Wprowadzenie
Wykonywanie obliczeń od zawsze było jednym z zadań komputerów. Fakt, że współcześnie nawet komputery osobiste mają ogromną moc obliczeniową, tym bardziej predestynuje je do tego celu. Rozwiązywanie z pomocą komputerów problemów z różnych dziedzin naukowych, które polegają na obliczaniu wielkości zdefiniowanych za pomocą zależności matematycznych, określa się mianem algorytmów numerycznych. W kolejnych punktach przedstawimy kilka najczęściej wykorzystywanych algorytmów numerycznych (obliczeniowych).
2. Wyznaczanie miejsc zerowych funkcji metodą połowienia
Wyznaczanie miejsc zerowych funkcji f(x) to znalezienie wszystkich wartości x, dla których f(x) = 0. Dla uproszczenia przyjmiemy, że szukać będziemy miejsca zerowego funkcji w przedziale 〈a, b〉.
Istnieje kilka metod wyznaczania miejsca zerowego funkcji. Najprostsza z nich to metoda połowienia przedziału (bisekcji), która sprowadza się do zacieśniania obszaru poszukiwań przez dzielenie zadanego przedziału na połowy i rozpatrywanie tego z dwóch przedziałów, na którego krańcach wartości funkcji różnią się znakiem.
Przyjmiemy następujące warunki początkowe: funkcja f(x) jest ciągła w przedziale domkniętym 〈a, b〉 oraz f(a) i f(b) są różnych znaków (f(a) · f(b) <0). Wówczas na podstawie twierdzenia o przyjmowaniu wartości pośrednich można stwierdzić, że istnieje takie x ∈〈a, b〉, że f(x) = 0.
Jeżeli funkcja f(x) jest ciągła w przedziale domkniętym 〈a, b〉,f(a) ≠ f(b) oraz liczba p ∈ (f(a); f(b)),to istnieje taka liczba c ∈(a; b), że f(c) = p. W szczególności, jeżeli f(a) i f(b) są rożnych znaków, to istnieje takie c, że f(c) = 0.
Metoda połowienia przedziału polega na obliczeniu wartości c będącej środkiem przedziału 〈a, b〉:
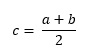
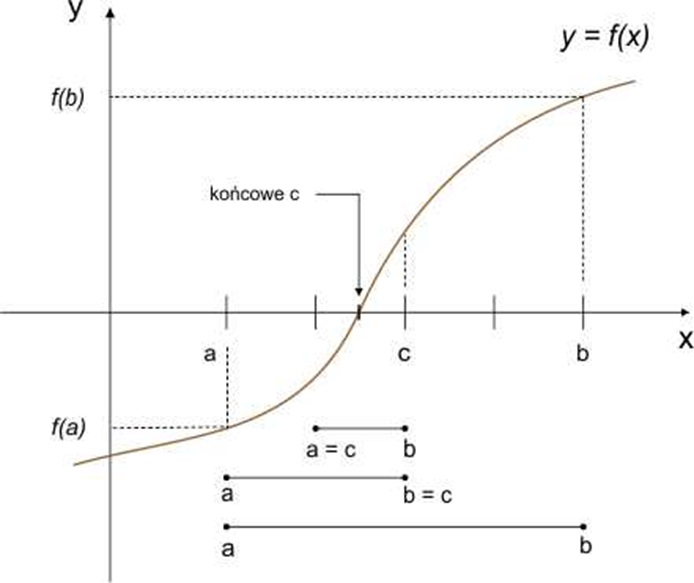
Jeśli f(c) = 0, to miejsce zerowe zostało znalezione. W przeciwnym razie wartość c staje się krańcem jednego z przedziałów. Wybieramy ten z nich, na którego krańcach wartości funkcji są różnych znaków i powtarzamy połowienie, przyjmując odpowiednio a = c lub b = c.
Warunki zakończenia algorytmu można określić na trzy sposoby:
- kiedy c osiągnie określoną wartość:
lub
- kiedy |f(c)| < d, gdzie d – założona dokładność obliczeń (błąd bezwzględny); oznacza to, że osiągnięte przybliżenie miejsca zerowego różni się od rzeczywistego co najwyżej o pewną założoną wartość d, np. ± 0,001 (w tym przypadku poprawność otrzymanego wyniku jest uzależniona od założonej dokładności (d), dlatego ważne jest dobranie tej wartości odpowiednio do rodzaju funkcji)
lub
- kiedy |b – a| < d, gdzie d – założona dokładność; oznacza to, że przedział jest tak mały, że nie ma sensu dalej go dzielić.
W pierwszym przypadku liczba iteracji (a zatem i złożoność obliczeniowa) algorytmu jest stała dla każdej funkcji, natomiast jego dokładność zmienia się (w zależności od przyjętej liczby powtórzeń połowienia oraz początkowej rozpiętości przedziału 〈a, b〉 ). W przypadku drugim i trzecim dokładność algorytmu jest stała (ustalona z góry wartość d), natomiast w zależności od funkcji zmienia się złożoność obliczeniowa algorytmu.
Metoda połowienia przedziału jest stosunkowo wolna. O wiele szybsze są metody siecznych oraz Newtona. Opis tych metod można znaleźć w Internecie lub w literaturze dodatkowej.
![]() Przykład 1. Realizacja algorytmu wyznaczania miejsc zerowych funkcji metodą połowienia
Przykład 1. Realizacja algorytmu wyznaczania miejsc zerowych funkcji metodą połowienia
Zadanie: Znajdź miejsce zerowe funkcji w danym przedziale.
Dane: dwie liczby rzeczywiste a i b, będące końcami przedziału 〈a, b〉, a < b; funkcja f(x) określona wzorem i ciągła w przedziale 〈a, b〉, spełniająca warunek f(a) · f(b) < 0, wartości funkcji na krańcach przedziału są różnych znaków; dokładność obliczeń d.
Wynik: miejsce zerowe c funkcji f(x) w przedziale 〈a, b〉.
Pseudokod algorytmu
dopóki b – a > d oraz f(a)≠ 0 oraz f(b)≠ 0 wykonuj
c ⇽ (a + b)/2
jeżeli f(a)· f(c) < 0
b ⇽ c
w przeciwnym przypadku
a ⇽ c
jeżeli f(a) = 0 zwróć a
jeżeli f(b) = 0 zwróć b
zwróć cW programie zdefiniujemy dwie funkcje:
- Funkcja o nazwie f() będzie zwracać wartość funkcji wyrażonej wzorem:
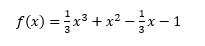
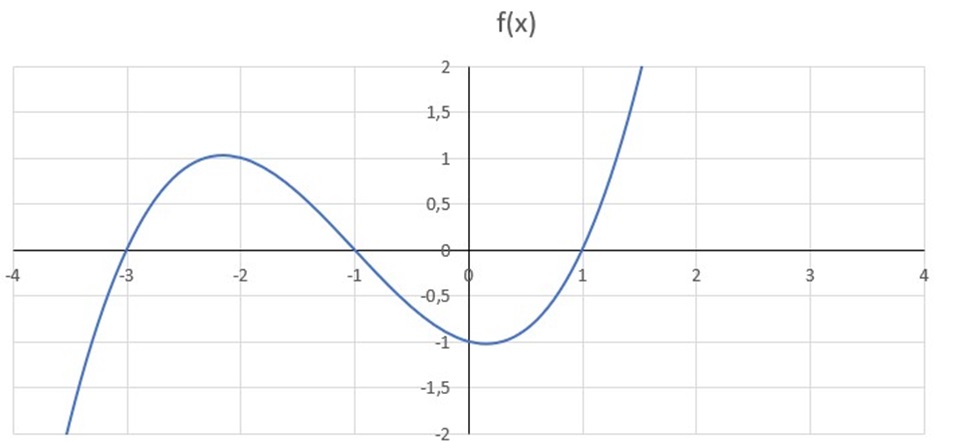
- Funkcja o nazwie m_zerowe() będzie wyznaczać miejsce zerowe funkcji f(x) w danym przedziale 〈a, b〉. W programie głównym należy zadbać o prawidłowe wprowadzenie krańców przedziału 〈a, b〉. Rozwiązanie porównamy z rozwiązaniem graficznym wykonanym w arkuszu kalkulacyjnym, przedstawionym na wykresie.
Definicje funkcji w języku programowania

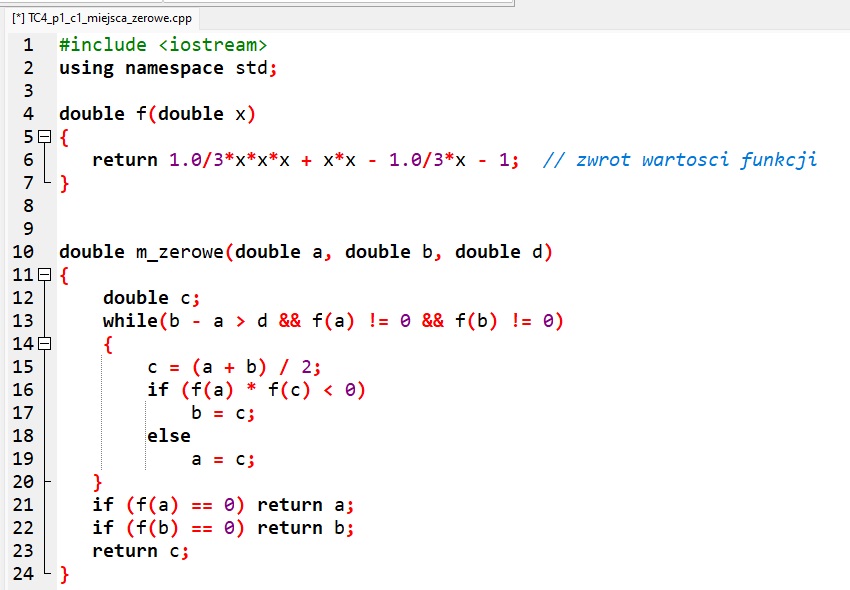

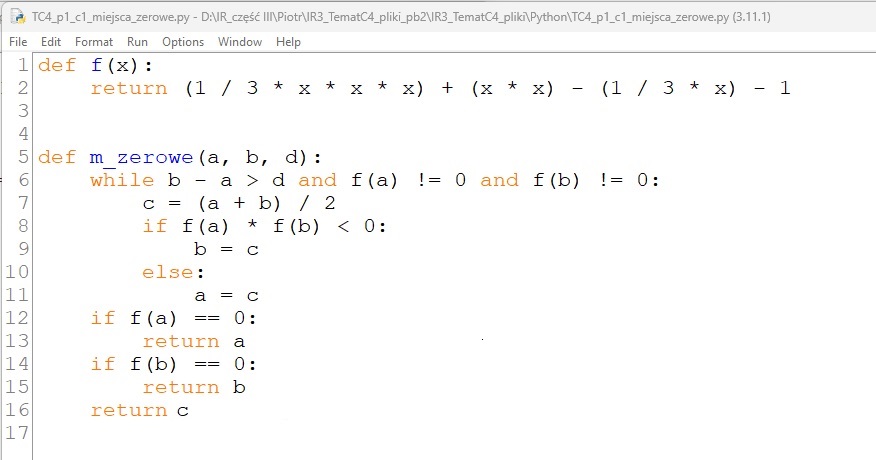
![]() Ćwiczenie 1. Piszemy program znajdujący miejsce zerowe funkcji określonej wzorem w danym przedziale 〈a, b〉
Ćwiczenie 1. Piszemy program znajdujący miejsce zerowe funkcji określonej wzorem w danym przedziale 〈a, b〉
- Otwórz plik TC4_p1_c1_miejsca_zerowe.cpp lub TC4_p1_c1_miejsca_zerowe.py. Omów działanie zdefiniowanych funkcji. Porównaj funkcję m_zerowe z pseudokodem.
- Wykorzystując funkcje f() oraz m_zerowe(), napisz program znajdujący miejsce zerowe funkcji w danym przedziale. Program nie może przyjąć krańców przedziału, jeśli nie ma w nim miejsca zerowego oraz gdy prawy kraniec przedziału b jest mniejszy lub równy lewemu krańcowi przedziału a. Program ponawia wprowadzanie krańców przedziału do momentu, aż będą spełnione warunki specyfikacji algorytmu.
- Zapisz program w pliku pod tą samą nazwą.
- Przetestuj program dla dokładności równej 0,00001 oraz:
a) a = -4, b = -2;
b) a = -2, b = 0;
c) a = 0, b= 2
oraz dla innych podanych przez ciebie danych.
3. Obliczanie przybliżonej wartości pierwiastka kwadratowego
3.1. Metoda połowienia przedziału (bisekcji)
Jednym ze sposobów obliczania pierwiastka kwadratowego z liczby nieujemnej, większej od 1 jest metoda opierająca się na algorytmie połowienia przedziału. Możemy wykorzystać do tego algorytm znajdowania miejsca zerowego funkcji f(x) = x2 – c; gdzie c jest liczbą, z której chcemy obliczyć pierwiastek kwadratowy. Miejsca zerowego poszukiwać będziemy w przedziale 〈1; c〉. Zilustrujemy to na przykładzie funkcji f(x) = x2 – 2, której wykres przedstawia poniższy rysunek.
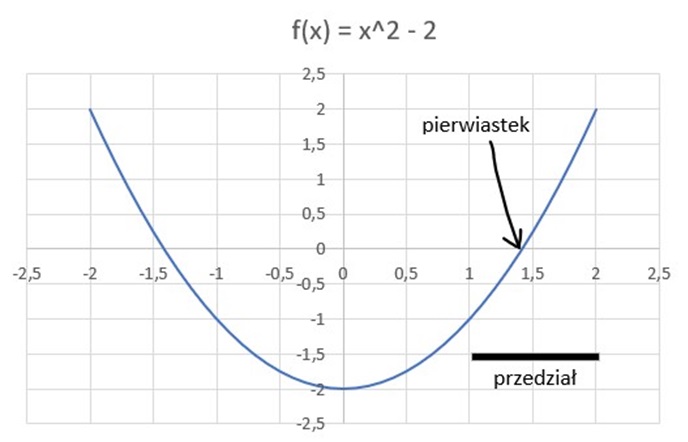
Możemy też nieco zmodyfikować algorytm wyznaczania miejsca zerowego funkcji i otrzymać algorytm wyznaczania pierwiastka kwadratowego z liczby c > 1. Chcąc wyznaczyć pierwiastek kwadratowy z liczby c (c > 1), dokonujemy wstępnego szacowania: a2 < c < b2, gdzie a i b ∈ N. Następnie znajdujemy środek s przedziału 〈a, b〉.
Sprawdzamy, czy s2 > c. Jeżeli tak, to poszukiwania kontynuujemy w lewym przedziale 〈a; s〉; jeżeli nie, to w prawym przedziale 〈s; b〉 od liczby środkowej s. Postępujemy tak, dopóki nie osiągniemy zadowalającego przybliżenia szukanej wartości pierwiastka, tzn. dopóki │s2 – c│ ≤ d , gdzie d to założona dokładność obliczeń (np. 0,01).
Metoda ta wymaga wykonania maksymalnie 9n, minimalnie n mnożeń przy zakładanej dokładności
10–n.
![]() Przykład 2. Wyznaczanie pierwiastka kwadratowego z liczby 2
Przykład 2. Wyznaczanie pierwiastka kwadratowego z liczby 2
Pierwsze szacowanie: 12 < 2 < 22.
Znajdujemy środek s przedziału 〈1; 2〉. Jest nim liczba 1,5. Podnosimy ją do kwadratu i sprawdzamy, czy otrzymana wartość jest większa od liczby podpierwiastkowej. Jeżeli tak, to połowimy przedział na lewo; jeżeli nie, to połowimy przedział na prawo od liczby środkowej. Ponieważ 1,5 2 = 2,25, więc połowimy przedział 〈1; 1,5〉. Jego środkiem jest liczba 1,25. Ponieważ 1,252 = 1,5625, więc połowimy teraz prawy przedział 〈1,25; 1,50〉. Jego środkiem jest liczba 1,375. Ponieważ 1,3752 = 1,890625, więc połowimy przedział 〈1,375; 1,500〉. Postępujemy tak, dopóki nie osiągniemy zadowalającego przybliżenia.
Zadanie: Oblicz pierwiastek kwadratowy z liczby rzeczywistej metodą bisekcji.
Dane: c – liczba rzeczywista, c > 1, d – dokładność obliczeń.
Wynik: pk – pierwiastek kwadratowy z liczby c wyliczony z dokładnością d.
Pseudokod algorytmu
a ⇽ 1
b ⇽ c
dopóki b – a > d wykonuj
pk ⇽ (a + b)/2
jeżeli pk * pk > c
b ⇽ pk
w przeciwnym przypadku
a ⇽ pk
zwróć pkNajpierw obliczamy środek przedziału (pk). Jeśli jego kwadrat jest większy od c, to poszukiwania kontynuujemy w przedziale 〈a, pk〉 (lewym), w przeciwnym przypadku w przedziale 〈pk, b〉 (prawym). Obliczenia kończymy, gdy długość przedziału jest mniejsza lub równa dokładności obliczeń d.
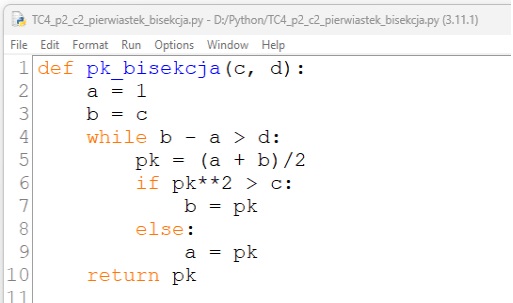
Definicje funkcji pk_bisekcja() w języku programowania

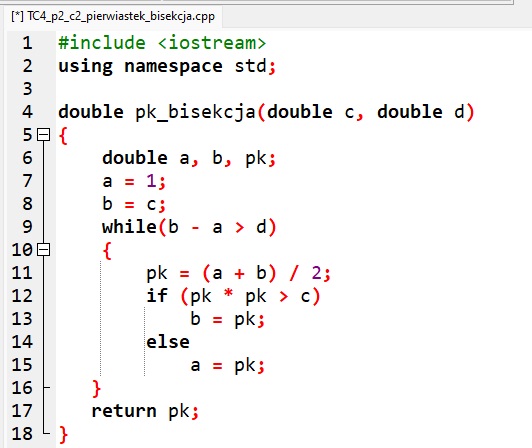

![]() Ćwiczenie 2. Piszemy program wyznaczający przybliżoną wartość pierwiastka kwadratowego
Ćwiczenie 2. Piszemy program wyznaczający przybliżoną wartość pierwiastka kwadratowego
- Otwórz plik TC4_p2_c2_pierwiastek_bisekcja.cpp lub TC4_p2_c2_ pierwiastek_bisekcja.py. Omów działanie zdefiniowanej funkcji. Porównaj funkcję z pseudokodem.
- Zapisz program w pliku pod tą samą nazwą. Przetestuj program dla różnych danych.
![]() Ćwiczenie 3. Przedstawiamy w arkuszu kalkulacyjnym realizację algorytmu obliczania przybliżonej wartości pierwiastka kwadratowego
Ćwiczenie 3. Przedstawiamy w arkuszu kalkulacyjnym realizację algorytmu obliczania przybliżonej wartości pierwiastka kwadratowego
- Przedstaw w arkuszu kalkulacyjnym realizację algorytmu obliczania przybliżonej wartości pierwiastka kwadratowego metodą bisekcji.
- Zapisz plik pod nazwą TC4_c3_pierwiastek_kwadratowy_bisekcja_w_arkuszu.
3.2. Obliczanie wartości pierwiastka kwadratowego metodą Newtona-Raphsona
Najbardziej efektywnym sposobem obliczania pierwiastka kwadratowego z liczby nieujemnej jest algorytm Newtona-Raphsona, w matematyce znany jako metoda Herona.
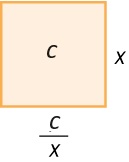
Jeżeli przyjmiemy, że liczba podpierwiastkowa c jest polem kwadratu, to bok tego kwadratu wynosi √c. Można przyjąć początkową wartość jednego boku x1 = c jako pewne przybliżenie szukanej wartości pierwiastka. Wtedy drugi bok musi być równy ![]() , aby pole kwadratu nie uległo zmianie. Oczywiście, aby dana figura pozostała kwadratem, wartości x1 i
, aby pole kwadratu nie uległo zmianie. Oczywiście, aby dana figura pozostała kwadratem, wartości x1 i ![]() powinny być równe. Jeżeli nie są, to szukana wartość √c znajduje się między nimi. Można przyjąć, że kolejne przybliżenie √c jest równe średniej arytmetycznej wartości x1 i
powinny być równe. Jeżeli nie są, to szukana wartość √c znajduje się między nimi. Można przyjąć, że kolejne przybliżenie √c jest równe średniej arytmetycznej wartości x1 i ![]() (środek przedziału 〈xi;
(środek przedziału 〈xi; ![]() 〉).
〉).
Zatem, aby wyznaczyć kolejne przybliżenia szukanej wartości pierwiastka kwadratowego z liczby c, można posłużyć się wzorem:
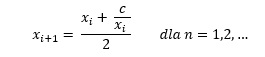
Jeżeli liczba c nie jest pełnym kwadratem liczby dodatniej, to o jakości przybliżenia pierwiastka z liczby c świadczy różnica między wartościami xi i ![]() . Jako kryterium zakończenia obliczeń można przyjąć sytuację, gdy osiągnięto założoną dokładność: │c – xi2│ ≤ d (gdzie: d – dokładność obliczeń, np. 10-11 ) lub gdy wykonano założoną z góry liczbę kroków iteracji (np. w arkuszu kalkulacyjnym).
. Jako kryterium zakończenia obliczeń można przyjąć sytuację, gdy osiągnięto założoną dokładność: │c – xi2│ ≤ d (gdzie: d – dokładność obliczeń, np. 10-11 ) lub gdy wykonano założoną z góry liczbę kroków iteracji (np. w arkuszu kalkulacyjnym).
Algorytm służący do obliczania pierwiastka n-tego stopnia z liczby c znany jest jako algorytm Newtona. W algorytmie tym do obliczania kolejnego przybliżenia szukanej wartości pierwiastka służy wzór:

gdzie:
n – stopień szukanego pierwiastka.
![]() Przykład 3. Obliczanie pierwiastka kwadratowego z liczby rzeczywistej metodą Newtona-Raphsona
Przykład 3. Obliczanie pierwiastka kwadratowego z liczby rzeczywistej metodą Newtona-Raphsona
Zadanie: Oblicz pierwiastek kwadratowy z liczby rzeczywistej metodą Newtona-Raphsona.
Dane: liczba rzeczywista c, c > 0; dokładność obliczeń d.
Wynik: pierwiastek kwadratowy p z liczby c wyliczony z dokładnością d.
Pierwiastek z liczby dodatniej (√c ) potraktujemy jako bok kwadratu o polu c. Poszukiwanie boku kwadratu o takim polu można rozpocząć od dowolnego prostokąta, którego iloczyn długości boków jest równy c. Najczęściej przyjmuje się jeden z boków o długości c, drugi o długości 1.
Pseudokod algorytmu
a ⇽ c
b ⇽ 1
dopóki |a – b| > d wykonuj
a ⇽ (a + b)/2
b ⇽ c/a
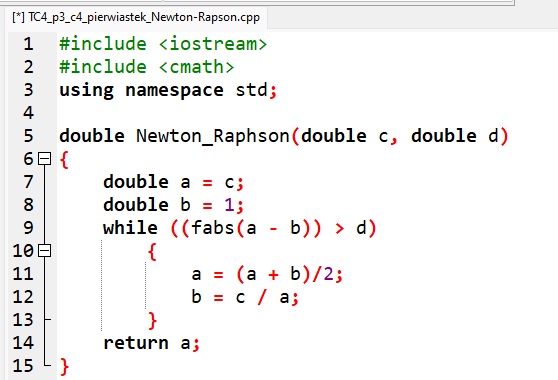
zwróć aDefinicje funkcji w językach programowania


![]() Ćwiczenie 4. Piszemy program wyznaczający wartość pierwiastka kwadratowego metodą Newtona-Raphsona
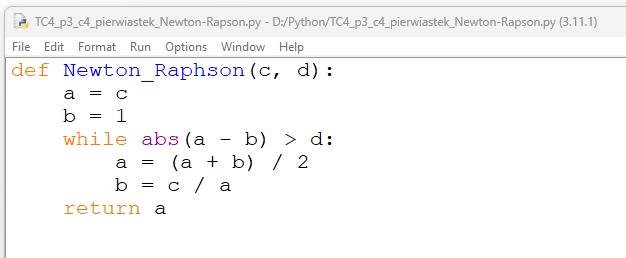
Ćwiczenie 4. Piszemy program wyznaczający wartość pierwiastka kwadratowego metodą Newtona-Raphsona
- Otwórz plik TC4_p3_c4_pierwiastek_Newton-Raphson.cpp lub TC4_p3_c4_ pierwiastek_Newton-Raphson.py. Omów działanie zdefiniowanej funkcji. Porównaj funkcję z pseudokodem.
- Wykorzystując funkcję pk_bisekcja((), napisz program obliczający przybliżoną wartość pierwiastka kwadratowego z dodatniej liczby rzeczywistej metodą Newtona-Raphsona. W programie wykorzystaj zdefiniowaną funkcję Newton_Raphson.
- Zapisz program w pliku pod tą samą nazwą. Przetestuj program dla różnych danych.
![]() Ćwiczenie 5. Przedstawiamy w arkuszu kalkulacyjnym realizację algorytmu obliczania wartości pierwiastka kwadratowego metodą Newtona-Raphsona
Ćwiczenie 5. Przedstawiamy w arkuszu kalkulacyjnym realizację algorytmu obliczania wartości pierwiastka kwadratowego metodą Newtona-Raphsona
- Przedstaw w arkuszu kalkulacyjnym implementację algorytmu obliczania przybliżonej wartości pierwiastka kwadratowego metodą Newtona-Raphsona.
- Zapisz plik pod nazwą TC4_c5_pierwiastek_kwadratowy_Newton-Raphson_w_arkuszu.
4. Obliczanie przybliżonej wielkości pola obszarów zamkniętych
Przyjmijmy, że w prostokątnym układzie współrzędnych znajduje się obszar ograniczony prostymi x = a i x = b, osią OX oraz wykresem funkcji f(x). W wielu zadaniach niezbędne jest obliczenie pola tego obszaru. Można to zrobić dokładnie za pomocą całki oznaczonej, jednak jej obliczenie dla złożonych funkcji jest zwykle trudnym zadaniem. W zastosowaniach inżynierskich zupełnie wystarczający jest wynik przybliżony (o ile przybliżenie ma odpowiednio dużą dokładność).
Jednym ze sposobów znalezienia pola obszaru jest przybliżenie jego kształtu prostokątami o rozłącznych wnętrzach. Suma pól prostokątów jest w przybliżeniu równa polu obszaru ograniczonego prostymi x = a, x = b, osią OX oraz wykresem funkcji f(x).
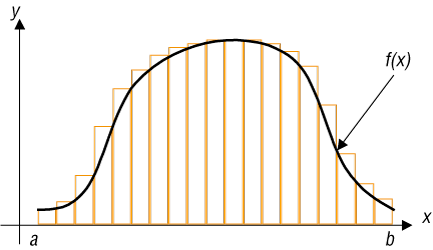
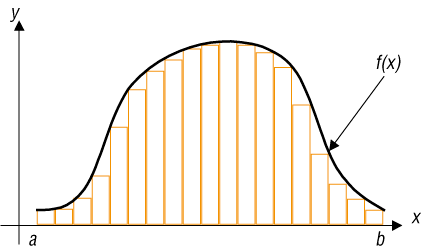
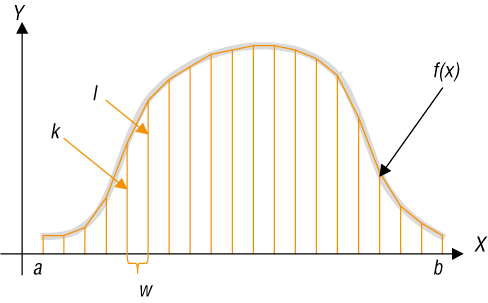
Obszar możemy pokrywać z nadmiarem (rys. 5.) – liczymy wtedy wartości funkcji f(x) dla prawych krańców przedziałów, lub z niedomiarem (rys. 6.) – liczymy wtedy wartości funkcji f(x) dla lewych krańców przedziałów. Im mniejszej liczby prostokątów użyjemy do pokrycia pola, tym mniej dokładny wynik otrzymamy (rys. 7.). W praktyce najwygodniej jest przyjąć, że wszystkie prostokąty mają boki poziome jednakowej długości i wykres funkcji przebiega przez ich środki. W ten sposób błędy nadmiaru i niedomiaru w pewnym stopniu się znoszą (rys. 8.).
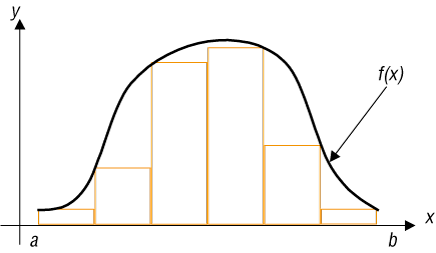
jest mniej dokładny
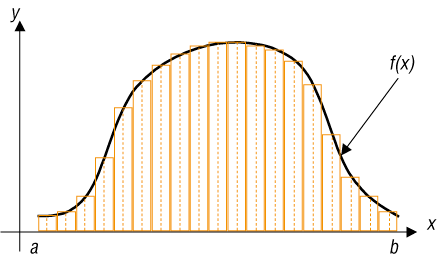
Aby skonstruować uniwersalny algorytm, musimy uwzględnić również te funkcje, które przyjmują wartości ujemne (rys. 9.). Nie wiedząc zatem, czy funkcja przyjmuje dla danego argumentu wartość dodatnią czy ujemną, jako drugi bok prostokąta będziemy przyjmować wartość bezwzględną z wartości funkcji, gdyż długość boku prostokąta nie może być wartością ujemną.
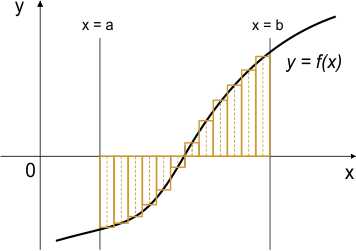
Nasze obserwacje pozwalają sformułować podstawy algorytmu obliczania przybliżonego pola obszaru ograniczonego wykresem funkcji, osią OX oraz prostymi x = a i x = b metodą prostokątów.
![]() Przykład 4. Obliczanie przybliżonego pola obszaru zamkniętego metodą prostokątów
Przykład 4. Obliczanie przybliżonego pola obszaru zamkniętego metodą prostokątów
Zadanie: Wyznacz pole obszaru ograniczonego wykresem funkcji y = f(x), prostymi x = a, x = b i osią OX.
Dane: liczby rzeczywiste a i b, a < b; liczba przedziałów n, na które dzielimy przedział 〈a, b〉; n ∈ N+, funkcja ciągła f(x) w przedziale 〈a, b〉.
Wynik: przybliżona wartość pola obszaru zamkniętego P, ograniczonego prostymi x = a, x = b oraz wykresem funkcji f(x) i osią OX.
Aby wyznaczyć pole obszaru ograniczonego wykresem funkcji f(x), osią OX oraz prostymi x = a i x = b, obliczamy najpierw szerokość w pojedynczego prostokąta:
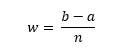
Wysokość i-tego prostokąta to wartość funkcji f(x) w punkcie o odciętej będącej środkiem poziomego boku tego prostokąta:
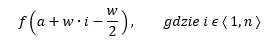
Zatem pole i-tego prostokąta wynosi:
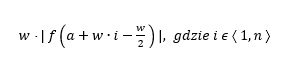
Następnie obliczamy sumę pól powierzchni prostokątów:
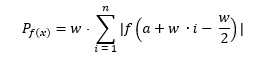
Pseudokod algorytmu
w ⇽ (b – a)/n
x ⇽ a
P ⇽ 0
dla i ⇽ 1, 2, …, n wykonuj
x ⇽ a + w × i – w / 2
P ⇽ P + w × f(x)
zwróć PDefinicje funkcji w językach programowania

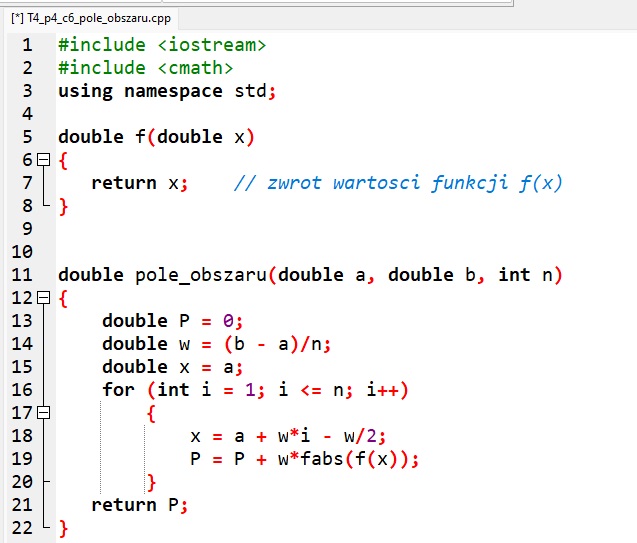


![]() Ćwiczenie 6. Piszemy program obliczający pole obszaru zamkniętego metodą prostokątów
Ćwiczenie 6. Piszemy program obliczający pole obszaru zamkniętego metodą prostokątów
- obliczający metodą prostokątów pole obszaru ograniczonego wykresem funkcji f(x), osią Ox oraz prostymi x = a i x = b. Program powinien zawierać dwie funkcje:
- 〈a, b〉 dla n prostokątów.
Dokładniejsze przybliżenie pola obszaru ograniczonego uzyskamy, zastępując prostokąt inną figurą geometryczną, np. trapezem, o wiele lepiej wpasowującym się w pochyłe fragmenty wykresu (rys. 10.).
Przyjmując takie same założenia, jak dla metody prostokątów, otrzymujemy n trapezów prostokątnych o wysokości w każdy i podstawach długości:
k = f(a + w · (i – 1)) oraz l = f(a + w · i).
Podstawiamy te dane do wzoru na pole trapezu:
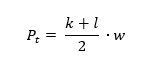
gdzie:
Pt – pole trapezu,
k, l – długości podstaw trapezu,
w – wysokość trapezu.
Sumując, otrzymujemy:
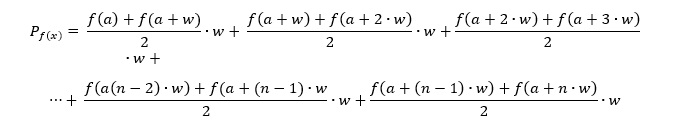
Zauważamy, że każda z wartości:
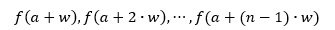
występuje dwa razy, natomiast f(a) i f(a+n·w) = f(b) występują tylko raz.
Wyciągając ![]() przed nawias, otrzymujemy wzór na wyznaczanie pola obszaru ograniczonego
przed nawias, otrzymujemy wzór na wyznaczanie pola obszaru ograniczonego
metodą trapezów:
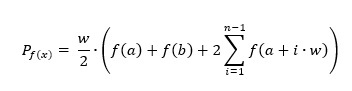
![]() Zadania
Zadania
- Omów sposób wyznaczania miejsca zerowego funkcji metodą połowienia przedziałów.
- Omów zastosowanie metody połowienia przedziałów do obliczania wartości pierwiastka kwadratowego z liczby nieujemnej.
- Wyjaśnij, na czym polega wyznaczanie pola obszaru ograniczonego metodą prostokątów.
- Wyjaśnij, na czym polega wyznaczanie pola obszaru ograniczonego metodą trapezów.
- Porównaj sposoby wyznaczania pola obszaru ograniczonego metodami prostokątów i trapezów.
- Znajdź miejsca zerowe funkcji:
a. f(x) = 3x 2 + x – 2 w przedziale x ∈ 〈0; 0,9〉,
b. f(x) = sin x + 3 cos x – 1 w przedziale x ∈ 〈0; π〉,
c. f(x) = x 3 + x 2 – 2x w przedziale x ∈ 〈–1; 0,5〉,
d. f(x) = x 3 + x 2 – 2x w przedziale x ∈ 〈0,5; 2〉,
e. f(x) = 3x 3 – 2x 2 – 3x + 2 w przedziale x ∈ 〈0; 0,9〉. - Napisz program obliczający metodą prostokątów przybliżoną wartość pola obszaru zamkniętego ograniczonego prostymi x = -2, x = 2, osią OX i funkcją f(x) = x2 – 4. Wykorzystaj program zapisany w ćwiczeniu 6., w pliku TC4_p4_c6_pole _obszaru.cpp lub TC4_p4_c6_pole_obszaru.py
- Napisz program obliczający metodą trapezów pole obszaru ograniczonego wykresem funkcji f(x), osią Ox oraz prostymi x = a i x = b. Program powinien zawierać dwie funkcje:
a. obliczającą i zwracającą wartość funkcji f(x).
b. obliczającą i zwracającą pole powierzchni w przedziale 〈a, b〉 dla n trapezów. - Wykorzystując programy z ćwiczenia 6. i zadania 7., oblicz metodą prostokątów i trapezów pole obszaru ograniczonego osią Ox, wykresem funkcji f(x) = sinx + 3cosx – 1oraz prostymi x = 0 i x=π/2. Porównaj otrzymane wartości z dokładną wartością pola, która wynosi √3 + 1. Przeprowadź w arkuszu kalkulacyjnym analizę błędów bezwzględnych i względnych obliczeń w każdej z metod, w zależności od liczby prostokątów lub trapezów. Powtórz obliczenia dla funkcji:


