Stosowanie programowania dynamicznego i grafów do rozwiązywania problemów

Wszystkie treści na stronie ir.migra.pl są chronione prawami autorskimi. Więcej informacji znajdziesz tutaj.

Zapisy podstawy programowej realizowane w temacie:

I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

2. do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;

I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:

3. objaśnia oraz porównuje podstawowe metody i techniki algorytmiczne oraz struktury danych, wykorzystując przykłady problemów i algorytmów, w szczególności:
        e) programowanie dynamiczne (do szukania najdłuższego wspólnego podciągu),
        h) grafy (do przedstawiania abstrakcyjnego modelu sytuacji problemowych).

Spis treści

1. Stosowanie programowania dynamicznego do szukania najdłuższego wspólnego podciągu
2. Grafy – wprowadzenie
3. Drzewo binarne – przykład grafu nieskierowanego

1. Stosowanie programowania dynamicznego do szukania najdłuższego wspólnego podciągu

Przykład 1. Przykłady najdłuższych wspólnych podciągów

a) Porównywane ciągi:
Ciąg 1.: INFORMATYKA
Ciąg 2.: TEORETYCZNA
Najdłuższy wspólny podciąg to ORTYA; liczba elementów takiego podciągu to 5.
b) Porównywane ciągi:
Ciąg 1.: AABCBDAAB
Ciąg 2.: AAADBD
Najdłuższe wspólne podciągi to AAAB, AADB, AABD; liczba elementów takiego podciągu to 4.

Ćwiczenie 1. Podajemy przykłady najdłuższych wspólnych podciągów

Podaj, inny niż podany w przykładzie 1., przykład dwóch ciągów i ich najdłuższych wspólnych podciągów.

Przykład 2. Wyszukiwanie najdłuższych wspólnych podciągów (dalej: NWP) z wykorzystaniem programowania dynamicznego

Zadanie: Wyszukaj najdłuższy wspólny podciąg (dalej: NWP) z wykorzystaniem programowania dynamicznego.
Dane: ciąg A o długości n znaków oraz ciąg B o długości m znaków.
Wynik: wszystkie wspólne podciągi ciągu A i ciągu B.

W algorytmie wykorzystamy tablicę (listę) pomocniczą C o wymiarach (n + 1) × (m + 1). W tablicy (liście) pamiętać będziemy długość NWP aktualnie badanych podciągów. Precyzyjniej, zakładając, że ciąg A zawiera znaki o numerach [1..n], a ciąg B – znaki o numerach [1..m], element tablicy (listy) C o indeksach [i][j] zawierać będzie długość NWP podciągów A[1..i] i B[1..j].

W algorytmie przeglądamy w pętli ciągi A i B (pętla zagnieżdżona), sprawdzając, czy znak ciągu A na pozycji i oraz znak ciągu B na pozycji j są takie same. W takiej sytuacji długość znalezionego NWP rośnie o 1, co zapamiętujemy w tablicy (liście):
C[i][j] = C[i - 1][j - 1] + 1
Jeżeli znaki są różne, to sprawdzamy, która z do tej pory wyznaczonych długości NWP jest większa i ją zapamiętujemy w tablicy (liście):
C[i][j] = max(C[i][j – 1], C[i – 1][j])
Wiersz i kolumnę o indeksie 0 wykorzystamy jako pomocnicze, zawierające 0 (długości NWP na początku algorytmu).

Dla ciągów AABCBDAAB (długość: 9 znaków) i AAADBD (długość: 6 znaków) algorytm będzie wyglądał następująco:

Krok 1. – inicjalizacja tablicy (listy) C

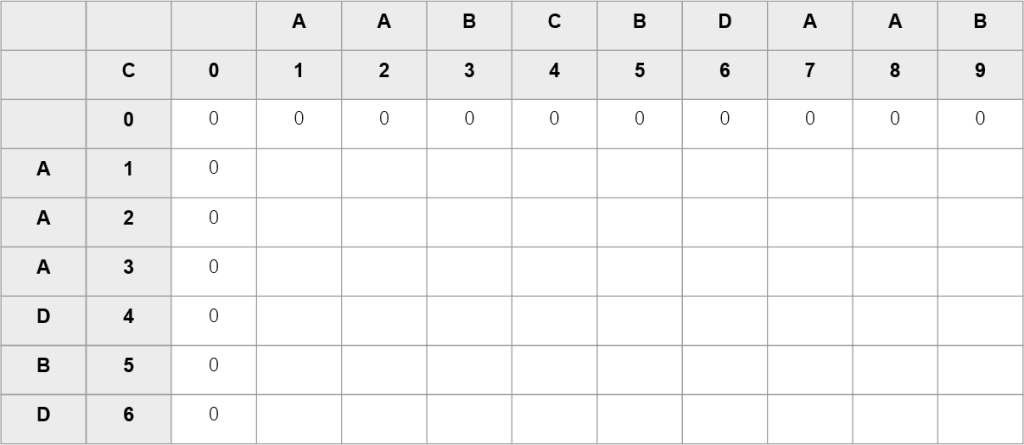
Krok 2.  – iteracja dla i = 1, j = 1: porównujemy pierwszy znak ciągu A z pierwszym znakiem ciągu B. Znaki są równe, zatem wykonujemy operację C[1][1] = C[0][0] + 1

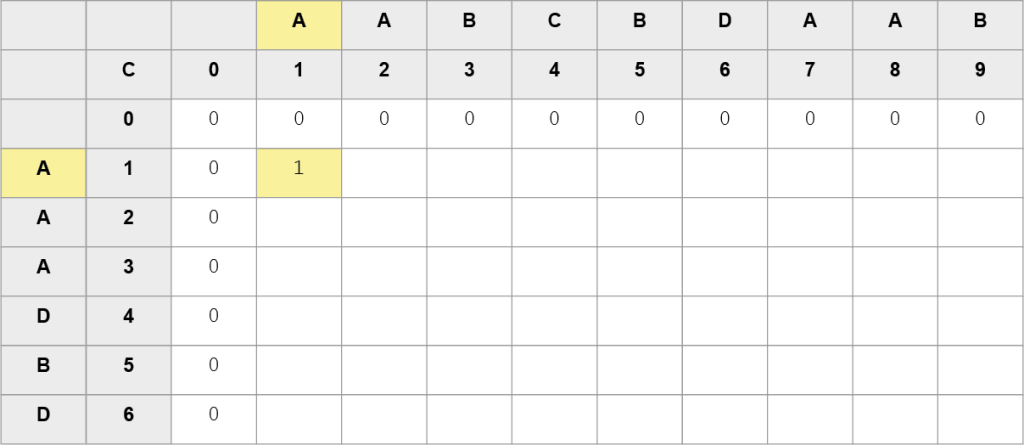
Krok 3. – iteracja dla i = 2, j = 1: porównujemy drugi znak ciągu A z pierwszym znakiem ciągu B. Znaki są równe, zatem wykonujemy operację C[2][1] = C[1][0] + 1

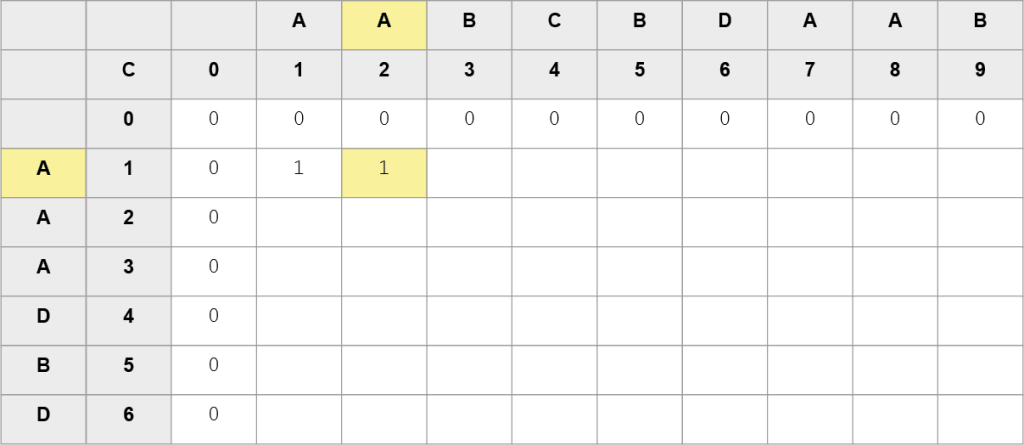
Krok 4. – iteracja dla i = 3, j = 1: porównujemy trzeci znak ciągu A z pierwszym znakiem ciągu B. Znaki są różne, zatem wykonujemy operację: C[3][1] = max(C[3][0], C[2][1])

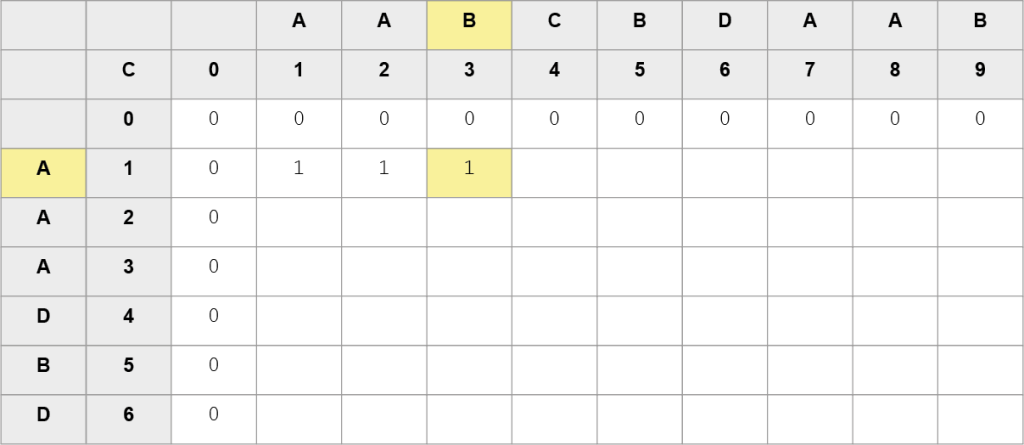
Po zakończeniu pętli tablica (lista) C powinna wyglądać następująco:

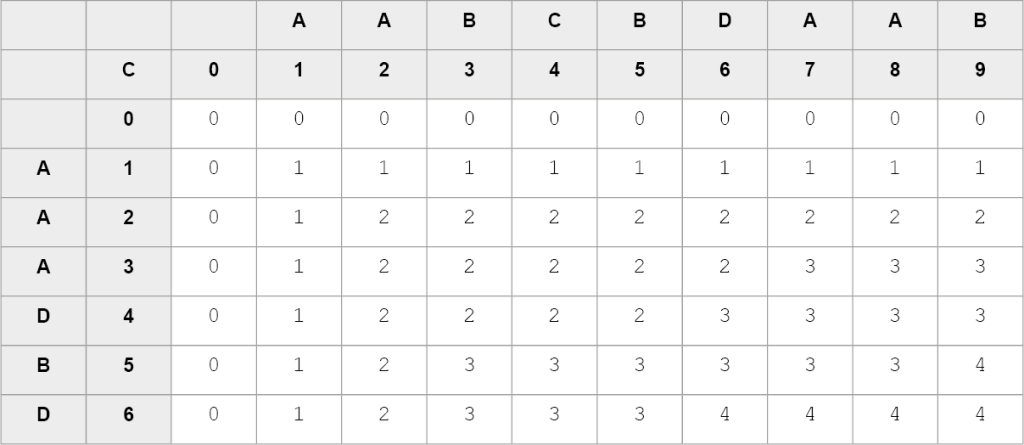
Największa wartość w tablicy (listy) C to 4, co oznacza, że NWP ma taką właśnie długość. Aby wyznaczyć taki NWP, zaczynamy przeglądanie tablicy (listy) C od ostatniego elementu. Jeżeli wartości na lewo lub w górę od danego elementu są takie same, to wybieramy jeden z tych elementów (NWP może być kilka, każda droga odpowiada innemu NWP). Jeżeli wartości po lewej i do góry są mniejsze od danego elementu, to literę odpowiadającą danemu elementowi dopisujemy z przodu do ciągu wyjściowego i przechodzimy po przekątnej w lewo w dół. Operację powtarzamy aż dojdziemy do elementu [0][0]. Wyznaczone trasy odpowiadają wszystkim NWP.

Trasa 1.

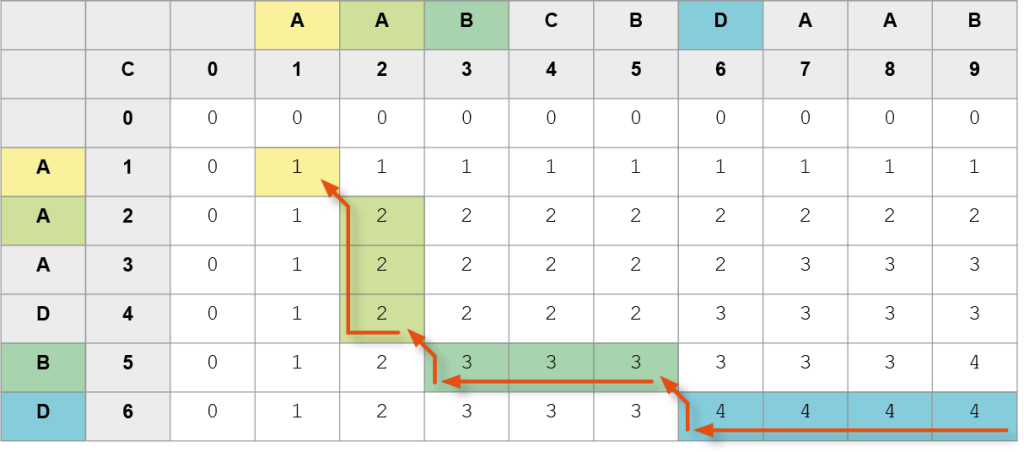
Kolejne znaki NWP (od końca): D, B, A, A, a zatem NWP to AABD.

Trasa 2.

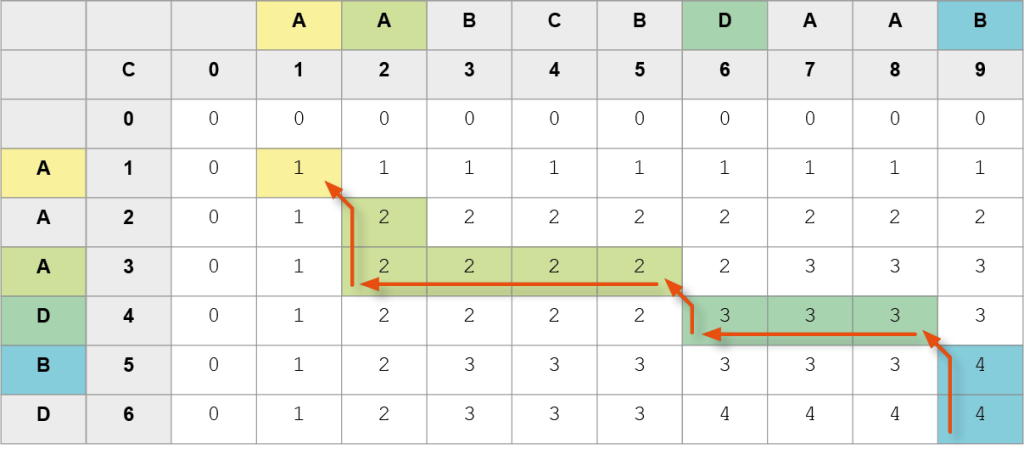
Kolejne znaki NWP (od końca): B, D, A, A, a zatem NWP to AADB.

Trasa 3.

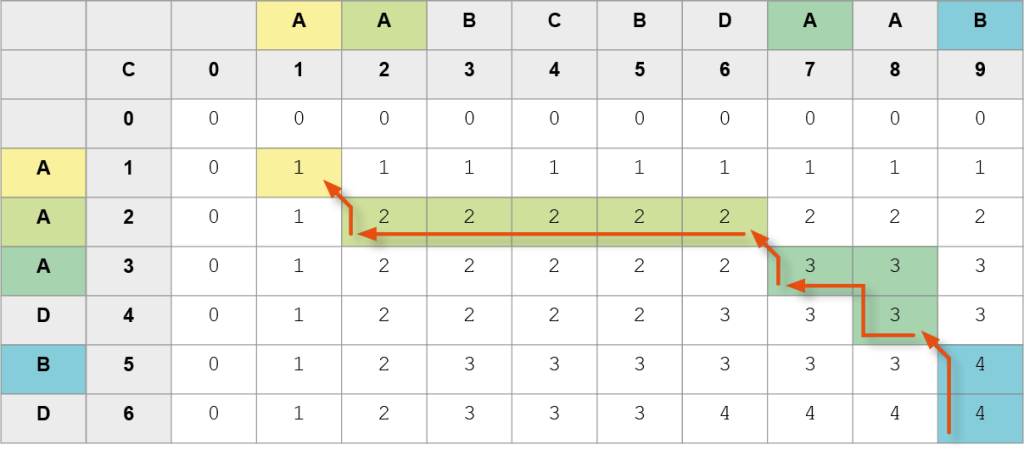
Kolejne znaki NWP (od końca): B, A, A, A, a zatem NWP to AAAB.

Trasa 4.

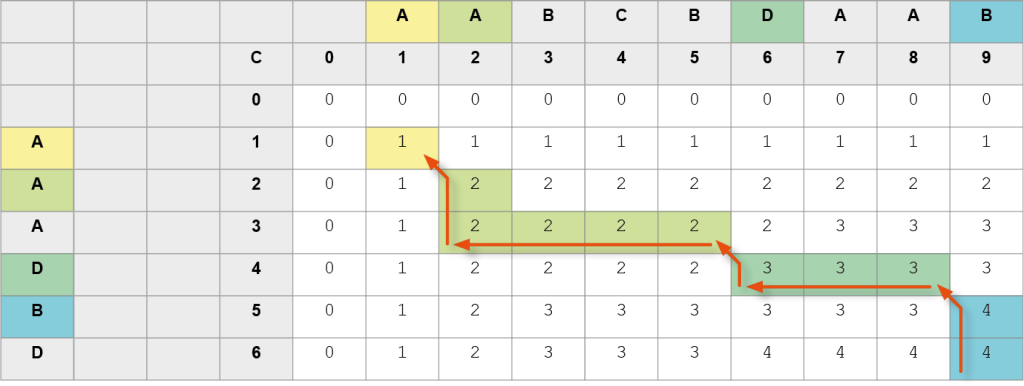
Kolejne znaki NWP (od końca): B, D, A, A, a zatem NWP to AADB.

Ćwiczenie 2. Tworzymy tablicę (listę) pomocniczą

1. Jak będzie wyglądać tablica (lista) C dla ciągów: A = „KOMPUTER” i B = „KOTEK”? Utwórz:
   a. tablicę, korzystając z arkusza kalkulacyjnego (skorzystaj z formuły warunkowej)
   lub
   b. napisz program w wybranym języku programowania tworzący tablicę (listę) pomocniczą do pamiętania długości NWP aktualnie badanych podciągów; w przykładzie 2. pokazano przykładowe programy, które zapisano w plikach TC10_p2.cpp lub TC10_p2.py.

Przykład 3. Program tworzący i wyświetlający na ekranie tablicę pomocniczą

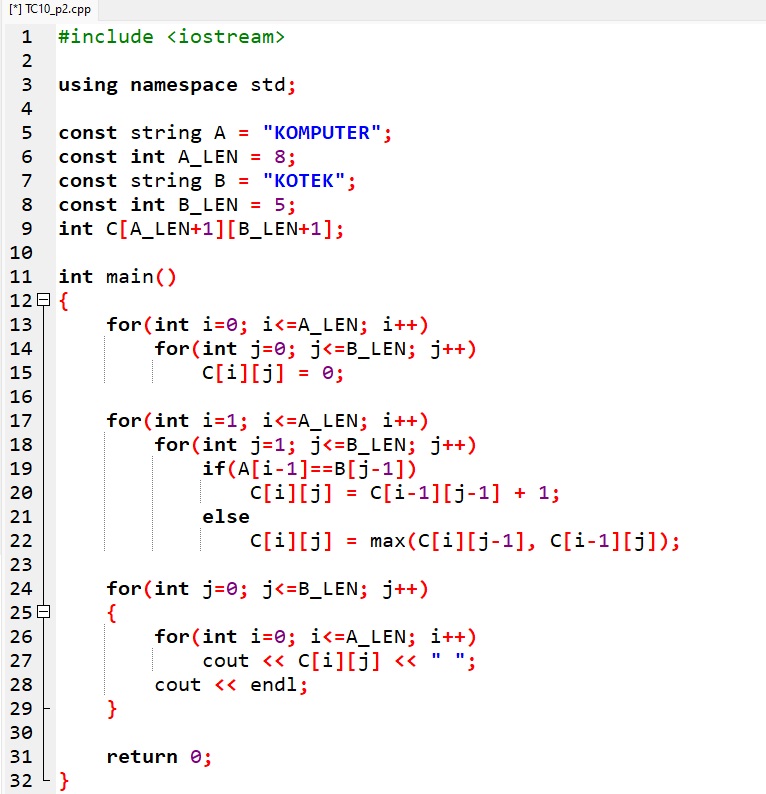
To wynik:

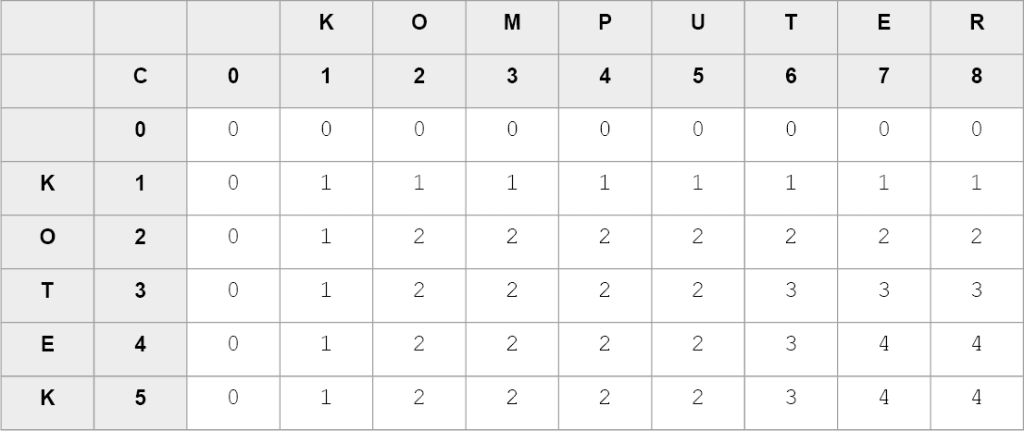
To NWP:

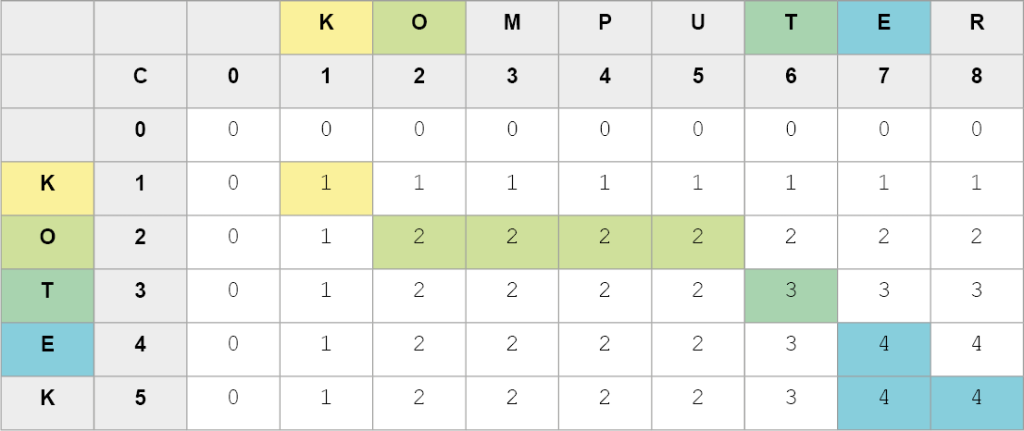
 E, T, O, K -> KOTE

Ćwiczenie 3. Wyznaczamy NWP

1. Wyznacz NWP dla ciągów z ćwiczenia 1. w podobny sposób jak pokazano w przykładzie
2. Wykorzystaj też odpowiedni program tworzący pomocniczą tablicę z przykładu 2. zapisany w pliku TC10_p2.cpp lub TC10_p2.py.

Do utworzenia programu komputerowego wyznaczającego NWP można wykorzystać metodę „dziel i zwyciężaj” oraz technikę rekurencji. Definiujemy funkcję zwracającą kolejny znaki NWP, której parametrami będą końcowe indeksy tablicy (listy). Na początku funkcję wywołujemy z parametrami n i m (w naszym przykładzie – 8 i 5). Po znalezieniu wszystkich komórek tablicy (listy) zawierających liczbę odpowiadającą długość NWP (dla naszego przykładu – 4), uzyskamy indeksy ostatniej komórki zawierającej daną wartość (w naszym przykładzie – 7 i 4). Te wartości, pomniejszone o 1, wykorzystamy w rekurencyjnym wywołaniu funkcji jako nowe „końcowe” indeksy tablicy (listy).

2. Grafy – wprowadzenie

Wierzchołki grafu mogą być numerowane i reprezentować konkretne obiekty, a krawędzie – relacje między nimi. Dzięki temu za pomocą grafu można modelować różne sytuacje problemowe.

Przykład 4. Przekształcenie schematu mostów w graf

Jednym z pierwszych problemów, do których zastosowano teorię grafów, jest problem mostów królewieckich, opisany w roku 1741 przez Leonharda Eulera. Na rysunku 1. przedstawiono schematycznie układ tych mostów i odpowiadający im graf. Wyspa z lewej strony to lewy wierzchołek grafu, a wyspa z prawej to prawy wierzchołek grafu. Brzegi rzeki to górny i dolny wierzchołek grafu. Połączenia pomiędzy wierzchołkami to mosty.

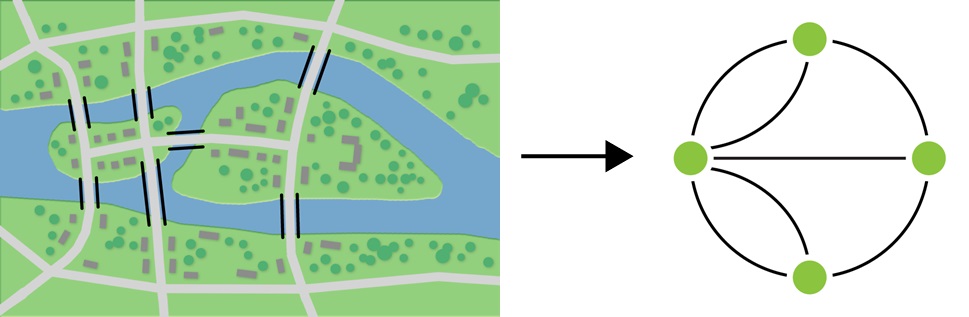
Rys. 1. Schematyczny rysunek mostów królewieckich i graf, w który przekształcono ten schemat mostów

Grafy można wykorzystać np. do reprezentacji połączeń między miastami. Wówczas wierzchołki grafu będą reprezentować miasta, a krawędzie grafu – drogi pomiędzy miastami. Każda krawędź będzie miała przypisaną liczbę, oznaczającą długość danego odcinka. Grafy umożliwiają również znajdowanie najlepszej drogi z danego miejsca do miejsca docelowego – wykorzystywane są w programach obsługujących urządzenia GPS i w grach komputerowych.

Jeśli krawędzie grafu mają wyznaczony kierunek, graf nazywamy skierowanym (między wierzchołkami można „przemieszczać” się wyłącznie w określonym kierunku). Natomiast, jeśli z każdego wierzchołka można dotrzeć do każdego innego wierzchołka (tylko w jeden sposób), mówimy o grafie nieskierowanym. Graf przedstawiony na rysunku 1. jest grafem nieskierowanym.

Przykładem grafu nieskierowanego jest drzewo, w tym drzewo binarne. Na przykładzie takiego drzewa pokażemy m.in. dodawanie nowego elementu do drzewa, przeglądanie drzewa, wypisywanie elementów drzewa w posortowanej kolejności.

3. Drzewo binarne – przykład grafu nieskierowanego

Wierzchołki drzewa binarnego będziemy nazywać, tak jak w liście jednokierunkowej, węzłami (elementami końcowymi lub liśćmi).

Węzeł drzewa jest strukturą (w języku C++) składającymi się z trzech pól: Dane, lewy i prawy. Wartościami pól lewy i prawy są wskaźniki: pusty lub wskaźnik do syna.

W języku Python węzły można reprezentować jako obiekty klasy zawierającej pola podobne jak w języku C++.

Szczególnym przypadkiem drzewa binarnego jest binarne drzewo poszukiwań (zwane też drzewem uporządkowanym), w którym wartość pola Dane ojca jest nie mniejsza niż wartość zmiennej Dane u syna lewego i mniejsza niż u syna prawego (rys. 2.).

Binarne drzewa poszukiwań można zastosować do rozwiązywania problemów, w których musimy szybko posortować elementy lub wyszukać, na przykład w różnego rodzaju słownikach.

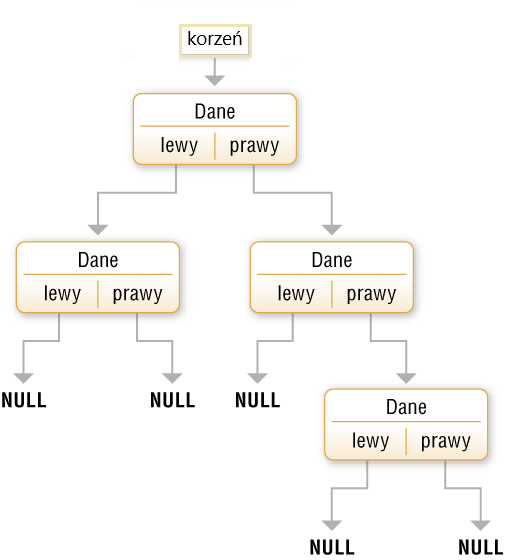
Rys. 2. Schemat drzewa binarnego

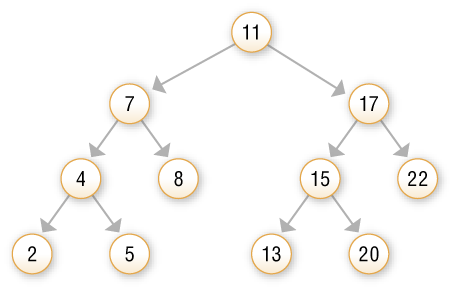
Rys. 3. Schemat binarnego drzewa poszukiwań

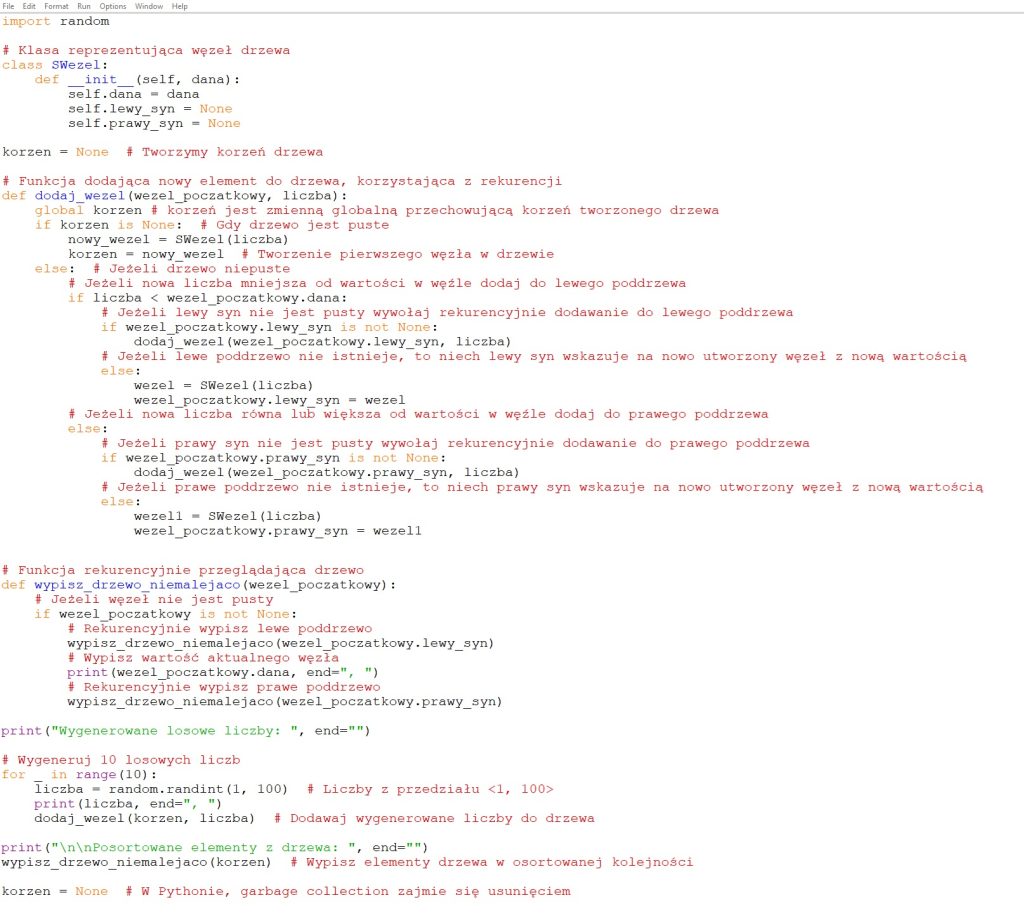
Przykład 5. Tworzenie i przeglądanie binarnego drzewa poszukiwań

Program zapisany w pliku TC10_p2.cpp zawiera przykładową implementację binarnego drzewa poszukiwań dla wartości liczbowych w języku C++.
W kodzie programu struktura SWezel reprezentuje węzeł drzewa zawierający pole do przechowywania wartości liczbowej dana oraz dwa wskaźniki: lewego syna i prawego syna.

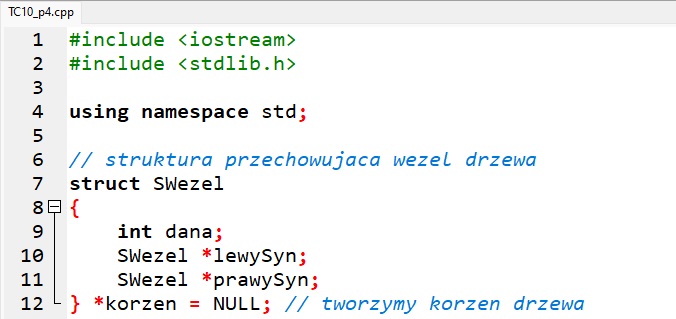
Funkcja stworzNowyWezel tworzy i inicjalizuje zmienną dynamiczną typu SWezel, z wartością liczbową pochodzącą z parametru liczba.

Kod zawiera także funkcję dodajWezel, której zadaniem jest dodawanie wartości do drzewa, zgodnie z zasadą, że element mniejszy jest wstawiany jako lewy syn sprawdzanego węzła. Funkcja najpierw sprawdza, czy drzewo nie jest puste, a jeżeli jest, dodaje pierwszy węzeł, który staje się korzeniem. Jeżeli drzewo nie jest puste, to porównujemy wstawianą wartość z wartością z aktualnego węzła. Jeżeli wartość jest mniejsza, sprawdzamy, czy istnieje lewy syn drzewa. Jeżeli istnieje, rekurencyjnie wywołujemy dodawanie węzła, z tym że aktualnym węzłem staje się lewy syn.

Natomiast w przypadku, gdy lewy syn jest pusty, wskazujemy nim na nowy węzeł.

Analogicznie algorytm wygląda w przypadku, gdy wartość wstawiana jest większa lub równa aktualnemu węzłowi, z tym że to prawy syn wskazuje na nowy węzeł lub jest parametrem rekurencyjnego wywołania.

Funkcja wypiszDrzewoNiemalejaco przechodzi rekurencyjnie drzewo, wyświetlając elementy w porządku niemalejącym.

W funkcji main programu generujemy losowo 10 liczb z przedziału od 1 do 100 i wstawiamy do drzewa. Następnie, aby zaprezentować poprawność uporządkowania w drzewie, wyświetlamy kolejno posortowane elementy drzewa.

W programie w języku Python węzły reprezentujemy poprzez obiekty klasy SWezel zawierającej pola podobne, jak w programie w języku C++.

Implementacja programu tworzącego i przeglądającego binarne drzewo poszukiwań jest podobna do implementacji w języku C++. Jedyną różnią jest brak oddzielnej funkcji do tworzenia węzła, ponieważ jej implementacja jest już zawarta w funkcji __init__.

Uwaga: Nazwa __init__ to specjalna nazwa zarejestrowana dla tzw. konstruktora, tj. funkcji wywoływanej w momencie utworzenie obiektu należącego do danej klasy. W języku C++ również istnieje możliwość wykorzystania konstruktorów, przy programowaniu obiektowym.

Ćwiczenie 4. Analizujemy kod programu zawierający implementację binarnego drzewa poszukiwań w języku C++

1. Otwórz plik TC10_p4.cpp lub TC10_p4.py. Przeanalizuj kod programu i komentarze oraz omów, jakie zadania rozwiązują poszczególne funkcje.
2. Uruchom program i wykonaj go.

Ćwiczenie 5. Modyfikujemy program

1. Otwórz plik TC10_p4.cpp lub TC10_p4.py. Dodaj do programu funkcję wypiszDrzewoNierosnaco, która wyświetli elementy drzewa w kolejności nierosnącej.
2. Zapisz program w pliku pod nazwą TC10_p4_c5.cpp lub TC10_p4_c5.py.

Przykład 6. Wyszukiwanie wartości w binarnym drzewie poszukiwań

Aby wyszukać w drzewie podaną wartość, przeglądamy drzewo, począwszy od korzenia.

Jeżeli szukana wartość jest równa wartości zapisanej w węźle, to wartość została znaleziona i algorytm kończy się. Jeżeli szukana wartość jest mniejsza od wartości w węźle, sprawdzamy wskaźnik do lewego syna. Jeżeli jest on pusty, to wartość nie została znaleziona i algorytm kończy się. Jeżeli wskaźnik nie jest pusty, powtarzamy operację dla lewego syna.

Jeżeli szukana wartość jest większa od wartości w węźle, to analogiczne operacje wykonujemy dla prawego syna.

Uwaga: Algorytm wyszukiwania można zaimplementować z wykorzystaniem iteracji lub rekurencji.

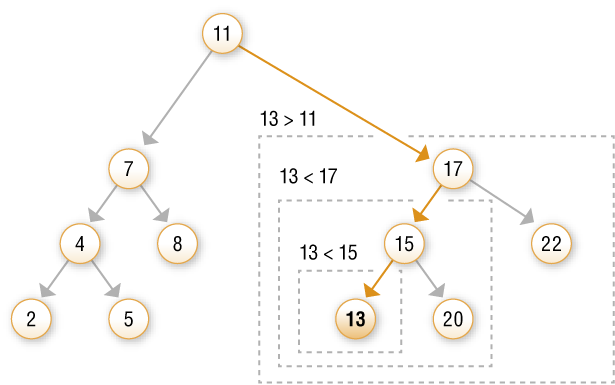
Rys. 4. Wyszukiwanie podanej wartości (tu liczby 13) w binarnym drzewie poszukiwań (przykład 5.)

Ćwiczenie 6. Analizujemy algorytm wyszukiwania w binarnym drzewie poszukiwań

Przeanalizuj i omów sposób wyszukiwania podanej wartości (liczby 5) w binarnym drzewie poszukiwań, posługując się schematem z rysunku 4.

Zadania

1. Otwórz plik TC10_p4_c5.cpp zapisany w ćwiczeniu 5. Rozbuduj program o funkcję wyszukiwania danej wartości i samego programu o interakcję z użytkownikiem. Zapisz program w pliku pod nazwą TC10_p4_z1.cpp.
   Dla zainteresowanych
2. Napisz program realizujący algorytm wyznaczania wszystkich NWP dla podanych przez użytkownika ciągów A i B.
3. Korzystając z innych źródeł, zapoznaj się z problemem mostów królewieckich opisanych przez Leonharda Eulera.