Wszystkie treści na stronie ir.migra.pl chronione są prawami autorskimi. Więcej informacji znajdziesz tutaj.
Zapisy podstawy programowej 2024 realizowane w temacie:
I. Rozumienie, analizowanie i rozwiązywanie problemów.
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:II. Programowanie i rozwiązywanie problemów z wykorzystaniem komputera i innych urządzeń cyfrowych.
- w zależności od problemu rozwiązuje go, stosując metodę wstępującą lub zstępującą;
- do realizacji rozwiązania problemu dobiera odpowiednią metodę lub technikę algorytmiczną i struktury danych;
- objaśnia dobrany algorytm, uzasadnia poprawność rozwiązania na wybranych przykładach danych i ocenia jego efektywność;
Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- projektuje i tworzy rozbudowane programy w procesie rozwiązywania problemów, wykorzystuje w programach dobrane do algorytmów struktury danych, w tym struktury dynamiczne i korzysta z dostępnych bibliotek dla tych struktur;
- sprawnie posługuje się zintegrowanym środowiskiem programistycznym przy pisaniu, uruchamianiu i testowaniu programów;
I + II. Zakres rozszerzony. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
- wykorzystuje znane sobie algorytmy przy rozwiązywaniu i programowaniu rozwiązań następujących problemów:
b) wykonywania działań na liczbach w systemach innych niż dziesiętny,
Spis treści
- Programowanie algorytmów dodawania i odejmowania na liczbach innych niż dziesiętny
- Programowanie algorytmów mnożenia i dzielenia na liczbach innych niż dziesiętny
1. Programowanie algorytmów dodawania i odejmowania na liczbach innych niż dziesiętny
Programowanie algorytmów dodawania i odejmowania omówimy na przykładzie systemu dwójkowego.
![]() Ćwiczenie 1. Przypominamy wykonywanie pisemnych działań arytmetycznych
Ćwiczenie 1. Przypominamy wykonywanie pisemnych działań arytmetycznych
Przypomnij sobie, jak pisemnie wykonuje się podstawowe działania arytmetyczne: dodawania, odejmowanie, mnożenie, dzielenie.
![]() Przykład 1. Dodawanie liczb dwójkowych w językach C++ i Python
Przykład 1. Dodawanie liczb dwójkowych w językach C++ i Python
Do przechowywania wartości liczb w systemie binarnym użyjemy typu string. Jeden znak ciągu tekstowego odpowiadać będzie jednej cyfrze („0” lub „1”). Ten sposób zapisu pozwala również na przechowywanie wartości liczb zapisanych w innych systemach liczbowych, np. systemie szesnastkowym.
Zdefiniujemy dwie funkcje pomocnicze:
DigitToInt()– zwracającą wartość liczbową znaku przekazanego jako parametr. Wykorzystamy litery, by umożliwić zapis liczb w systemach o podstawie większej niż 10, aż do podstawy 36 (10 cyfr i 26 liter alfabetu łacińskiego);IntToDigit()– zwracającą znak reprezentujący liczbę przekazaną jako parametr. W tej funkcji również wykorzystamy litery do reprezentowania liczb większych niż 9.

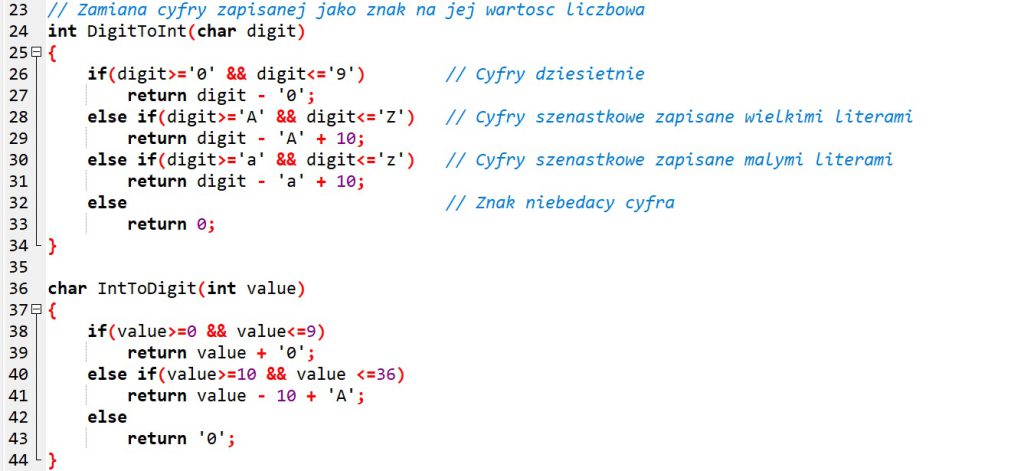

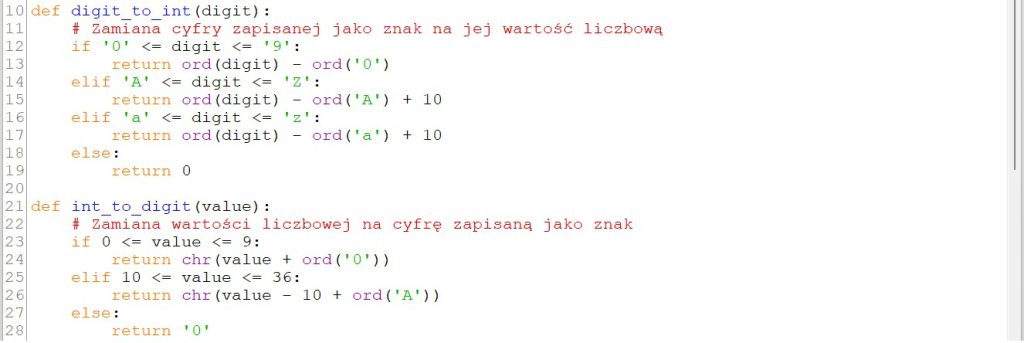
Aby móc łatwo zweryfikować poprawność wykonania operacji arytmetycznych, zdefiniujemy funkcje konwersji:
AnyBaseToDec()– zamieniającą wartość w danym systemie liczbowym, zapisaną jako ciąg znaków, na liczbę całkowitą dziesiętną;DecToAnyBase()– zamieniającą wartość całkowitą w systemie dziesiętnym na jej reprezentację w wybranym systemie liczbowym, zapisaną w postaci ciągu znaków.



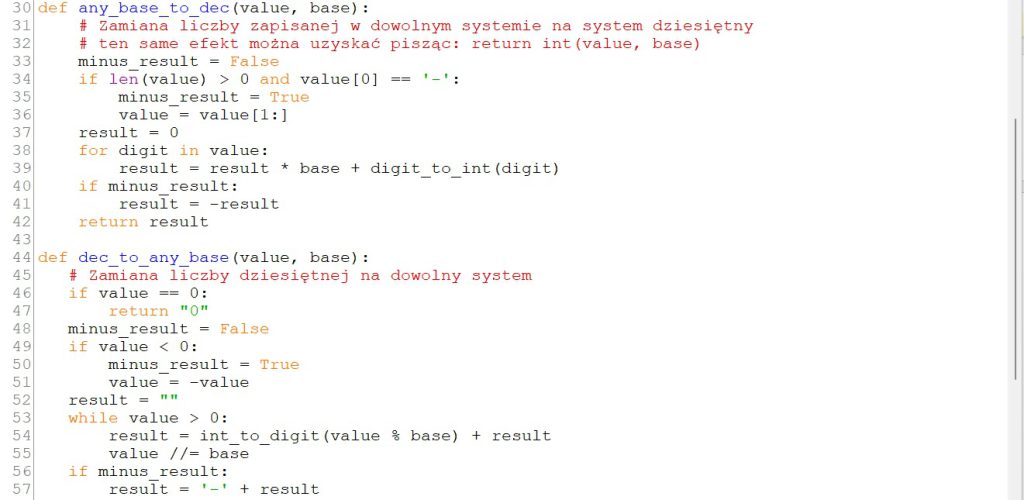
Obydwie funkcje uwzględniać będą również liczby ujemne, które w ciągu tekstowym będą miały na samym początku znak minus („-”).
Do zaprogramowania operacji dodawania potrzebujemy jeszcze funkcji pomocniczej PadLeft(), która uzupełni ciąg tekstowy przekazany jako parametr odpowiednią liczbą znaków z lewej strony. Wykorzystamy tę funkcję do dodania odpowiedniej liczby znaków „0” na początku tekstowego zapisu liczby tak, aby obydwa operandy miały taką samą długość (pozwoli to na uproszczenie algorytmu dodawania i odejmowania). Aby zapis wyniku był czytelniejszy, zdefiniujemy funkcję StripLeft() usuwającą wybrane znaki (w tym przypadku znaki „0”) z lewej strony tekstu.
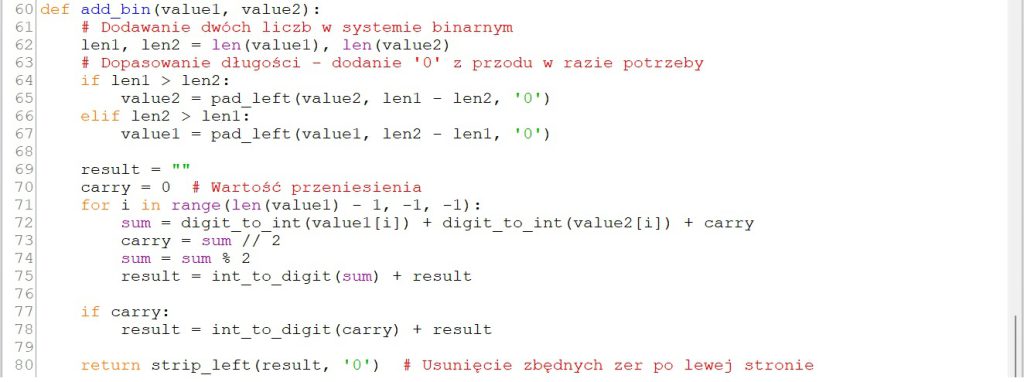
Za właściwe dodawanie odpowiada funkcja AddBin(), której parametrami są dwie liczby zapisane w systemie binarnym (parametry value1 i value2). Na początku funkcji dopasowujemy do siebie długość obydwu ciągów. Następnie w pętli, począwszy od prawej strony, dodajemy do siebie po kolei cyfry obydwu liczb oraz wartość przeniesienia (zmienna carry) i wynik (zapamiętujemy w zmiennej sum. Nowa wartość przeniesienia carry to suma sum podzielona na 2 (dzielenie całkowite) natomiast do wyniku (zmienna result) dopisujemy z lewej strony, zamienioną na znak, resztę z dzielenia sumy sum przez 2. Po zakończeniu pętli z lewej strony dopisujemy jeszcze wartość przeniesienia carry a na zakończenie, korzystając z funkcji StripLeft(), usuwamy zbędne, początkowe cyfry 0. Dzielimy przez 2, ponieważ jest to podstawa systemu binarnego.



![]() Ćwiczenie 2. Piszemy program dodający dwie liczby zapisane w systemie liczbowym o dowolnej podstawie
Ćwiczenie 2. Piszemy program dodający dwie liczby zapisane w systemie liczbowym o dowolnej podstawie
- Otwórz plik TC2_p1_c2.cpp lub TC2_p1_c2.py. Objaśnij działanie funkcji opisanych w przykładzie 1., korzystając z opisu i kodu podanego. Uruchom program.
- Na bazie funkcji AddBin() zdefiniuj funkcję AddAnyBase() pozwalającą na dodanie dwóch liczb zapisanych w systemie liczbowym o dowolnej podstawie (podstawa systemu powinna być dodatkowym parametrem funkcji).
- Zapisz program w pliku pod nazwą TC2_p1_c2_dowolna_podstawa.cpp lub TC2_p1_c2_ dowolna_podstawa.py
![]() Przykład 2. Odejmowanie liczb dwójkowych
Przykład 2. Odejmowanie liczb dwójkowych
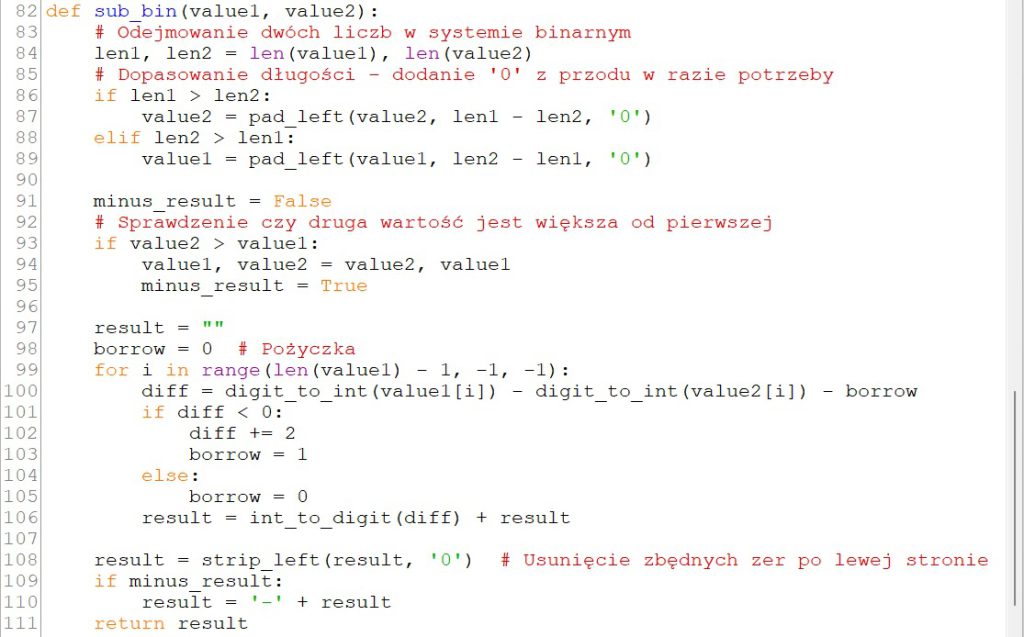
Odejmowanie dwóch liczb zapisanych w systemie binarnym odbywa się w funkcji SubBin(), której parametrami są ciągi value1 (odjemna) i value2 (odjemnik). Na początku funkcji dopasowujemy do siebie długość obydwu ciągów. Następnie porównujemy je leksykalnie (możemy to zrobić, ponieważ ciągi mają teraz taką samą długość) by sprawdzić, czy nie zachodzi przypadek, że odjemnik jest większy od odjemnej. W takiej sytuacji wynik działania będzie liczbą ujemną, ustawiamy zatem wartość zmiennej minusResult na wartość true i zamieniamy miejscami, z wykorzystaniem zmiennej pomocniczej t, wartości value1 i value2. Dzięki temu spełniony będzie warunek value1 >= value2.
Właściwe odejmowanie wykonujemy w pętli. Począwszy od prawej strony, odejmujemy od siebie po kolei cyfry obydwu liczb, pomniejszamy wynik o wartość pożyczki (zmienna borrow) i zapamiętujemy w zmiennej diff. Jeżeli uzyskana wartość jest ujemna, musimy dokonać „pożyczki”. Do wyniku diff dodajemy dwa (podstawa systemu binarnego), a wartość pożyczki ustawiamy na 1. Do wyniku (zmienna result) dopisujemy z lewej strony wartość diff zamienioną na znak. Po zakończeniu pętli, korzystając z funkcji StripLeft() usuwamy zbędne, początkowe cyfry 0 i, jeżeli końcowa wartość ma być liczbą ujemną (zmienna minusResult ustawiona na wartość true), do wyniku dopisujemy znak „-”.



![]() Ćwiczenie 3. Analizujemy program odejmujący dwie liczby dwójkowe
Ćwiczenie 3. Analizujemy program odejmujący dwie liczby dwójkowe
- Otwórz plik TC2_p2_c3.cpp lub TC2_p2_c3.py.
- Objaśnij działanie funkcji odejmującej dwie liczby dwójkowe, korzystając z opisu i kodu podanego w przykładzie 2.
- Uruchom program.
2. Programowanie algorytmów mnożenia i dzielenia na liczbach innych niż dziesiętny
Programowanie algorytmów mnożenia i dzielenia omówimy na przykładzie systemu dwójkowego.
![]() Przykład 3. Mnożenie liczb dwójkowych
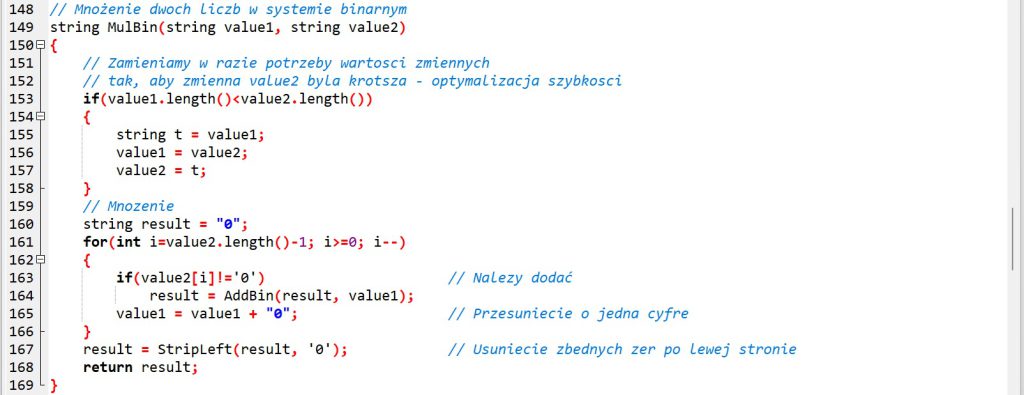
Przykład 3. Mnożenie liczb dwójkowych



![]() Ćwiczenie 4. Analizujemy program realizujący algorytm mnożenia liczb dwójkowych
Ćwiczenie 4. Analizujemy program realizujący algorytm mnożenia liczb dwójkowych
- Otwórz plik TC2_p3_c4.cpp lub TC2_p3_c4.py.
- Objaśnij działanie funkcji odejmującej dwie liczby dwójkowe, korzystając z kodu podanego w przykładzie 3. Omów użyte w funkcji parametry, zmienne, typy danych i instrukcje.
- Uruchom program.
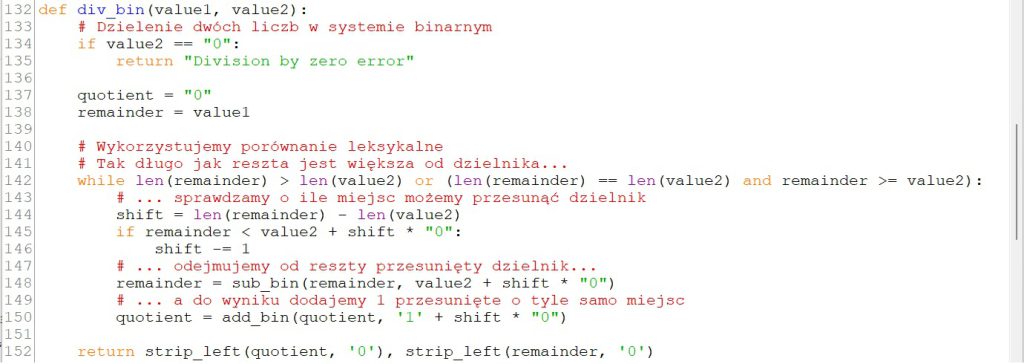
Dzielenie liczb naturalnych x (dzielna) i y (dzielnik) można zrealizować poprzez wielokrotne odejmowanie wartości y od wartości x. Odejmowanie powtarzamy, dopóki pozostała różnica jest większa lub równa y. Liczba wykonanych odejmowań odpowiada wartości dzielenia. Pozostała różnica odpowiada reszcie z dzielenia.
![]() Ćwiczenie 5. Piszemy program dzielący dwie liczby dwójkowe
Ćwiczenie 5. Piszemy program dzielący dwie liczby dwójkowe
- Otwórz plik TC2_p3_c4.cpp lub TC2_p3_c4.py.
- Zdefiniuj funkcję
Div()wykonującą dzielenie dwóch liczb przekazanych jako parametry. - Zapisz program w pliku pod nazwą TC2_p3_c5.cpp lub TC2_p3_c5.py
Wskazówka: Definiując funkcję w języku C++, możesz wzorować się na przykładowym rozwiązaniu w języku Python, pokazanym poniżej:

![]() Zadania
Zadania
- Korzystając z funkcji
DecToAnyBase(), napisz program dodający do siebie binarnie wszystkie możliwe pary liczb naturalnych z przedziału 〈0; 15〉. Skorzystaj z funkcjiAnyBaseToDec()do zweryfikowania, czy dodawania wykonywane jest poprawnie. - Korzystając z funkcji
DecToAnyBase()napisz program odejmujący od siebie binarnie wszystkie możliwe pary liczb naturalnych z przedziału 〈0; 15〉. Skorzystaj z funkcjiAnyBaseToDec()do zweryfikowania, czy odejmowanie wykonywane jest poprawnie. - Korzystając z funkcji
DecToAnyBase()napisz program mnożący przez siebie binarnie wszystkie możliwe pary liczb naturalnych z przedziału 〈0; 15〉. Skorzystaj z funkcjiAnyBaseToDec()do zweryfikowania, czy mnożenie wykonywane jest poprawnie.
Dla zaawansowanych
- Poszukaj w Internecie informacji na temat systemu zapisu liczb BCD (ang. Binary Coded Decimal)

